3.4. решение задачи о кратчайшем пути
3.4. решение задачи о кратчайшем пути
методом динамического программирования
Представленный метод перечисления путей для сложных графов является исключительно громоздким и трудоемким. Гораздо более эффективным методом решения рассматриваемой задачи является метод ДП, к изложению которого мы приступаем.
Пусть v Є v — некоторая вершина графа. Определим функцию l{y) как длину кратчайшего пути, соединяющего вершину у с конечной вершиной г>кон; если такого пути не существует, то функция L считается неопределенной для вершины v. В соответствии с этим определением имеет место равенство L(vKOH) = 0, a L(vHa4) равно длине искомого кратчайшего пути и подлежит определению.
На каждом шаге решения задачи методом ДП множество вершин графа подразделяется на следующие три непересекающиеся группы:
занятые вершины, для которых значения функции L{y) уже вычислены;
пробные вершины, для которых значения функции L{y) еще не вычислены, но имеются оценки E(v) длины кратчайшего пути от v к г>кон (оценки сверху);
свободные вершины, для которых не вычислены ни сами длины L(v), ни их оценки E(v).
В начальный момент решения задачи к занятым вершинам относится только конечная вершина vKOH, а все остальные —к свободным; по ходу решения группа занятых вершин расширяется, а группа свободных — сужается.
Для каждой занятой вершины (за исключением г>КОн) исходящей стрелкой указывается ребро (одно или несколько), в направлении которого следует строить кратчайший путь. Включение в данную группу вершины г>нач означает, что основная расчетная часть алгоритма завершена.
Алгоритм решения задачи о кратчайшем пути методом ДП включает следующие пункты.
Начало работы алгоритма. Полагаем L(vKOH) = 0, вершину vKOH объявляем занятой, а все остальные вершины — свободными.
Проверка. Если начальная вершина г>нач является занятой (т. е. для нее известно значение функции L(y)), то переходим к п. 5.
Вычисление или корректировка оценок незанятых вершин (методика расчетов детально рассмотрена ниже).
Пополнение группы занятых вершин. Из пробных вершин выбираем те, для которых оценки имеют минимальное значение (таких вершин может быть одна или несколько). Эти вершины объявляем занятыми и полагаем для них
L{v) = Е(у).
Переход к п. 2.
Расчет длины кратчайшего пути завершен. Строим кратчайшие пути (один или несколько). Конец работы алгоритма.
Вычисление оценок Е(и) для незанятых вершин и в п. 3 алгоритма проводится следующим образом. Рассмотрим множество всех незанятых вершин графа, каждая из которых является смежной хотя бы с одной занятой вершиной. В это множество могут входить как свободные, так и пробные вершины.
Для свободных вершин оценка вычисляется по формуле
E(u) = min {d(uv) + L(v)},
где минимум выбирается по ребрам вида uv с занятыми вершинами v. Ребро, на котором достигается минимум (таких ребер может быть одно или несколько), отмечается стрелкой, идущей от и к v (от незанятой вершины к занятой).
Для пробных вершин проводится корректировка имеющихся оценок. Если с момента вычисления оценки Е(и) не появилось новых занятых вершин v, смежных с вершиной и, то оценка не меняется. Если же такие вершины появились, то по всем таким вершинам v вычисляется вспомогательный минимум
т = min {d(uv) + L(v)},
аналогичный записанной выше формуле для вычисления оценки. Отметим, что ребер вида uv, для которых вычисленный минимум достигается, может быть одно или несколько. При этом:
если m > Е(и), то оценка не меняется;
если 777. = Е(и), то оценка не меняется, но к установленным ранее стрелкам добавляются стрелки на тех ребрах вида uv, для которых вычисленный минимум достигается;
если 7п < Е(и), то уменьшаем оценку, полагая Е(и) = ттг, установленные ранее стрелки убираем и ставим новые стрелки на тех ребрах вида uv, для которых вычисленный минимум достигается.
Таким образом, в ходе корректировки оценка уменьшается или не изменяется: если обозначить через Е(и) уже имеющуюся оценку, то новая оценка вычисляется по формуле
Е(и) = min {Ё(и), ттг} < Ё(и).
Для удобства контроля ребра, уже учтенные при вычислении оценок, можно отмечать «засечками». При вычислении оценок важно учесть все вершины, смежные с занятыми. Если же незанятых вершин, смежных с занятыми, нет, а начальная вершина все еще не является занятой, то путей, соединяющих заданные начальную и конечную вершины, не существует. В этом случае задача о кратчайшем пути решений не имеет.
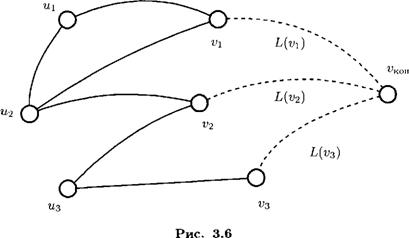
Способ вычисления оценок может быть проиллюстрирован схемой на рис. 3.6. В ней принято, что вершины v,v2,v3 (и, конечно, г>Кон) являются занятыми, причем v и v2 стали занятыми на последнем шаге алгоритма, a v3 стала занятой ранее. Сплошными линиями обозначены ребра графа, пунктирными — кратчайшие пути от занятых вершин к конечной. Среди вершин u,u2,u3, смежных с занятыми, первые две являются свободными, а из является пробной и имеет оценку
Ё(щ) = d(u3v3) + L(v3),
вычисленную с использованием ребра u3d3. В этом случае справедливы формулы
Е(щ) = d(u1v1) + L(v1),
E(u2) = min {d(u2vi) + L(vi), d(u2v2) + L(v2)}, E(u3) = min {E(u3), m}, m = d(u3v2) + L(v2).
Приведенные формулы для вычисления оценок E(u) и длин кратчайших путей L(u) выражают своеобразный аналог классического принципа оптимальности. Эти формулы носят рекуррентный характер, и в них также выделяется первый шаг от текущей вершины и к конечной вершине 1>кон, проводимый по ребру uv при этом длины кратчайших путей от занятых вершин v являются уже известными. Функция L(v) является аналогом семейства функций Беллмана Въ(хг). Расчеты начинаются с конечной вершины и условия L(vKOH) = 0, соответствующего условию -Влг(ждг) = 0. Роль управления играет выбор ребра, по которому следует начинать движение из рассматриваемой вершины. Расчет функций L(y) представляет собой аналог этапа условной оптимизации классического метода ДП.
Построение кратчайшего пути в п. 5 алгоритма представляет собой аналог этапа безусловной оптимизации метода ДП и проводится следующим образом. Начинается построение с начальной вершины г>нач. Из этой вершины выходит по меньшей мере одна стрелка, установленная при вычислении оценок для данной вершины. Переходим по этой стрелке (или по одной из них) в следующую вершину. Аналогично, из этой вершины также выходит по меньшей мере одна стрелка, по которой переходим далее. Так продолжаем до тех пор, пока не придем в конечную вершину 1>кон. При наличии нескольких кратчайших путей все они могут быть построены с помощью алгоритма перечисления путей (см. ниже замечание 4 данного раздела).
Применим рассмотренный метод ДП к решению задачи о кратчайшем пути для заданного на рис. 3.4 графа и выполним подробно все шаги алгоритма, сопровождая решение задачи записью на самом графе (соответствующие расчеты уже представлены на исходном графе рядом с его вершинами).
Полагаем £(Е) = 0, ставим 0 около вершины Е и объявляем данную вершину занятой, а все остальные — свободными.
Поскольку начальная вершина S не является занятой, то переходим к п. 3 алгоритма.
Для занятой вершины Е смежными являются вершины А и Р, причем все они являются свободными, т. е. ни для одной из них оценок еще не рассчитано. Вычисляем оценки впервые для этих вершин:
Е(А) = d(AE) + L(E) = 7 + 0 = 7, Е(Р) = d(PE) + L(E) = 4 + 0 = 4.
Полученные значения записываем на графе около соответствующих вершин, которые переходят в группу пробных вершин. Отмечаем стрелками ребра АЕ и РЕ.
Из двух пробных вершин А и Р значение оценки для вершины Р минимально. Полагаем L(P) — Е(Р) = 4, отмечаем жирным шрифтом данное значение на графе, объявляем вершину Р занятой. Переход к п. 2.
Поскольку начальная вершина S не входит в группу занятых вершин {Е, Р}, то переходим к п. 3.
Для занятых вершин Е и Р смежными являются вершины A, S,T, причем вершины S и Т являются свободными. Вычисляем оценки для этих вершин:
E(S) = d(SP) + L(P) = 9 + 4 = 13, Е(Т) = d(TP) + ЦР) = 6 + 4 = 10.
Полученные значения записываем на графе около соответствующих вершин, которые переходят в группу пробных вершин. Отмечаем стрелками ребра SP и ТР. Отметим, что в настоящий момент впервые рассчитана оценка для начальной вершины S. Для вершины А уже известна оценка Е(А) = 7, рассчитанная ранее, причем после ее вычисления стала занятой только вершина Р, смежная с А. Проводим соответствующую корректировку оценки:
m = d(AP) + L(P) = 1 + 4 = 5.
Поскольку m < Е(А), то полагаем Е(А) = m = 5, и ранее установленную на ребре АЕ стрелку переносим на ребро АР. Полученное значение оценки записываем на графе около вершины А.
Из трех пробных вершин A, S, Т минимальное значение 5 оценка принимает для вершины А. Полагаем L(A) = Е(А) = 5, отмечаем жирным шрифтом данное значение на графе и объявляем вершину А занятой. Переход к п. 2.
Поскольку начальная вершина S не входит в группу занятых вершин {А,Е,Р}, то переходим к п. 3.
В настоящий момент для занятых вершин А, Е, Р смежными являются вершины Н, S, Т, причем вершина Н является свободной. Вычисляем оценку для этой вершины:
Е(Я) = d(HA) + L(A) = 5 + 5 = 10,
записываем полученное значение на графе и переводим ее в группу пробных вершин. Отмечаем стрелкой ребро НА. Для вершин S и Т уже известны оценки E(S) = 13 и Е(Т) = 10, причем только вершина А стала занятой после их вычисления. Корректируем значения оценок:
m(S) = d(SA) + L(A) = 10 + 5 = 15, m(T) = d(TA) + L(A) = 8 + 5 = 13.
Поскольку m(S) > E(S) и m(T) > E(T), то оценки не меняются, и ранее установленные стрелки SP и TP не переносятся.
Из трех пробных вершин Н, S, Т минимальное значение 10 оценка принимает сразу для двух вершин Н и Т. Полагаем
L(H) = Е(Н) = 10, L(T) = Е(Т) = 10, отмечаем жирным шрифтом данные значения на графе, объявляем вершины Н и Т занятыми. Переход к п. 2.
В настоящий момент занятыми являются все вершины графа, кроме начальной вершины S. Переход к п. 3.
Корректируем оценку для вершины S, учитывая, что после ее вычисления стали занятыми две вершины Н и Т:
m = min {d(SH) + L(H); d(ST) + L(T)} = min {2 + 10; 4 + 10} = 12.
Поскольку m < E(S) = 13, то полагаем E(S) — m = 12, ранее установленную на ребре SP стрелку снимаем и переносим на ребро SH, на котором достигается минимум. Полученное значение оценки записывается на графе около вершины S.
Единственной пробной вершиной является вершина S. Полагаем L(S) = E(S) = 12, отмечаем жирным шрифтом данное значение на графе, объявляем вершину S занятой. Переход к п. 2.
Начальная вершина S является занятой. Переход к п. 5.
Основная расчетная часть алгоритма завершена, длина кратчайшего пути равна L(S) — 12. Кратчайший путь строится начиная с вершины S с использованием установленных на графе стрелок SH, НА, АР, РЕ. Таким образом, кратчайший путь имеет вид
S-H-A-P-E.
Конец работы алгоритма.
Полученный результат, конечно, совпадает с результатом, полученным ранее методом перечисления путей.
К решению данной задачи необходимо сделать ряд следующих замечаний.
Замечание 1. В рассмотренном примере значения функции L(y) стали известны одновременно для двух вершин Н и Т; группа занятых вершин пополнилась сразу на две вершины (в отдельных примерах может добавиться и большее число вершин). При этом выпало из рассмотрения ребро НТ, длина 3 которого в расчетах не использована.
Замечание 2. В рассмотренном примере существует только один кратчайший путь. В иных ситуациях может существовать и большее число кратчайших путей. Например, если длину ребра PS изменить с 9 на 8, то возникнет второй кратчайший путь S —Р —Е той же длины 12. Если и длину ребра AS изменить с 10 на 7, то возникнет и третий кратчайший путь S — А — Р Е. При этом после завершения алгоритма из вершины S будет выходить 3 стрелки SA, SH, SP.
Замечание 3. В отдельных случаях значение длины кратчайшего пути может быть получено до того, как будут рассчитаны оценки всех вершин. Например, если длину ребра PS изменить с 9 на 1, то сразу после вычисления L(P) = 4 две вершины А и S получат одинаковые минимальные оценки, равные 5. Это будет означать, что кратчайший путь длины 5 имеет вид S —Р —Е. При этом для вершины Т будет известна только оценка, а вершина Н вообще останется свободной.
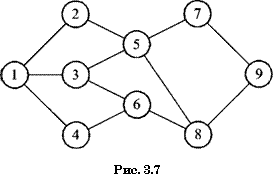 |
Очевидно, что длина кратчайших путей в данном случае равна 4 и совпадает с числом ребер в пути. Расчеты, проведенные методом ДП, приведут к появлению стрелок, указывающих направление построения кратчайших путей, у всех вершин, кроме 9, на всех ребрах в сторону от меньших к большим значениям номеров вершин. Тем самым для построения всех путей необходимо аккуратно рассмотреть все возможные варианты, без пропусков и повторений. Для этого и может служить алгоритм перечисления путей, применение которого даст следующие результаты:
1-2-5-7-9 1-3-5-8-9 1-2-5-8-9 1-3-6-8-9 1-3—5—7—9 1-4-6-8—9
Здесь представлены все 6 кратчайших путей, являющиеся решениями данной задачи.
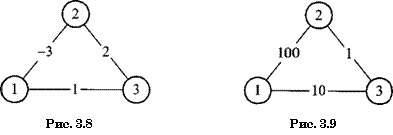
Замечание 5. Важно подчеркнуть, что рассмотренный метод неприемлем для решения задачи о кратчайшем пути на графах, содержащих ребра с отрицательными весами. Для примера рассмотрим граф, изображенный на рисунке 3.8, с начальной вершиной 1 и конечной вершиной 3. В нем имеются 2 пути: 1 — 3 длиной 1 и 1 — 2 — 3 длиной —1, так что кратчайшим является путь 1 — 2 — 3. Формально проводимые расчеты в этом случае дадут:
L(3) = О, Е(1) = 1, Е{2) = 2,
 |
Замечание 6. Подчеркнем, что решить задачу о максимальном пути для графов общего вида с помощью аналогичного алгоритма, заменив в нем формально минимум на максимум, не представляется возможным.
Например, для графа на рис. 3.9 с начальной вершиной 1 и конечной вершиной 3 длина максимального пути 1 — 2 — 3 равна 101. Формально проводимые расчеты дадут:
L(3) = 0, Е(1) = 10, Е(2) = 1,
после чего, следуя желаемой логике, мы должны принять значение L{1) равным 10, что не является верным (здесь функция L есть длина максимального пути к вершине 3).
Замечание 7. Рассмотренный алгоритм предписывает начинать расчеты с конечной вершины и заканчивать начальной вершиной, т. е. вести их в обратном порядке, что соответствует этапу условной оптимизации классического метода ДП; при этом построение кратчайшего пути поводится от начальной вершины к конечной. Важно подчеркнуть, что в теории графов можно изменить порядок расчетов и начинать их с начальной вершины, заканчивать конечной вершиной, а сам кратчайший путь строить начиная с конечной вершины. Соответствующий
алгоритм был разработан в 1959 г. и называется алгоритмом Дийкс-тры по имени выдающегося голландского теоретика и практика программирования второй половины XX в. Эдсгера В.Дийкстры (Edsger W. Dijkstra). В алгоритме Дийкстры занятые вершины называются обычно вершинами с постоянными метками, а пробные вершины — вершинами с временными метками.
Обсуждение Динамическое программирование в экономических задачах
Комментарии, рецензии и отзывы
