8.6. производная неявной функции

8.6. производная неявной функции

Выше было рассмотрено дифференцирование явных функций и параметрических функций. Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y) = 0. Для нахождения производной функции у, заданной неявно, нет нужды искать явное выражение функции у = f(x); нужно просто продифференцировать обе части уравнения, рассматривая у как функцию от ж, а затем из полученного уравнения найти производную у'.

V Пример. Найти производную функции, заданную уравне2 2 x у

нием эллипса —~ Л—7 = 1.

а Ь

Решение. Дифференцируя обе части уравнения, находим: а о

отсюда у

= 2—• Это представление для у' совпадает с фора у

мулой

<> = ±ь-.

а

найденной с помощью явного выражения функции. А

Производная высших порядков

До сих пор мы рассматривали производную ff(x) от функции f(x), так называемую производную первого порядка. Но производная f'(x) сама является функцией, которая также может иметь производную. Производной п-го порядка называется производная от производной (п — 1)-го порядка. Обозначение производных: f"{x) — второго порядка или вторая производная, ffff(x) — третьего порядка или третья производная. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры, например, f(nx), или fIV(x) и т. д.

Выясним механический смысл второй производной. Выше было установлено, что если точка движется прямолинейно по закону s = s(t) (где s — путь, t — время), то s'(to) представляет скорость изменения пути в момент to Следовательно, вторая производная пути во времени s"(to) = [V(to)]' — v'(to) есть скорость изменения скорости или ускорение точки в момент toТеорема о конечном приращении и ее следствия

Теорема Лагранжа. Если функция непрерывна на отрезке [а, Ь] и дифференцируема в интервале (а, 6), то существует такая точка с Є (а, Ь), что

f(b)-f(a) = f'(c)(b-a).

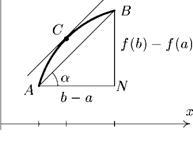
□ Через точки Л(а, f(a)) и B(b, f(b)) данной функции проведем секущую ЛВ (рис. 8.1). Угол, образуемый секущей ЛВ с осью Ох, обозначим через а. Тангенс угла в прямоугольном

а с Ь а с Ь

к теореме Лагранжа к теореме Ролля

Рис. 8.1. Иллюстрации к теоремам Лагранжа и Ролля

треугольнике равен отношению катетов: противолежащего к прилежащему. Из треугольника ABN находим

tga =

BN f(b)-f(a)

AN

Будем перемещать секущую Л В параллельно начальному положению до тех пор, пока она не превратиться в касательную к графику функции у = f(x) в некоторой точке С(с, /(с)), где а < с < b (здесь опускается доказательство того факта, что такое предельное положение существует). Согласно построению и геометрическому смыслу производной tg а равен тангенсу угла наклона касательной /'(с), поэтому

№ /(о) _ fl(A 6-а -J^C>i

а < с <

Отсюда /(6) / (а) = /'(с) (Ь-а).Ш

Следствие 1. Если производная равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная на этом промежутке.

□ Пусть f'(x) = 0 для всех х из данного промежутка. Если а их — две точки этого промежутка, то по доказанной теореме f(x) — f(a) = /'(с) (х — а), а < с < х. Поскольку f'(c) =

О, то

/(я)-/(а)=0, /(ж) =/(а) = const.

5 Я. М. Ахтямов

Следствие 2. Если две функции имеют равные производные в некотором промежутке X, то они отличаются в этом промежутке лишь постоянным слагаемым.

□ Если fi(х) = /2(ж), х Є X, то

{h{x)-f2{x))' = f[{x)-f2{x) = 0.

В силу следствия 1

fi(x) — /2(2?) = const, х Є X. Ш

Прежде чем переходить к формулировке следующей теоремы, напомним, что корнем (или нулем) функции у = f(x) называют такое значение ее аргумента, при котором функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось Ох или касается ее.

Теорема Рол ля. Между двумя различными корнями дифференцируемой функции содержится по меньшей мере один корень ее производной.

□ Пусть а и b — различные корни дифференцируемой функции, т. е. f(a) = 0, f(b) = 0. Из теоремы Лагранжа получаем

/'(с) (6-а) =0, а <с<Ь.

Так как b — а ф 0 (корни различны), то f'(c) = 0. ■

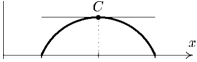
Теорема Ролля имеет простую геометрическую интерпретацию. Между значениями а и b имеется по меньшей мере одно значение с, такое, что в точке С(с, f(c)) графика функции касательная параллельна оси Ох (рис. 8.1).

РОЛЛЬ (Rolle) Мишель (1652-1719) — французский математик, член Парижской Академии наук. В 23 года решил одну из задач, которую не смог до конца решить известный в то время математик Ж. Озанам. Впоследствии чисто алгебраическими средствами для случая многочлена доказал теорему, которая теперь носит его имя. Ролль долгое время критиковал анализ Р. Декарта и исчисление бесконечно малых Г. Лейбница. Хотя эта критика в большинстве случаев была бездоказательной, но она заставила Г. Лейбница внимательнее отнестись к обоснованию основ анализа.

Теорема Коши. Если у = f(x) и у = <р(х) — две функции непрерывные на отрезке [а, Ь] и дифференцируемые в интервале (а, 6), причем (р'(х) ф 0 для любого х Є (а, 6), то между а

и b найдется такая точка с, что

f(b)-f(a) = /'(с^ </?(&)-</? (а) <р'(с)'

Замечание. Знаменатель в левой части равенства отличен от нуля (допустив противное, т. е. (р(Ь) — ср(а), получили бы (р'(с) = 0, что противоречит условию), поэтому выражение в левой части равенства имеет смысл.

□ Введем в рассмотрение функцию

Р(*) = /(,)-/(.)-М^ И*)-*.».

Эта функция удовлетворяет условиям теоремы Ролля. Действительно, во-первых, она дифференцируема в интервале (а, 6), так как дифференцируемы в нем функции f(x) и (р(х):

Во-вторых, F(x) непрерывна на отрезке [а, 6], поскольку непрерывны на нем функции f(x) и <р(х). В-третьих, на концах отрезка [а, Ь] функция F(x) обращается в нуль:

fw = /(.)-/<-)- ш -„(.» = о,

f(») = /(4-«.)-M^M»)-rf.))=0.

Следовательно, между а и b найдется такая точка с, для которой F'(c) = О, т. е.

v ' <p(b)-<p(a) ГУ!

откуда

№ f(a) _ Г (с) ш

(р(Ь)-(р(а) <р'(с)'

С помощью теоремы Коши может быть доказано важное правило, которое позволяет находить пределы дроби f(x) : у?(ж), числитель и знаменатель которой при х —> а стремятся к нулю или бесконечности.

Теорема (правило Лопиталя—Бернулли). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Итак, если имеется неопределенность вида (jj j или (—

то

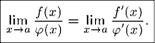
БЕРНУЛЛИ (Bernoulli) Иоганн I (1667-1748) — швейцарский математик, иностранный почетный член Петербургской Академии наук (1725), профессор математики Гронингенского и Базельского университетов. Был деятельным соратником немецкого ученого Г. Лейбница в разработке дифференциального и интегрального исчислений, в области которых им был сделан ряд открытий. Он развил теорию показательной функции, вывел правило раскрытия неопределенностей типа (носящее имя Лопиталя-Бернулли), указал методы

интегрирования рациональных дробей, вычисления площадей плоских кривых, дал определения понятия функции как аналитического выражения и др. В геометрии он дал определение пространственных координат, занимался различными специальными кривыми и др. Ему принадлежат также ценные работы по механике, в частности он дал весьма четкое понятие работы и для простейших случаев сформулировал так называемый «принцип виртуальных скоростей». Среди многочисленных учеников Иоганна Бернулли были такие известные математики как Л. Эйлер, маркиз де-Лопиталь и его сыновья Даниил, Иоганн II, Николай II.

ЛОПИТАЛЬ (Lhopital) Гийом Франсуа Антуан (1662-1704) — французский математик, член Парижской Академии наук. Родился в Париже. Издал первый печатный учебник по дифференциальному исчислению — «Анализ бесконечно малых» (1696). В книге есть правило нахождения предела дроби, числитель и знаменатель которой стремятся к нулю. Это правило теперь называют его именем. Кроме того, он создал курс аналитической геометрии конических сечений. Ему также принадлежит исследование и решение с помощью математического анализа нескольких трудных задач по геометрии и механике.

□ Для простоты рассмотрим доказательство теоремы в случае, когда функции f(x) и (р(х) дифференцируемы в окрестности точки х = а, обращаются в нуль в этой точке и существует предел отношения f'(x) : <р'(х) при х а.

Пусть точка х ф а принадлежит интервалу, в котором функции дифференцируемы. По теореме Коши

f(x)-f(a) _ f'(c) <р(х)-<р(а) <р'(с)' где с лежит между х и а.

По условию f(a) = у? (а), поэтому

№ = Пс)^

<р(х) <р'(с)'

Если х —> а, то с —> а, так как с заключено между х и а. Переходя к пределу в последнем равенстве, получаем

г /(*) г /'(с) r f'(x) ш lim ^4 = lim ^4 = lim ■

х-¥а (рух) с^а ер ус) х-¥а ер ух) sin 2х

V Пример 1. Найти lim :—.

ж->-0 бх — sin х

Решение. При х = О числитель и знаменатель обращаются в нуль, имеем неопределенность вида ^jj^. Применяя правило Лопиталя-Бернулли, получим:

жsin2x /0 le (sin2x)/

lim — = I I = lim —

-+0 Зх — sin ж