9.6. асимптоты графика функции

9.6. асимптоты графика функции

В предыдущих параграфах мы изучали характерные точки. Теперь рассмотрим характерные линии, именуемыми асимптотами.

Вспомним как выглядит знакомый нам график функции у = = —. Нетрудно заметить, что при удалении точки этого графика

x

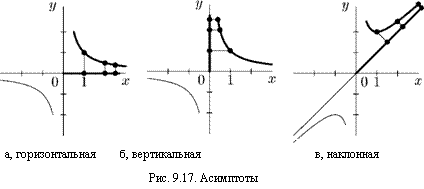
вправо от начала координат расстояние от нее до прямой у = О (оси Ох) стремится к нулю (рис. 9.17, а). В этом случае говорят, что кривая у = 1/х имеет горизонтальную асимптоту у = 0.

При удалении точки графика вверх от начала координат расстояние от нее до прямой х = 0 (оси Оу) также стремится к нулю (рис. 9.17, б). Говорят, что прямая х = 0 является вертикальной асимптотой.

График функции может иметь также и наклонную асимптоту. Таков, например, график функции у = х + 1/х. При удалении точки графика от начала координат расстояние до прямой у = х неуклонно сокращается (рис. 9.17, в).

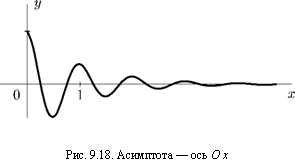
Термин асимптота введен древнегреческим ученым Аполлонием Пергским при изучении гиперболы и происходит от греческого слова «асимтотос», означающего «несовпадающий». Пусть это слово не вводит вас в заблуждение. Асимптоты гиперболы действительно не пересекают график функции (т. е. являются в некотором смысле «несовпадающими»). Однако, согласно современным представлениям об асимптоте, кривая может пересекать свою асимптоту (например, график затухающих колебаний, изображенный на рис. 9.18).

АПОЛЛОНИЙ Пергский (около 260-170 до н.э.) — древнегреческий математик. Его труд «Конические сечения» (в 8 книгах) оказал огромное влияние на развитие астрономии, механики и оптики. Аполлоний ввел понятия и термины: «гипербола», «парабола», «эллипс», «фокус», «асимптота».

Определение. Асимптотой графика функции у = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (ж, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты. График функции у = f(x) при х —> а имеет вертикальную асимптоту, если

lim f(x) = +оо или lim f(x) = —оо;

при этом точка х = а есть точка разрыва. Уравнение вертикальной асимптоты имеет вид

х = а

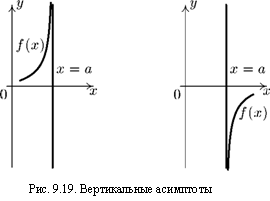(рис. 9.19).

Вертикальные асимптоты х = а следует искать в точках разрыва функции или на концах ее области определения, если концы не равны ±оо.

Горизонтальные асимптоты. График функции у = f(x) при х +оо или х —> — оо имеет горизонтальную асимптоту, если существует и конечен хотя бы один из пределов:

lim fix) = Ьл или lim fix) = 6П.

ж—)— оо х-ї+оо

Если конечен предел 6Л, то говорят, что существует левосторонняя горизонтальная асимптота у = Ьл.

Если конечен предел Ьи, то говорят о существовании правосторонней асимптоты у = ЬП (рис. 9.20).

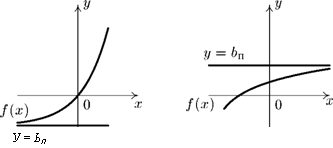левосторонняя правосторонняя Рис. 9.20. Горизонтальные асимптоты

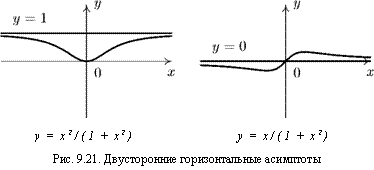
В случае, когда конечные пределы Ьл и 6П совпадают: Ьл = 6П) говорят, что график функции у = f(x) имеет двустороннюю горизонтальную асимптоту у = Ь. Примеры двусторонних горизонтальных асимптот приведены на рис. 9.21.

В том случае, если

lim fix) = оо,

график функции не имеет горизонтальных асимптот, но может иметь наклонные.

Наклонные асимптоты. Наклонной асимптотой графика функции у = f(x) называется ее асимптота, задаваемая уравнением

у = к х + Ь.

Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней, левосторонней и двусторонней.

Теорема. Пусть функция у = f(x) определена при достаточно больших х и существуют конечные пределы

ku = lim , 6„ = lim (f(x)-kx).

ж->-+оо X х^+оо

Тогда прямая у = кПх + Ьп является правосторонней наклонной асимптотой.

□ Если у = ки х + Ьи — наклонная асимптота, то справедливо равенство

Hm {f(x)-(knx + bu))=0 (9.8)

х—>-+оо

и, тем более,

Цт (М-кв-Ь)=0ш

х^+ос X X )

Поэтому

К= lim М.

х-ї+оо X

Теперь из равенства (9.8), учитывая, что к — конечное число, получаем:

Ьи = lim (f(x)-kx). Ш

Аналогично можно показать, что параметры кл и Ьл в уравнении левосторонней наклонной асимптоты у = кл х + Ьл определяются по формулам:

кл= lim , Ьл= lim (f(x)-kJlx).

х^-оо х х^-оо

ки = lim l)u = lim (f(x — kx

x^-oo X x^+oc

бесконечен, то правосторонней наклонной асимптоты график функции у = f(x) не имеет. Аналогично, если кл — оо или Ьл = оо, то левосторонней наклонной асимптоты не существует.

Если кл = ки = к. Ьл = Ьи = b и эти числа конечны, то график функции имеет двустороннюю асимптоту у = к х + Ь.

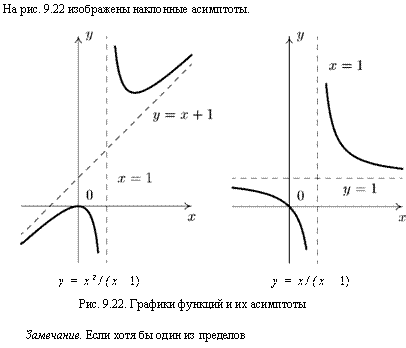
На рис. 9.22 изображена двусторонняя наклонная асимптота у = х + 1.

При отыскании асимптот следует отдельно рассматривать

случаи х ^ а — + а также х —> +оо и —оо.

Горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при к = 0. Поэтому при отыскании асимптот рассматривают лишь два случая: 1) вертикальные асимптоты; 2) наклонные асимптоты.

Схема отыскания асимптот:

для отыскания вертикальных асимптот выписывают все точки разрыва функции и конечные числа на границе области определения функции. Если таких точек нет, то нет и вертикальных асимптот. Если такая точка х = а имеется, то вычисляют пределы:

lim f(x) и lim f(x).

х—>а—0 х—>-а+0

Если хотя бы один из этих пределов существует и бесконечен, то х = а — вертикальная асимптота. Если оба предела не существуют или конечны, то х = а не является асимптотой.

для отыскания правосторонней наклонной (горизонтальной) асимптоты вычисляют пределы:

ku= lim bu = lim (f(x)-kx).

х^+ос х ж->-+оо

Если оба предела существуют и конечны, то прямая у = кп х + Ьп является правосторонней наклонной асимптотой (правосторонней горизонтальной асимптотой, если к = 0). В противном случае правосторонних наклонных и горизонтальных асимптот не существует.

Левосторонние наклонные (горизонтальные) асимптоты находятся аналогично.

V Пример 1. Найти асимптоты кривых:

х

V

X

а) у = —V

б) у =

в) у = . .

Решение.

(если они существуют). Их следует искать среди точек

разрыва функции или на границе ее области определения. Так как функция определена на всей числовой оси за исключением

а) 1) Найдем вертикальные асимптоты графика функции у =

X точки х = 1, то вертикальной асимптотой может оказаться только прямая х = 1. Проверим, является ли прямая х = 1 асимптотой. Для этого вычислим соответствующие пределы:

lim —= (= —оо, lim —= (= +оо.

жчі-о ж 1 -0/ жчі+о ж -1 +0/

Следовательно, кривая имеет вертикальную асимптоту х = 1.

2) Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы:

і і- f(x) і- х і- і ( і ^ гл

А;„ = Inn = lini — — = lini = = U;

ж->-+оо x x^+oc x [X — 1) ЖЧ+ОО I 1 +OC )

bu = lim (fix) — ku x) = lim —-— = lim -——— =

ж->-+оо ж->-+оо x — 1 ж->-+оо x — 1

= lim + —L-Л = 1;

ж->-+оо x — 1 j

кл = lim = lim -r^— = lim -J= f—) = 0;

ж——оо ж жч-оо 1) ж——оо X — i —ОСj

Ьл = lim (/(ж) — кл х) = lim —-— = lim -——— =

ж——оо ж——оо х — 1 ж——оо х — 1

= lim (і + -Ц-) =1,

ж->—оо .7; — 1 j

т. е. у = 1 (у = 0 • ж + 1) — двусторонняя горизонтальная асимптота. Других асимптот нет.

б) 1) Функция определена при всех действительных ж, кроме х = 1. Проверим, является ли прямая х = 1 вертикальной асимптотой. Найдем пределы:

х2 ( 1 ж /1

lim = —— = —оо, lim = —— = +оо.

жЧІ-O I 1 -0/ I 1 +0/

Следовательно, имеется единственная вертикальная асимптота х = 1.

2) Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы:

ки = lim — lim ——— = lim -——— = 1;

ж->-+оо x ж->-+оо x [X — 1) ж->-+оо 1 — 1/X

Ьи = lim (fix) — ku х) = lim ( , — 1 • х ) =

2 _ 2 і

і ф 00 00 I 00 _|

x—>+oc x — 1

&л = lim

ж——ос ж

= lim

ж-)>-ос ж (х — 1) ж-)>-ос 1 — 1/х

= 1;

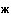
1-а; =

6Л = lim (f(x)-knx)= lim

х—У — оо V Ж — 1

2 _ 2 _|

і ф X X I Ж .j

ж—)— оо Ж — 1

Итак, А;„ = кл = А; = 1 и 6И = 6л = 6 = 1. следовательно, график функции имеет наклонную асимптоту у = х + 1.

в) 1) Функция у =

имеет смысл при всех X Є

лД2 + і

поэтому ее график не имеет вертикальных асимптот. 2) Найдем наклонные и горизонтальные асимптоты:

= lim

ки = lim ^—^ = lim

ж—>-+оо ж ж—>-+оо ^ у/ Xі _|_ ^ Ж^+ОО у/^2 _|_ ^

= 0;

6П = lim (fix) — кп х) = lim — 0 • х ) =

ж->-+оо ж->-+оо л/ж2 _|_ ^ /

= lim —.

ж^+оо у/1 + 1/х

= 1;

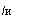&*л = lim

ж—)— ОО X

lim ■

ж^-оо д. у/х2 + !

= 0;

^п = lim (f(x) — кп х) = lim

-°° V лЛ2 +1

Замена ж = — z

-0-х =

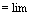= lim

"ОО y/z2 + J Z^-OO д/l + 1/^2

= "І.

Таким образом, при х —> +оо асимптотой служит прямая у = 1 (правосторонняя горизонтальные асимптота), а при х —> —оо — прямая у = — 1 (левосторонняя асимптота). А

V Пример 2. Найти асимптоты кривой у = х3 — Зж. Решение.

Вертикальных асимптот график этой функции не имеет, так как функция у = ж3 — 3 х не имеет разрывов.

f(x)

Найдем пределы lim :

ж->-±оо X

lim Li^l — lim — = lim (х2 — 3) = +оо.

ж—>-±оо х ж—>-±оо х ж—>-±оо

Таким образом, &л = ки = оо. Следовательно, график функции не имеет также наклонных асимптот и горизонтальных асимптот (если бы горизонтальная асимптота существовала имели бы к = 0).

Итак, график функции не имеет асимптот ни вертикальных, ни наклонных, ни горизонтальных. А

Задача. Найти асимптоты графиков функций у = х2, у = = х2/(1 + х2) и у = х/(1 + х2).

Ответ: График функции у = х2 не имеет асимптот. Графики функций у = х21(1 + х2) и у = х/(1 + х2) имеют двусторонние горизонтальные асимптоты, которые изображены на рис. 9.21. (Асимптотой графика функции у = х2/(1 + х2) является прямая у = 1, а асимптотой графика функции у = х/(1 + х2) является ось абсцисс.)