12.7. методы интегрирования
12.7. методы интегрирования
Теорема 1. Если выполнены условия 1) функция f(x) непрерывна на отрезке [а, 6]; 2) отрезок [а, Ь] является множеством значений функции х = g(t), определенной на отрезке а ^ t ^ /3 и имеющую на нем непрерывную производную] 3) д(а) = а, g(fi) = = 6, то справедлива формула:
f(x)dx =
f(g(t))g'(t) dt.
□ Пусть F(x) — первообразная для функции f(x) на отрезке [а, 6], т. е. Ff(x) = f(x) для всех х Є [а, 6], тогда
f(x) dx = F(b) F(a).
Поскольку функции F(x) и х = g(t) являются дифференцируемыми на соответствующих отрезках, сложная функция F(g(t)) дифференцируема и
F't = F'x{x)g't(t) = f{g{t))g'(t).
Следовательно, функция F[g(t)) является первообразной для
функции f(g(t)) на отрезке [a, j3>. По формуле Ньютона-Лейбница получаем
f(g(t))g ) dt = F(g(f3))-F(g(a)) =
= F(b) F(a) =
f(x)dx.
Доказанную формулу называют формулой замены переменной под знаком определенного интеграла. При использовании этой формулы определенного интеграла
f(x)dx
преобразуется с помощью подстановки х = g(t) в определенный интеграл
f(g(t))g'(t) dt
относительно новой переменной t. При этом старые пределы интегрирования а и b заменяются соответственно новыми пределами интегрирования а и /3, которые находятся из исходной подстановки: а = g(a), b = д(/3). При этом нет необходимости, как это было для неопределенного интеграла, возвращаться к исходной переменной интегрирования.
13
V Пример 1. Найти J л/2 х — 1 dx.
Решение. Введем вспомогательную переменную £, связанную с х зависимостью t = 2 х — 1. Дифференцируя, имеем dt =
= 2dx, откуда dx = ^ dt. Находим новые пределы интегрирования. Подставляя в соотношение t = 2 х — 1 значения х = 5 и х = = 13, соответственно получим
« = 2-5-1 = 9,
Следовательно,
/3 = 2-13-1 = 25.
13 25
л/2 х — 1 =
25
I і з
t2 dt=
о
25
= 32-. ▲
При вычислении определенного интеграла методом подстановки принято введение новой переменной, смену пределов интегрирования и другие пояснения записывать в специальных скобках | • | между знаками равенства.
і
V Пример 2. Найти J(2 х3 + 1)4х2 dx.
о
Решение.
(2x6 + l)4x2dx =
t = 2 Xs + 1; dt = 6х2 dx: х2 dx = dt:
6
£ = 1 при ж = 0, £ = 3 при х = 1
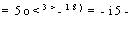 £4 =
£4 =
1 *5 3 1 ,05 l5x ~ 1
6 5
V Пример 3. Найти J —
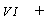
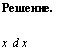
t = у/х + 1; х = t2 1; dx = 2tdt; t = 2 при ж = 3, t = З при ж = 8
(Г -l)2tdt
= 2
(Г 1) dt = 2 ( t
о
= 2 (9 3) 2 (I 2) = 10|. A
тг/2
Задача 1. Найти J sin3 ж of ж.
Ответ: (подстановка t = cos ж), о
Рассмотрим теперь, как выполняется интегрирование по частям в определенном интеграле.
Теорема 2. Пусть функции и = и(х), v = v(x) имеют непрерывные производные на отрезке [а, Ь]. Тогда
| Ь | Ь | ||
| ■* | ъ | ||
| и dv = uv | — | v du, | |
| а | |||
| а | а | ||
где и v
= u(b) v(b) — и (a) v(a).
Эта формула называется формулой интегрирования по частям для определенного интеграла.
□ Поскольку (и v)f = и1 v + и Vі, функция и v является первообразной для функции и' v + и Vі. Тогда по формуле Ньютона-Лейбница и свойству 2 получаем:
и v
(и v + и Vі) dx =
v и dx +
uv' dx =
v du +
и dv.
тг/2
V Пример 4. Найти J х cosxdx.
о
Решение.
тг/2
х cos х dx =
и = х: du = dx;
dv = cos ж б/ж;г> = sin х
= х sin X
тг/2 О тг/2
sin ж = — sin — — U + cos х
тг/2 О
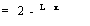 | |||
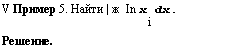 | |||
х In ж dx =
и = In х du = (In x)'dx = — dx; dv = х dx:v = —
х
= Y x
— • — dx = (х1 In x — x1
2 x
Задача 2. Найти J ж In2 ж of ж.
Ответ: і (е2 — 1) — интегрирование по частям производится дважды.
Примеры вычисления неопределенных интегралов с помощью пакета символьных вычислений Maple уже приводилось в этой книге. С его помощью можно вычислять и определенные интегралы. Покажем как выглядит решение примера 5 и задачи 2 с помощью компьютера:
>int(x*ln(x),х=1..ехр(1));
1 2 1 4Є +4
>int(x*(ln(x))~2,x=l. .exp(l)) ;
4 4*
Конечно же для таких простых примеров нет необходимости в применении компьютера. Компьютер целесообразно использовать в случае, когда требуется выполнение рутинных вычислений. Так, вычисление определенного интеграла
х In10 х dx
требует выполнения десяти интегрирований по частям. Такую задачу лучше поручить компьютеру. Она легко найдет ответ:
>int(x*(ln(x))'410,x=l. .exp(l));
1919 о 14175
—е •
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
