Глава 15 оптимизационные задачи 15.1. экстремум функции двух переменных

Глава 15 оптимизационные задачи 15.1. экстремум функции двух переменных

Внутренняя область каждого круга с центром Pq(xq, Уо) и радиусом 8 > О называется окрестностью точки Ро(жо? уо).

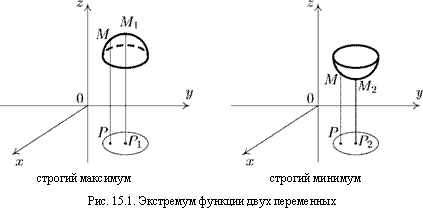
Рассмотрим функцию z = /(ж, у), непрерывную в окрестности точки Pi (х, у). Строгим максимумом [строгим локальным максимумом) функции z = f(x, у) называется такое ее значение /(#i,yi), которое больше всех других значений, принимаемых в точках Р(ж,у), достаточно близких к точке Рі(жі,уі) и отличных от нее (рис. 15.1), т. е.

/(жьуі) > f(x, у).

Пусть функция z = /(ж, у), непрерывна в окрестности точки ^2(^2,2/2)Строгим минимумом (строгим локальным минимумом) функции z = f(x, у) называется такое ее значение f(x2^y2) в точке Р2(х2^ 2/2)5 которое меньше всех других значений, принимаемых в точках Р(ж, у), достаточно близких к точке Р2(х2^ у2) и отличных от нее (рис. 15.1), т. е.

/(ж2, Уі) < f(X' У)Если рассмотренные выше неравенства являются нестрогими, то говорят о нестрогих локальных максимуме и минимуме соответственно.

В случаях, когда упоминание о том, является ли максимум или минимум строгим или нестрогим, локальным или глобальным, не является существенным, то соответствующие прилагательные опускают.

Точки максимума и минимума называются точками экстремума.

Приведем теоремы, облегчающие нахождение экстремумов функции двух переменных.

Теорема 1 (необходимое условие экстремума). Если функция z = f(x, у) имеет в точке Ро(хо, уо) экстремум и первые частные производные f'x(xo, у о), /^(жо, у о) непрерывны в некоторой окрестности этой точки, то

Ґх(х0і Уо) = 0, /у(жо, Уо) = 0. (15.1)

□ Если в точке (жо, Уо) функция / (ж, у) имеет максимум, то функция / (ж, уо) одной переменной ж имеет в точке ж = жо максимум, и, следовательно, ее производная ffx(xo, уо) равна нулю. Функция /(жо, у) одной переменной у также имеет в точке у = = уо максимум, и, следовательно, ее производная /^(жо, Уо) равна нулю. Следовательно, одновременно должно иметь место:

fx(xo, Уо) = 0, /у(ж0, Уо) = 0.

Аналогично доказывается случай, когда функция /(ж, у) имеет в точке (жо, Уо) минимум. ■

Точки, при которых выполняются (15.1), называются стационарными точками функции z = /(ж, у).

Теорема 2 (геометрический смысл необходимых условий экстремума). В стационарной точке касательная плоскость к поверхности z = f(x, у) параллельна плоскости хОу.

□ Пусть Ро(#(ьУо) есть стационарная точка функции z = f(x,y). Уравнение касательной плоскости в этой точке имеет вид

z z0 = z'x(x0, г/о) (х ~ хо) + z'y(x0, г/о) (у ~ Уо)Так как частные производные равны нулю, то получаем

Z — Zq — 0, Z = Zo. Ш

Заметим, что точки экстремума могут быть не только в тех точках, в которых частные производные функции равны нулю. Экстремум функции может быть и в тех точках, где хотя бы одна из частных производных не существует или равна бесконечности. На рис. 15.2 изображена функция с конусообразным графиком. В вершине конуса — точке М — находится максимальная точка функции, однако частные производные там не существуют (в соответствующей точке невозможно провести касательную плоскость) .

Более того, обращение в нуль или же несуществование частных производных первого порядка является более общим необхо-димымым условием экстремума.

конус седловина

Однако это необходимое условие недостаточно для существования экстремума. Например, у седловидной поверхности z = х2 — г/2, изображенной на рис. 15.2, частные производные равны нулю в точке M<i, но эта точка не является экстремумом.

Теорема 3 (достаточные условия экстремума). Если функция z = f(x, у) имеет в окрестности точки Po(xq, уо) первые и вторые непрерывные частные производные, то в точке Ро, в которой выполняются необходимые условия (15.1), имеет место экстремум в случае, когда в этой точке

А = f'L ■ f'y (Ґ:У)2 > 0. (15.2)

Функция имеет максимум в точке Ро(хо, уо), если в этой точке ffxfx < 0; и минимум, если fxx > 0.

Если же А < 0, то функция z = f(x, у) не имеет экстремума в точке Ро.

Таким образом, схема исследования функции z = f(x, у), имеющей непрерывные первые и вторые частные производные, на экстремум такова. Вначале сужаем область поиска. Находим стационарные точки (только они могут быть точками экстремума). Далее, пусть Ро(хо, уо) является стационарной точкой функции. Значения производных второго порядка в точке Ро обозначим так:

f"x(x0i Уо) = А', f"y(x0i Уо) = В; fyy{xo, Уо) = С.

Составим определитель

Д =

Л в в с

= AC -Bz

Если А < 0, то в стационарной точке Ро нет экстремума (в этом случае Ро является так называемой седловиной, или точкой минимакса; рис. 15.2).

Если А > 0, то в точке Ро есть экстремум, причем максимум, если Л < 0, и минимум, если Л > 0.

Если А = 0, то требуется дополнительное исследование. (В этом случае возможны оба случая. Для одних функций в стационарной есть экстремум, для других — нет.) Поэтому при А = 0 проводят исследование, используя определение.

V Пример 1. Найти экстремум функции z = 2х + 8у х2 2у2.

Решение. Находим частные производные функции:

4 = 2-2ж, 4 = 8-4у.

Находим стационарные точки. Для этого решаем систему уравнений

zx = 2 2х = 0, ^ = 8 4у = 0,

откуда х = 1, у = 2. Таким образом, стационарной является точка Ро(1, 2). Находим значения частных производных второго порядка в точке Pq:

А = 4Х(Р0) = -2, В = 4ДР0) = -4, С = 4у(Р0) = 0.

Составляем выражение

А = АС В2 = (-2) • (-4) О2 = 8.

Так как А > 0 и А < 0, делаем вывод о наличии максимума в точке Ро(1, 2). При этом минимальное значение функции равно

\%т'т — 9. А

V Пример 2. Найти экстремум функции

z = 2 Xs + х у2 + 5 х2 + у2 + 1.

Решение. Находим частные производные функции:

z'x = 6 х2 + у2 + 10 ж, ^ = 2 ж у + 2 у.

Находим стационарные точки. Для этого решаем систему уравнений

z'x = 6 х2 + у2 + 10 х = 0, z'y = 2xy + 2y = 0. Решение системы дает 4 стационарные точки:

Л(0,0), Р2(~,0), Р3(-1, 2), Р4(-1, -2).

Находим значения частных производных второго порядка:

zxx — 12 ж + 10; zXy = 2 у] Zyy = 2 х + 2.

Исследуем каждую стационарную точку.

1) В точке Рі(0, 0): А = 10; В = 0; С = 2; А = 20. Так как А>0иЛ>0, то в этой точке функция имеет минимум:

Zmm = z(0, 0) = 1.

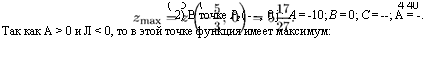В точке Р3(-1, 2): Л = -2; В = 4; С = 0; А = -16. Так как А < 0, то в этой точке нет экстремума.

В точке Р4(-1, -2): А = -2; 5 = -4; С = 0; А = -16. Так как А < 0, то в этой точке нет экстремума. А

Задача. Найти экстремум функции

z — 3 х + 6 ;/у — Xі — х у — у2.

Ответ: zmax = я(0, 3) = 9.

В следующей главе будет рассмотрено приложение этого материала к задачам на экономию ресурсов.

15.2. Экстремум функции многих переменных

Достаточные условия экстремума функции можно сформулировать и на языке квадратичной формы, изучаемой в разделе «Аналитическая геометрия и линейная алгебра». Достаточные условия экстремума функции многих (и не только двух) переменных сводятся к положительной (или отрицательной) определенности квадратичной формы

п

ЛікАхіАхк,

і,к=1

где А{к — значение ffxfiXk в исследуемой точке.

Прежде чем сформулировать соответствующие теоремы приведем некоторые сведения из о квадратичных формах.

Некоторые сведения о квадратичных формах. Функция вида

п

^ ^ &ік \%і \% к і,к=1

называется квадратичной формой от переменных х, х<і, ..., хп; коэффициенты не зависят от Х, Х2, ..., хп.

Если = аы Для всех i, k = 1, 2, ..., п, то квадратичная форма называется симметричной.

Симметричная квадратичная форма от переменных жі, Ж2,..., хп называется положительно определенной (отрицательно определенной), если она имеет положительные (отрицательные) значения при всех значениях переменных жі, x2l ..., не равных одновременно нулю.

V Пример 1. Проверить положительную определенность формы

6 х + 5 х + 14 х + 4 х Х2 — 8 х х\% — 2 х2 х\%.

Решение. Форму можно представить в виде

(2 хх 3 х3)2 + 2(Х1 + х2 + х3)2 + 3 (х2 х3)2.

Следовательно предложенная для проверки квадратичная форма является положительно определенной. А

Положительно определенные и отрицательно определенные квадратичные формы объединяют под названием знакоопреде-ленных форм.

Если симметричная квадратичная форма имеет как положительные, так и отрицательные значения, то она называется знакопеременной.

V Пример 2. Показать знакопеременность формы

6 х + х + х + 8 х Х2 — 8 х х\% — 2 х2 жз 

Решение. Значение формы равно +6 при х = 1, х2 = х\% = = 0 и равно —1 при х = 1, х2 = —1, х\% = 0. Следовательно, предложенная для проверки квадратичная форма принимает как положительные, так и отрицательные значения и поэтому является знакопеременной. А

Сформулируем критерий знакоопределенности симметричной квадратичной формы. Будем называть матрицу

		0>12 •	• din
at/fe|| =	а>21	«22 •	• &2п
	0"п1	&п2 •

матрицей квадратичной формы

п

Ф = ^2 ciikXiXk, аік = акі, і, k = 1,2, i,k=l

Определители этой матрицы

П.

Ді = ац, Д2 =

«21 «22

An =

an аіг

«21 «22

«ln «2n

«nl «n2

a.

называются главными минорами матрицы ||«г/с|| квадратичной формы Ф.

Критерий Сильвестра. Для того чтобы симметричная положительная форма была положительно определенной, необходимо и достаточно, чтобы выполнялись условия

Ai > О, А2 > О,

Ап > 0.

Для того чтобы симметричная квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров

Аь Д2, Ап

чередовались, причем

Ах < 0.

СИЛЬВЕСТР (Sylvester) Джеймс Джозеф (1814-1897) английский математик, член Лондонского королевского общества. Родился в Лондоне. Важнейшие работы Сильвестра относятся к алгебре, теории чисел, теории вероятностей, механике и математической физике. Он заложил основы теории элементарных делителей двух квадратичных форм, развил теорию канонических форм, т. е. разрешил задачу сведения формы к простейшему виду. Ему принадлежат все термины этой теории: инвариант, ковариант, коммутант, дискриминант и т. д. Вообще, он ввел очень много употребляемых в современной математике терминов. Учреждена медаль им. Сильвестра.

V Пример 3. Проверить знакоопределенность форм 6 х + 5 х + 14 х + 4 х Х2 — 8 х х\% — 2 х2 х\%

6 х + х + х + 8 х Х2 — 8 х х\% — 2 х2 х\% из примеров 1 и 2 по критерию Сильвестра.

откуда

Ai = ац = 6 > О, Д2 =

«12 «13 «22 «23 «32 «33

«21

азі

Решение. Для формы из первого примера имеем ац = 6,

Поскольку все главные миноры положительны, то квадратичная форма из примера 1 является положительно определенной.

Ai = ап = 6 > О, А2 =

= -10 < 0.

Два главных минора квадратичной формы из примера 2 удовлетворяют неравенствам

«11 «12 _ 6 4 «21 «22 4 1

Поэтому соответствующая квадратичная форма не может быть положительно определенной или отрицательно определенной. Следовательно она является знакопеременной. А

Рассмотрим теперь как с помощью квадратичных форм находить точки экстремума.

Достаточные условия экстремума. Отметим, что окрестность, минимум, максимум и экстремум для функции многих переменных определяются аналогично тому, как это сделано для функции двух переменных. Так же как и в случае функции двух переменных, доказывается

Теорема 1 (необходимое условие экстремума). Если функция z = /(жі, Ж2, ... , хп) имеет в точке Pq экстремум и первые частные производные ffx , і = 1, 2, ..., п непрерывны в некоторой окрестности этой точки, то

/' =0, і = 1, 2,

Ро

п.

(15.3)

Точки, в которых выполняются условия (15.3), называются стационарными.

Необходимое условие экстремума может быть сформулировано и в терминах дифференциалов.

Введем для этого необходимые определения.

Полный дифференциал функции многих переменных, который называют еще и дифференциалом первого порядка вводится по аналогии с полным дифференциалом функции двух переменных.

Пусть функция z = /(жі, Ж2, ...,хп) имеет непрерывные частные производные zx±. Дифференциалом первого порядка такой функции называется выражение dz, которое вычисляется по формуле

dz = ZX! Лж1 + zx2 Лж2 + ••• + z'Xn Axn.

Дифференциалы независимых переменных совпадают с их приращениями, т. е. dx{ = Ахі.

Из условий (15.3) вытекает, что в точке локального экстремума

dz	= 0.
	Ро

(15.4)

Обратное утверждение также верно: если в точке Ро первый дифференциал функции z = /(жі, Ж2, ... , хп) тождественно равен нулю (как функция относительно dxi), то все частные производные z'x в указанной точке также равны нулю в силу произвольности dx{.

Условия (15.3) или (15.4) не являются достаточными условиями экстремума.

Достаточное условие экстремума формулируется с помощью привлечения второго дифференциала функции.

Пусть функция z = /(жі, #2, ••• -> хп) имеет непрерывные частные производные zx. Xk. Дифференциалом второго порядка этой функции называют выражение

п

d z = *У ] zx. Xk dx dxf*.

і, k=l

Здесь дифференциалы независимых переменных совпадают с их приращениями, т. е. dx = Ахі, dx= Аж^.

Нетрудно видеть, что дифференциал d2z представляет собой симметричную квадратичную форму относительно дифференциалов независимых переменных dx, dx2l dxn. Матрица этой квадратичной формы, элементы которой являются вторыми

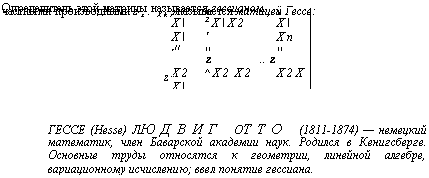Теорема 2 (достаточные условия экстремума). Пусть в стационарной точке Ро и в некоторой ее окрестности функция z = f(x, Ж2, ... , хп) имеет все непрерывные частные производные. Тогда, если в этой точке второй дифференциал d2z является знакоопределенной квадратичной формой от дифференциалов dx, dx2, dxn независимых переменных, данная функция имеет в точке Ро локальный экстремум. При этом

если d2z является положительно определенной квадратичной формой, то функция z = f(x, x<i, ... , хп) имеет в точке Ро локальный минимум;

если d2z является отрицательно определенной квадратичной формой, то функция z = f(x, Ж2, ... , хп) имеет в точке Ро локальный максимум.

Если же d2z является знакопеременной квадратичной формой, то функция z = f(x, Ж2, ... , хп) не имеет локального экстремума в точке Ро.

V Пример 4. Найти экстремум функции трех переменных z = х + х + х2.

Решение. Найдем стационарную точку функции. Для этого приравняем первые частные производные к нулю:

z'Xl =2xi = 0, zX2 = 2x2 = 0, zX3 = 2 xs = 0.

Отсюда получаем единственную стационарную точку 0(0,0,0). Проверим, является ли эта точка точкой экстремума. Найдем вторые частные производные.

" = о z" =2 z" =2

Х2 ' Х жз u5 ^ж2 жз u*

Гессиан, составленный из этих вторых частных производных в точке О(0, 0, 0), имеет вид

2 0 0 0 2 0, 0 0 2

все главные миноры

Ах = 2, А2 = 4, А3 = 8

которого положительны. Следовательно, согласно критерию Сильвестра, квадратичная форма d2z положительно определена. Поэтому из теоремы 2 вытекает, что функция z = х + х + х имеет в точке О(0, 0, 0) локальный минимум. А

Отметим, что теорема 3 (о достаточных условиях экстремума функции двух переменных) из предыдущего пункта является следствием теоремы 2, поскольку введенный в предыдущем пункте определитель А является гессианом функции двух переменных.

15.3. Отыскание наибольшего и наименьшего значений функции двух переменных в заданной замкнутой области

Пусть требуется найти наибольшее и наименьшее значение функции z = f(x, у) в некоторой замкнутой области D. Этих значений функция достигает либо во внутренних точках области, которые являются стационарными точками функции, либо на границах области. Следовательно, чтобы найти наибольшее и наименьшее значение функции в заданной области, необходимо:

найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки нет необходимости;

найти наибольшее и наименьшее значение функции на границе области; если граница области состоит из нескольких линий (участков), то исследование проводится для каждого участка в отдельности;

сравнить все полученные значения функции; наибольшее из них будет наибольшим, а наименьшее — наименьшим значением функции в заданной области.

V Пример. Найти наибольшее и наименьшее значение функции z = x2 + 2y2-2x-\%y + §v замкнутом треугольнике АО В, ограниченном осями координат и прямой х + у — 4 = 0 (рис. 15.3).

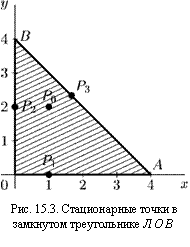Решение. Найдем стационарные точки:

4 = 2ж-2; 4 = 4 у 8.

Решая систему

4 = 2 ж 2 = 0;

4 = 4у-8 = 0,

находим стационарную точку

Ро(1, 2). Эта точка лежит внутри области. Вычислим значение функции в этой точке:

z(PQ) = z(l, 2) = 1 + 8 2 16 + 5 = -4.

Граница заданной области состоит из отрезка OA оси Ох, отрезка О В оси О у и отрезка А В. Определим наибольшее и наименьшее значения функции z на каждом из этих трех участков. На отрезке OA имеем у = 0, 0 ^ х ^ 4. При у = 0 функция

2 = ж

2х + 5

есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке [0, 4]:

dz dx

= 2х-2- 2ж-2 = 0; х = 1;

Pi(l, 0) — стационарная точка. Значение функции в этой точке равно z(Pi) = z(l, 0) = 4.

Вычислим значения функции на концах отрезка О Л, т. е. в точках О и А:

z(0) = *(0, 0) = 5; z(A) = z(4, 0) = 13.

На отрезке О В имеем х = 0 и 0 ^ у ^ 4. При ж = 0

* = 2у2-8у + 5.

Находим наибольшее и наименьшее значение этой функции z от переменной у на отрезке [0, 4]:

4=4у-8; 4^-8 = 0; у = 2;

^2(0, 2) — стационарная точка,

z(P2) = z(0, 2) = -3.

Вычислим значения функции z на концах отрезка 05, т. е. в точках О и В:

z(0) = *(0, 0) = 5, z(B) = *(0, 4) = 5.

Исследуем теперь отрезок ЛВ. Уравнение прямой А В:

у = 4 — х.

Подставив это выражение для у в заданную функцию z, получим z = х2 + 2 (4 х)2 2 х 8 (4 х) + 5,

или

z = 3х2 -10х + 5.

Определим наибольшее и наименьшее значения функции на отрезке [0, 4]:

5

z'x = 6 х — К): 6 х — К) = 0: х = -; Н\% I -, I — стационарная точка,

3' 3

Значения в точках А и В найдены ранее. Сравнивая полученные результаты, заключаем, что наибольшее значение заданной функции z в заданной замкнутой области достигается в точке А(4, 0), а наименьшее значение — в стационарной точке Ро(1? 2). Таким образом, наибольшее значение достигается в точке 2(4, 0) = 13, а наименьшее — в точке z(l, 2) = —4. А

Задача. Найти наибольшее и наименьшее значения функции

Z = X2--y2-Xy--X--y

в замкнутом треугольнике, ограниченном осями координат и прямой

х + у + 3 = 0.

Ответ: Наименьшее значение: —1, а наибольшее: 6.

В следующей главе рассмотрено приложение методов поиска наибольших и наименьших значений функций к задачам повышения урожайности.