§ 3.2. продуктивные модели леонтьева

§ 3.2. продуктивные модели леонтьева

Определение. Матрица А>0 называется продуктивной, если для любого вектора J> S 0 существует решение х > 0 уравнения

х = Ах+у. (3.4)

В этом случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.

Итак, модель Леонтьева продуктивна, если любой вектор у й 0 конечного потребления можно получить при подходящем валовом выпуске х > 0.

Нижеследующая теорема 1 показывает, что нет необходимости требовать существования решения х > 0 уравнения (3.4) для любого вектора у>0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора у > 0.

Условимся в дальнейшем писать у>0 и называть вектор у положительным, если все компоненты этого вектора строго положительны.

Теорема 1 (первый критерий продуктивности). Если А S 0 и для некоторого положительного вектора у* уравнение (3.4) имеет решение х*^. 0, то матрица А продуктивна.

Заметим, что на самом деле х*> 0, что следует из х*= Ах*+у* и А >0, х*>0, J*>0.

Доказательство теоремы не приводим. Уравнение Леонтьева (3.4) можно записать следующим образом:

(Е-А)х = у, (3.5)

где Е — единичная матрица. Возникает, естественно, вопрос об обращении матрицы Е-А.

Понятно, что если обратная матрица {Е-А)~{ существует, то из (3.5) вытекает

х = (Е-А) у. v 5" 67

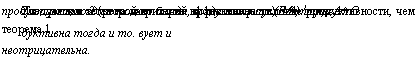Доказательство. Если (Е-А)'1 существует и > 0, то из формулы (3.6) следует продуктивность матрицы А.

Обратно, пусть матрица А продуктивна. Рассмотрим следующие системы уравнений:

(Е А) х = ё,, (Е А) х = ёг,..., (Е А) х = ёЛ,

где ех, ё2> ё„ — столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т. е. существуют такие векторы (столбцы) С| £ 0, с2 £ 0,сп £ О, что

(Е-А)с1=ё1, (Е-А)с2 = ё2 (Е-А)с„ = ёп. (3.7)

Обозначим через С матрицу, составленную из столбцов сх с2, сп. Тогда вместо п равенств (3.7) можно написать одно:

(Е-А)С = Е.

Следовательно, матрица (Е-А) имеет обратную С, причем С>0. Теорема доказана.

Пр им ер 1. Исследуем на продуктивность матрицу

(0,2 0,6 Л " |^0,9 0,3

А =

В данном случае

f 0,8 -0,6

-0,9 0,7

Необходимые вычисления предоставим читателю провести самостоятельно. Получаем матрицу (Е-А)~которая существует и равна

'35 30Л 45 40

Мы видим, что эта матрица неотрицательна. Следовательно, А продуктивна. 68

Продолжим анализ продуктивности модели Леонтьева. Пусть а — некоторое число. Из курса математического анализа известно, что если ряд

1 + а + а2 + ...

(бесконечная геометрическая прогрессия) сходится (условием этого

является а < 1), то его сумма равна (1-а)-1. Убедимся, что аналогичное предложение имеет место при замене числа а матрицей А.

Лемма. Если бесконечный ряд (из матриц)

1+А+А2 + ... (3-8)

сходится, то его сумма есть матрица (Е-А)~1.

Доказательство. Пусть ряд (3.8) сходится. Прежде всего покажем, что матрица (Е-А) имеет обратную матрицу.

Рассуждая от противного, допустим, что матрица (Е-А) — вырожденная. Рассмотрим тождество

(Е + А +A2 + ...+Ak~l) (Е-А) = Е-Ак. <3-9)

Мы знаем (§ 2.9), что уравнение Вх = 0 с вырожденной матрицей В обязательно имеет ненулевое решение. Следовательно, существует вектор х * 0,такой, что (Е-А)х = 0. Применив к вектору х обе части равенства (3.9), получим (Е-Ак)х = 0 или х = Ак х. Но ІітАк = 0, что

следует из сходимости ряда (3.8) (необходимое условие сходимости

ряда). Следовательно, lim Ак х = 0, т. е. х = 0 вопреки условию.

к-*со

Таким образом, матрица Е-А имеет обратную матрицу. Из (3.9) находим

Е + А+А2 + ...+Ак~] = (Е-Ак) (Е-А)' С учетом того, что imAk = 0, получаем

1іт(Е + Л +A2 + ...+Ak~l) = (E-ATl.

к-*<а

Итак, сумма ряда (3.8) существует и равна (Е-А)~'. Лемма доказана.

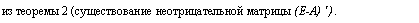Теорема 3 (третий критерий продуктивности). Матрица А>0 продуктивна тогда и только тогда, когда сходится бесконечный ряд

Е + А+А2 + ... (3-Ю)

Доказательство. Пусть сходится ряд (3.10). Согласно лемме его сумма равна (Е-А)~1. При этом сумма указанного ряда будет S 0, поскольку все слагаемые ряда неотрицательны. Итак,

матрица (Е-А)~ существует и неотрицательна. Отсюда по теореме 1 следует продуктивность А.

Обратное утверждение (если А продуктивна, то ряд (3.10) сходится) доказывать не будем.

Полученный нами критерий продуктивности матрицы А (сходимость ряда (3.10)) в ряде случаев может быть использован для проверки матрицы А на продуктивность. Покажем, например, что если сумма элементов любого столбца неотрицательной матрицы А меньше 1 , то А продуктивна. Действительно, пусть q — наибольшая из указанных сумм, q < 1. Ясно, что тогда все элементы матрицы А не превосходят q. Из правила перемножения матриц легко вывести, что любой элемент матрицы А2 не превосходит q2:

{А = аЛ а у + ап a2j + ... + ain anj < q (an + ... + < q2.

Точно так же получим, что элементы матрицы Л3 не превосходят а3 и т. д. Отсюда следует сходимость ряда (3.10), а значит,и продуктивность матрицы А.

Пр имер 2. Для матрицы

fo,i о 0,6

А = 0,2 0,7 0 0,4 0,2 0,3

сумма элементов каждого столбца меньше единицы. Следовательно, А продуктивна.

Аналогично доказывается, что если в неотрицательной матрице А сумма элементов любой строки меньше 1, то матрица А продуктивна. Впрочем, то же самое можно вывести и из следующего предложения: если продуктивна матрица А, то продуктивна и матрица А Т, что следует из теоремы 2.

Пусть А^.0 — продуктивная матрица. Запасом продуктивности матрицы А назовем такое число а>0, что все матрицы ХА, где 1 < X < 1+а, продуктивны, а матрица (1-ш.)А — не продуктивна.

Пример 3. Выясним, какой запас продуктивности имеет матрица А из примера 1.

Решение. Будем руководствоваться критерием продуктивности

( 1-0,2*, -0,6* -0,9* 1 0,3*

теоремы 2 (су В данном случае

Е-ХА = Определитель этой матрицы

Д = Е ХА = (1-0,2Х) (1-0,3) 0,542 = 0,482 0,5 + 1. Обратной матрицей будет

(Е-ХА)'1 =

1-0,3 0,6

Д Д

0,9 1-0,2

А Д

Для продуктивности матрицы ХА нужно, чтобы все элементы обратной матрицы были неотрицательны. Это возможно лишь если Д > 0, 1-0,2 > 0, 1-0,3 > 0. Приближенные корни уравнения Д = 0 суть , =-2,06 и 2= 1,015, поэтому (Е-ХА)~1 >0 » <1,015. При * < 2 матрица ХА будет продуктивной, при = 2 — нет. Запас продуктивности матрицы А равен 0,015. Мы видим, что матрица А находится где-то «на пределе» продуктивности.

Обычно матрицы А межотраслевого баланса обладают большим запасом продуктивности. Например, для межотраслевых балансов в бывшем СССР такой запас, как правило, был больше 0,4. Рост производственных расходов (в частности, учет затрат на преодоление негативных воздействий производства на окружающую среду) вызывает увеличение элементов матрицы/} и, как следствие, снижение ее запаса продуктивности.