§ 5.2. применение метода наименьших квадратов

§ 5.2. применение метода наименьших квадратов

Метод наименьших квадратов широко используется при анализе статистических данных для выявления функциональной зависимости между наблюдаемыми величинами. Для применения метода наименьших квадратов количество наблюдаемых величин не имеет принципиального значения. Однако, поскольку нашей задачей является знакомство с методом, а не изложение теории анализа данных, мы ограничимся случаем, когда наблюдаются всего две величины х и у, между которыми предполагается наличие функциональной связи у = Р(х), где

Р(х)=Р0 +РХ +/>22 + +Pkxk — многочлен степени к.

ПуСТЬ ВСеГО Произведено П Наблюдений ВеЛИЧИН XViyH (Xj, у,) —

результат г-го наблюдения (i= 1,2 п). Естественно принять, что

P0 + xip]+x]p2 + Po + xlP +хр2 + ...+хк2рк

Рк = У Уг

число п наблюдений не меньше, чем к + 1 — число неизвестных коэффициентов Pq,P, •••,/?„• Указанные коэффициенты должны являться приближенным решением системы линейных уравнений

-2■ +х?!рь = :

(5.9)

I Ро + хп Р + хп Рг + + хп Рк = Уп

х

4

х х2

4

Найдем Pq,P, .-tPh, применяя метод наименьших квадратов. Пусть

(5.10)

і

— матрица коэффициентов системы (5.9). Если столбцы матрицы А линейно независимы, то по теореме 1 предыдущего параграфа

т

(5.11)

получаем, что вектор-столбец р(pq,P, ..,Рк) коэффициентов «наилучшего» многочлена Р(х) является единственным решением системы

ATAp = ATY,

где Y=(y у2, ...,у„)Т— вектор-столбец, составленный из последовательных значений величины у.

Докажем, что в случае, когда все наблюдаемые значения величины х различны (XjXj при столбцы матрицы А линейно

независимы.

Предварительно докажем лемму. Ле мм а. При любом к > 1 справедливо равенство

Таким образом, в случае к 2 лемма доказана. Для определителя 0(3), проделав аналогичные преобразования, получим:

1

к к+1

П П (хгх). /=1 7=1+1

(5.12)

ДЗ) = (дг2 х,) (х3 х{) (х4 -*,)

х2 ^

(5.15)

Доказательство. Обозначим указанный определитель через Д/с). При k = 1 лемма очевидна:

Определитель, расположенный в правой части равенства (5.15),отли-чается от Д2) лишь заменой xi -> хм (;'= 1, 2, 3). Поэтому

Д1)

А А А

Для вычисления определителя Д2) =

1

х2

хъ

преобразуем его следующим образом:

вычитаем из третьего столбца второй столбец, умноженный на хх;

вычитаем из второго столбца первый столбец, умноженный нал,.

О

В результате получаем определитель

А-А

О

Д2) =

(5.13)

хз~х

Х2Х Х3Х

Разлагая определитель (5.13) по первой строке, получим

(5.14)

.2

..2

Д2) =

хз~х хї~хзх

Элементы первой строки определителя (5.14) имеют общий множитель (х2 *,); элементы второй строки имеют общий множитель (х3 *,). Вынесем общие множители. Получим

ХЪ х4

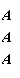
= (*3 хд (*4 х2) (*4 -^з)1

Следовательно,

ДЗ) = (х2 *,) (х3 jc,) (х4 *,) (хг х^ (х4 х2) (х4 х3).

Итак, лемма доказана и для к = 3. Отметим, что при доказательстве леммы для к 2 и к = 3 мы сводим вычисление определителя Д/t) к определителю вида ДА:-1). Аналогичным образом лемма доказывается и для к > 4.

(516)

Продолжим доказательство независимости столбцов матрицы А (см. (5.10)). Вычеркнем в этой матрице все строки с номерами больше к + 1, полученную матрицу обозначим А'. По лемме определитель матрицы А' равен произведению всех разностей вида x)-xi (j > і). Так как все х1 различны, то А * 0. Следовательно, столбцы матрицы А' линейно независимы; тем самым линейно независимы и более «длин-ные» столбцы матрицы А. Поэтому векторр = (Pq,P, —,Рі;) коэффициентов «наилучшего» многочлена Р(х) действительно является единственным решением (5.11) и может быть найден по формуле

{ATA)']ATY.

D(2) = (x2-xl)(x3-xl)

I

= (*2-*|Н*3-*і)С*3-*2)-

В качестве применения изложенных выше результатов найдем главную квадратичную тенденцию (тренд) изменения некоторой величины у по ее временному ряду У,У2>—>У„Для определенности

будем считать, что величина у измеряется ежемесячно в течение одного года (таким образом, л = 12). Мы хотим найти приближенную зависимость вида

y=pQ + pix+p2x2, (5.17)

где х — время. Пусть единицей измерения времени будет один месяц, положим,л:| = 1,дг2 = 2, ...,Х|2= 12. Тогда условие (5.17) приводит к

системе (5.9), в которой к = 2,п= 12. Соответственно система (5.7) § 5.1 приобретает вид

(АьА^)р0 + (А],А2)р1 + (А1,А3)р2 = (А], У),

1 (А2'АОРо + (АЬАі)Рі+(АьАі>Р2 = (АЬ У), (5.18) (A3,Ai)p0 + (A3,A2)pl+(A3,A£p2 = (A3, У),

где

Л,=(1, 1,..., 1)Г,

Л2 = („х2,...,12)г=(1,2,..., 12)r, Аъ = (х},х,...,х22)т=(1,,..., 144)Г,

Находим коэффициенты системы (5.18): {АХ,А)= 1 + 1 +...+ 1 = 12, (А],Аг) = {А2,А{) = 1 +2 + ... +12 = 78, (А,, Лз) = (А2> А$ = (А3, А,) = І2 + 22 + ... + 122 650, (А2> Aj) = (А3, Аі) = І3 + 23 + ... + 123 = 6084, (А3,А$= 14+24+...+ 124 = 60710. Таким образом, система (5.18) имеет вид

12р0 + 78р, +650/>2= У,,

• 78/>0 + 650/», + 6084р2 = У2, (5.19)

650/?0 + 6084/>, + 60710р2 = У3,

где

Y]=yi+y2 + y3+ ...+уі2 Y2 = yl + 2y2 + 3y3 + ...+ 12у12;

Y3=l2yl + 22y2 + 32y3 + ... + l22yl2.

12 78 650 78 650 6084 650 6084 60710)

Вычислив обратную матрицу для матрицы коэффициентов системы (5.19):

1,06818 -0,3409 0,02273 -0,3409 0,1336 -0,0097 0,02273 -0,0097 0,00075

находим искомые коэффициентыPq,p,p2pi = 1,06818У, — 0,3409У2 + 0,02273У3, р = -0,3409У, + 0,1336У2 0,0097У3, р = 0,02273-У, 0,0097У2 + 0,00075У3.

Пусть, например, у( — курс доллара США на последних торгах ММВБ /-го месяца 1992 г. (/ = 1,12). Тогда

У = (230, 139, 160, 144, 113, 147, 161,210,248,398,447,414). Вычисляя по приведенным выше формулам, находим:

У, =2812; У2 = 21924; У3 = 207664; ^ = 249; р = -51,91; /7 = 5,955.

Итак, мы установили, что квадратичная тенденция изменения курса доллара на торгах ММВБ в 1992 г. имеет вид

у = 5,955х251,91л: + 249. (5 2°)

Рассчитывая по формуле (5.20) «сглаженные» значения курса доллара, получим

.^ = 5,95551,91 +249 = 203;

>4 = 5,955-451,91 • 2 + 249 = 169и т. д.

Запишем эти 12 чисел в виде вектора

У = (203; 169; 147; 137; 138; 152; 178; 215; 264; 326; 399; 484).

Отметим, что У можно рассматривать как точку трехмерной плоскости Л, образованной всеми линейными комбинациями векторов AltA2,A3, ближайшую к точке У.

Соответственно Y* можно найти по формуле