§ 2.14. применение производных к исследованию функций
§ 2.14. применение производных к исследованию функций
Возрастание и убывание функции.Пусть X a R промежуток числовой прямой, т.е. Хэто либо отрезок, либо полуинтервал, либо интервал. Напомним, что функция/(х) называется возрастающей (убывающей) на промежутке X , если для любых х{, х2 є X, jc, < ху верно неравенство
f(xl)<f(x2)(f(x])>f(x2)).
Если в последнем неравенстве допускается равенство, то функция называется неубывающей (невозрастающей). Например, функция, принимающая постоянное значение_Д*) = const, является одновременно неубывающей и невозрастающей. По знаку производной («О», «+», «-») можно судить о характере изменения функции на промежутке (const, возрастает, убывает). В развернутом виде это утверждение дается ниже в теоремах 2.10, 2.11 и2.12.
Теорема 2.10. Пусть функция f(x) непрерывна на промежутке X, а ее производная f'{x) обращается тождественно в нуль внутри X. Тогда f(x) = const на X.
Доказательство. Пустьх, < х2 две точки на промежутке X. По теореме Лагранжа найдется точка с є(х,,х2), для которой
/ы-/(*)=
Так как х, < с < х2, то точка с является внутренней точкой промежутка X. Поэтому/'(с) = 0 и/(х2) = /(*,). Следовательно,/^) принимает постоянное значение на промежутке X.
С л едете ие I. Если эластичность функции у =/(х) тождественно равна нулю, то у = С const.
у'
Доказательство. Так как Еу = х— = 0 влечет у = 0, то по теореме 2.10 получаем, что у const. У
Следствие 2. Если эластичностьЕ^(*) = а не зависит от точки х, то у = Сх", где С const.
Доказательство. Так как эластичность функцииха
у
равна а, то эластичность функции z = — будет Е = а а = О
ха "
По следствию 1 имеем z = С const. Откуда у = Сха.
Теорема 2.11 (достаточное условие возрастания функции). Пусть функция f{x) непрерывна на промежутке X, а ее производная /'(х) неотрицательна внутри X и не обращается тождественно в нуль ни на каком интервале из промежутка X. Тогда fix) возрастает на X.
Доказательство. Пусть < х2 две точки из промежутка X. По теореме Лангранжа найдется точка с є (or,, х ), для которой
/ы-/(*.)=/'(*х*2-*,>
Так как х^ < с < х2, то точка с является внутренней точкой промежутка X. Поэтому Г (с) > 0 и f(x2) >/(*,). Таким образом, мы доказали, что функцияfix) не убывает на промежутке X. Следовательно, для любой точки х є (де,, дг2) выполняются неравенства /(*,)</(*) и/(*) </(х2). Предположим, что f(xl)=f(x2). Тогда для любой точки х є (jcp х2) имеем /(*,)=/(*) =/(*2), т.е. f(x) = const на интервале (дс,, х2). Но в этом случае /'(*) = 0 на (*i,x2), что противоречит условию теоремы. Поэтому/Ос,) < f(x2), a f{x) возрастает на X.
Следующая теорема доказывается аналогично.
Теорема 2.12 (достаточное условие убывания функции). Пусть функция f(x) непрерывна на промежутке X а ее производнаяfix) неположительная внутри X и не обращается тождественно в нуль ни на каком интервале из промежутка X. Тогда fix) убывает на X.
Пример 2.38. Найти интервалы монотонности функции у = х2 -6jc +10.
Решение. Имеем/ = 2*-6>0 при х > 3 и/ = 2к-6<0 при х < 3. Поэтому функция у = х26х + 10 убывает на интервале (оо, 3) и возрастает на интервале (3; + оо).
Пример 2.39. Найти интервалы монотонности функции
у = x-smx.
Решение . Находим производную у' = 1 cos х. Поскольку cos х < 1 при любом х, то у' > 0. Кроме того, производная у =i _cos х обращается в нуль только в изолированных точках х = Ink, где к целое число. Поэтому у' не обращается тождественно в нуль ни на каком интервале. Из достаточного условия возрастания функции следует, что функция у возрастает на R.
Экстремум функции. Точка х0 называется точкой локального максимума (минимума) функции f(x), если для всех х из некоторой окрестности точки х0 выполняется неравенство (рис. 2.10):
О
О
Xq~£ Xq Xq+£
/(*)</(*0) (/(*)*/М)
Xq-Є Xq Xq+£
Рис. 2.10
Очевидно, что у функции может быть несколько локальных максимумов и несколько локальных минимумов, причем некоторый локальный максимум может оказаться меньше какого-то локального минимума (рис. 2.11).
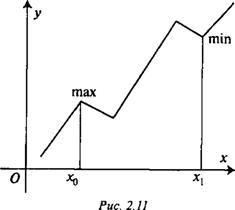
Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.
Теор ем а 2.13. Для того чтобы дифференцируемая функция f(x) имела в точке х0 локальный экстремум, необходимо чтобы в этой точке выполнялось равенство f'(x0) = 0.
Доказательство. Поскольку х0 точка экстремума, то существует такой интервал (х0 є, xQ + є), на котором f(xQ) -наибольшее или наименьшее значение. Тогда по теореме Ферма
Точки, в которых производная функции обращается в нуль, называются стационарными. Из теоремы 2.13 следует, что точка локального экстремума дифференцируемой функции является стационарной точкой. Обратное утверждение неверно. Рассмотрим, например, функцию/(х) хг. Эта функция возрастает на всей числовой прямой и поэтому не имеет точек локального экстремума. В то же время точка х = 0 является стационарной точкой, так как /'(*o) = 3V = 0.
Теорема 2.14. Пусть вторая производная дважды дифференцируемой функции f(x) принимает на промежутке X только положительные (отрицательные) значения. Тогда, если ха є х стационарная точка (функции f(x), то f(x0) наименьшее (наибольшее) значение функции f(x) на всем промежутке X.
Доказательство. Рассмотрим случай, когда вторая производная положительна. Тогда (f'(xQ))' > 0 и по достаточному условию возрастания функции получаем, что производная f'{x) возрастает на промежутке X.
Пусть х0 стационарная точка, f'(xQ) = 0. Тогда слева от х0 значения произвольной меньше нуля, а справа больше нуля. Следовательно, слева от х0 функция убывает, справа возрастает. Поэтому /jc0) наименьшее значение функции f{x) на промежутке X. Аналогично доказывается, что в случае /"(*) < 0 значение /(х0) является наибольшим.
Пример 2.40. Найти наибольшее значение/тах функции /(jc) = lnjc-ax
для произвольного положительного значения параметра а.
Решение. Производная /'(*) ~~~а обращается в нуль в точке хо=~Вторая производная f"{x) = aj = —у < 0. Поэтому значение в стационарной точке f(xQ) является наибольшим значением функции на интервале (0, +оо). Таким образом
Теорема 2.15. Для того, чтобы функция f(x) имела локальный максимум (минимум) в стационарной точке х0, достаточно, чтобы в окрестности этой точки существовала непрерывная вторая производная и выполнялось неравенство f"(xo)<0(f"(x0)>0).
Доказательство. Пусть f"(xQ) < 0. Так как /"(*) непрерывна в точке х0, то в некоторой гг-окрестности выполняется неравенство
f"(x)<0,x є(х0-є,х0 + є).
Следовательно, х0 точка локального максимума функции f(x). Аналогично доказывается, что в случае f"(x0) > 0 функция f(x) имеет локальный минимум в стационарной точке
Для того чтобы установить, что некоторая точка дг0 является точкой локального экстремума, в тех случаях, когда условия теоремы 2.15 не выполняются, можно попытаться воспользоваться следующим критерием (очевидно вытекающим из достаточного условия возрастания (убывания) функции).
Теорема 2.16. Если при переходе через точку х^ производная дифференцируемой функции f (х) меняет свои знак с плюса на минус, то точка х0 точка локального максимума функции f(x), а если с минуса на плюс, то х0 — точка локального минимума.
Прим ер 2.41. Найти точки локального экстремума функции у = Xі 2|х|.
Решение. Если х>0, то >> = х2 2х и У = 2х 2. Если х <О, то у = Xі + 2х и у'= 2х + 2. Решая уравнение у'= О, находим стационарные точки х12 = ±1. При х*0 вторая производная
 |
Наибольшее и наименьшее значения функции
на отрезке
Многие экономические задачи формулируются как задачи на нахождение максимального (минимального) значения функции на некотором множестве. Рассмотрим наиболее простой случай, когда требуется найти наибольшее (наименьшее) значение функции/(х) на отрезке [а, Ь]. В гл. 1 было доказано, что наибольшее (наименьшее) значение функции достигается в некоторой точке X, є [а, Ь]. При этом возможны лишь следующие три случая: 1) х0 = а, 2) х0 = Ь, 3) х0 є (а, Ь). Пусть х0 є (а, Ь). Тогда х точка локального экстремума и, если существует/'(х0), то/'(х0) = 0. Однако, производная f'(xQ) может и не существовать.
Определение. Критической точкой функцииf(x) называется точка, в которой производная f'(x) либо не существует, либо равна нулю.
Из определения вытекает, что точка локального экстремума х0 является критической точкой функции fix). Предположим, что критические точки функции Дх) на интервале (а; Ь) образуют конечное множество {х,, х2, хп}. Из сказанного выше следует, что точка х0, в которой функция принимает наибольшее (или наименьшее) значение, совпадает с одной из точек: а, Ь, х,, хя. Поэтому для максимального значения fmm функции Дх) на отрезке [а, Ь] имеем равенство
/_ = max{f(a),f(b),f(Xl),...,f{xn)}.
Аналогично для минимального значения /тп выполняется равенство
/тіп=тіп{/(4/(й),/(х1),..,/0п)}.
Пример 2.42. Найти наибольшее и наименьшее значение функции Дх) = х2ех на отрезке [3; -3].
Решение. Имеем /'(*) = 2хе* + х2е* = х(х + 2)е*. Критические точки: = 0, х2 = -2. Максимальное значение
/тах = тах{/(-3),/(3),/(0),/(-2)) = = тах{9е"3,9е3,0,4в"2} = 9е
Минимальное значение/тт= min{9e" 9е 0,4е"2} = 0.
Оценка числа корней уравнения. Рассмотрим уравнение
/(х) = 0,х є Л,
где/(х) многочлен третьей степени вида /(х) = хъ + рх + д. Если
коэффициентр > 0, то производная/'(*) = Зх2 + р > 0 и функция /(х) возрастает на R. Следовательно, многочлен /(х) имеет только один действительный корень. Если р < 0, то количество корней уравнения f(x) = О зависит от знака дискриминанта D, который определяется формулой*:
D = Ар1 -21q2.
Действительно, в случае р < 0 функция f(x) имеет две стационарные точки /, = и t2 = Эти точки разбивают R на
три промежутка таким образом, что f(x) возрастает на интервалах (м,/,),(*2,+°°) и убывает на (/,,/2). Находим значения многочлена в стационарных точках:
Откуда
Таким образом, если£> > 0, то числа/(/,) и /(/2) имеют противоположные знаки. Следовательно, на интервале (t,t2) много-член/(х) имеет один корень. Кроме того,/(дс) убывает на (/,, t2), поэтому/(/,) > 0, a f(t2) < 0. Так как lim f{x) = -со и/(/,) > 0,
то /О) имеет еще один корень на интервале (-«з,^). Так как Ніг^Ддг) = +оо и/(/2) < 0, то f{x) имеет третий корень на интервале (/2,+со).
Вывод: если дискриминант больше нуля, то многочлен имеет три действительных корня.
Аналогично доказывается, что в случае D < О многочлен имеет один действительный корень.
* Эквивалентов определение дискриминанта: D = (ab)2(b с)2(а с)2 , где а, Ь, сдействительные или комплексные корни многочлена/(х).
Покажем, как с помощью я-й производной /'"'(л:) можно получить оценку числа корней уравнения f(x) = 0.
Лемма. Если п раз дифференцируемая функция f(x) обращается в нуль в к точкаххх <х2 <...< хк на промежутке X,
то ее п-я производная f^{x) обращается в нуль на промежутке X по меньшей мере в (к и) точках.
Доказательство . Так как/(*,) =...= /(*„) 0. то по теореме Ролля найдутся точки /,,*2,...,/„_,, такие что /, е(х(,х1+1) и/'(/() = 0, (i = l,...,k1). Все точки /, еХ, поэтому первая производная /'(*) обращается в нуль на X по меньшей мере в к 1
точках. Так как/(/,)=...= /('*-,), то можно снова применить
теорему Ролля. В результате ее применения получим точки su...,sk_2, такие что-г, є(ґ,,ґ,+|) и/"(*,) = 0 (і = 1 А -2).
Точкил, принадлежат промежутку X, поэтому/"(■*) имеет наХпо меньшей мере к 2 точки, в которых она обращается в нуль. Повторяя описанную выше процедуру п раз, получим к п точек, в которых п-я производная обращается в нуль.
Теорема 2.17. Если уравнение/'"'(*) = 0 имеет г корней на промежутке X, то уравнение f(x) = 0 имеет на промежутке X не более п + г корней.
Доказательство. Пусть к число корней уравнения f(x) = 0 на X. По доказанной выше лемме имеем неравенство г>к-п. Откуда к < п + г.
Пример 2.43. Доказать, что для любого многочлена Р(х) степени п уравнение ех + Р(х} = 0 имеет не более п + 1 корней.
Решение. Найдем (« + 1)-ю производную функции /(*) = е1 + Р(х). Учитывая, что(ех)("+,) = ех,а (P(x)f"+]) = 0, получим /'л+1^х) = ех > 0. Следовательно, уравнение /^л+1'(д:) = О не имеет корней на промежутке (оо,+оо). Поэтому уравнение ех + Р{х) = 0 имеет не более и + 1 корней.
§ 2.15. Функция предложения конкурентной фирмы
Пусть некоторая фирма А предлагает свою продукцию к продаже по цене рА. Фирма А называется конкурентной, если существует такая цена р, что при цене рл < р фирма может продать
D(Pa) =
любое количество своей продукции, а при цене рА > р не может продать ничего. Таким образом, спрос на продукцию конкурентной фирмы имеет вид
+ оо, если рЛ < р, О, еслирА > р.
В данном случае кривая спроса является прямой, параллельной оси выпуска Oq(рис. 2.13), а сам спрос является совершенно эластичным. Для того чтобы какая-то реально существующая фирма могла считаться конкурентной, необходимо, чтобы максимальный объем ее выпуска составлял лишь незначительную долю от совокупного выпуска ее конкурентов.
Ра
Рис. 2.13
Для конкурентной фирмы невыгодно продавать продукцию по цене рА < р и невозможно продавать по цене рА > р. Поэтому мы
будем считать, что рА = р. Не имея возможности влиять на цену р, конкурентная фирма может увеличивать или уменьшать объем своего выпуска q так, чтобы получить максимальную прибыль x(q). Пусть C(q) издержки, связанные с производством q единиц продукции. Тогда
7c(q)=pq-C(q). (2.61)
Далее считаем, что функция C(qj определена и дифференцируема на промежутке [0,+оо). Таким образом, производная C'(q) определена при q > 0 и отождествляется, как обычно, с предельными издержками МС = C'(q).
Рассмотрим подробнее функции издержек следующих двух типов:
Тип I. Предельные издержки возрастают на промежутке [0,+«).
Тип II. Предельные издержки убывают на отрезке [0,<j0] и возрастают на интервале (q0 ,-н»).
В точке q* локального максимума функции прибыли л((]) выполняется равенство x'(q*) = рС'(я*) 0, из которого следует, что
Р = C'{q*)(2.62)
Для функции издержек первого типа верно следующее утверждение: если в точке q* предельные издержки совпадают с
иеной продукции (выполняется равенство (2.62)), тоя{с}*) -наибольшее значение прибыли на промежутке [0,+оо).
Действительно, функция C'(q) возрастает на промежутке [0,+оо). Следовательно, я'{^) = p-C'{(j) > 0, когда q < q* и я'(я) ~ Р ~ С'(я) < 0> когда q > q*. Поэтому прибыль x(q) возрастает на отрезке[0,д*] и убывает на промежутке[<7*,+°°) (см. теоремы 2.12, 2.11). Таким образом, q* точка глобального максимума функции прибыли.
Как и любая коммерческая фирма, конкурентная фирма стремится максимизировать свою прибыль, поэтому при данной цене продукциир она устанавливает объем выпуска q равным q*, где q* точка глобального максимума функции прибыли (2.61). Следовательно, равенство (2.62) влечет равенство q* = S(q), где S(p) функция предложения, т. е. S(p) обратная функция для функции Cq). С геометрической точки зрения данное утвержде
 |
ниє означает, что кривая предложения (график ) q = 5(р)сов-падает с кривой предельных издержек (графиком р = С'(ч)) (рис. 2.14).
Пр им ер 2.44. Найти функцию предложения конкурентной фирмы S(p), если ее функция издержек имеет вид
C(q) = q2 +64+5.
Решение. Находим предельные издержки C'(g) = 2q + 6.
Решая уравнение р = 2q + 6 относительно q, получим функцию предложения
Замечание. Если в примере 2.44 цена р = 10, то предложение 5(10) = 2 . Соответствующие издержки будут С(2) = 21, прибыль я-(2) = 10-2 — 21 = —1. Зачем же фирма решила выпускать 2 единицы продукции, если при этом она имеет убытки в размере 1 денежной единицы? Не лучше ли было прекратить выпуск? Ответ на эти вопросы состоит в том, что при выпуске q 2 фирма несет минимальные убытки. Если, например, она прекратит выпуск продукции (<7 = 0), то убытки составят я(0) = С(0) = 5 денежных единиц. Очевидно, что убыточное производство возможно только на коротком интервале времени, поэтому найденная функция предложения является функцией предложения в краткосрочном периоде.
Перейдем теперь к изучению функции предложения конкурентной фирмы в случае функции издержек второго типа. Пусть q -точка глобального максимума функции n(q) на промежутке [0,+со). Если q 0, то глобальный максимум будет также и локальным, Поэтому для точки q 0 выполняется равенство (2.62). Следовательно, q это либо 0, либо решение уравнения
P = C,{q (2.63)
 |
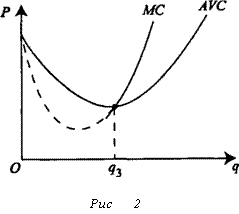 |
si ) =
Обсуждение Математика в экономике Часть 2
Комментарии, рецензии и отзывы
