Глава 1 введение в анализ §1.1. понятие функции. числовые функции и графики. обратная, сложная функции

Глава 1 введение в анализ §1.1. понятие функции. числовые функции и графики. обратная, сложная функции

Понятие функции одно из наиболее важных в математике и ее приложениях. В самом общем понимании функция это зависимость между двумя переменными. Уточнением этой идеи является следующее.

Определение. Пусть имеются два множества X и Y. Пусть, далее, указано правило, по которому каждому элементу х е X сопоставляется некоторый (единственный) элемент у є Y. Тогда говорят, что задано отображение или, по-другому, функция из X в У (рис. 1.1). При этом множество X называется областью определения функции.

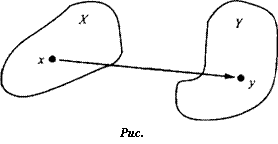Функции (как, впрочем, и другие объекты) в математике обозначают буквами. Чаще всего для этого используются буквы / g, h (латинского алфавита) или <р, у/(греческие). Обозначим данную нам функцию, например, буквой/ Обычно пишут так:

f.X^Y

что означает: / есть отображение множества X в множество Y. Для соответствующих элементов х и у используют запись

у=А*)

(«элемент у есть функция/ от элемента х»).

В курсе математического анализа изучают главным образом числовые функции. Числовая функция характеризуется тем, что оба множества Л"и Ксостоят из чисел, т.е. Ха R, У с Л. При этом переменный элемент х из X называется аргументом (или значением аргумента), а соответствующий элемент у функцией (значением функции).

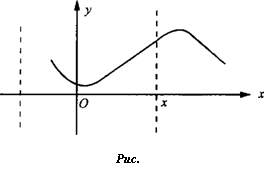
Наглядное представление о числовой функции дает ее график. Это некоторое множество точек на координатной плоскости, обычно некоторая линия.

Определение. Графиком функции f с областью определения X называется множество

Г= {(x,J[x))xeX).

Отличительной чертой каждого графика является то, что каждая прямая, параллельная оси ординат, т.е. каждая прямая х = const, пересекает его либо в единственной точке (если хеХ), либо вовсе не пересекает (если х € X); см. рис. 1.2.

В качестве примера приведем таблицу, содержащую данные о числе жителей, населяющих земной шар в отдельные годы:

Год	1800	1930	1960	1975	1987	2000
Млрд	1	2	3	4	5	б(прогноз)

Другие примеры: расписание движения поездов, таблица выигрышей в лотерее и т.п.

2. Аналитический, т.е. задание с помощью формулы, указывающей, какие действия нужно произвести над х, чтобы получить у. Например,

■у

у = -х + 1, у = [х] (целая часть х).

Замечание. Если функция задана формулой, а область ее определения не оговорена, то обычно подразумевается, что областью определения является множество всех значений х, для которых написанная формула имеет смысл (в школьной практике это множество называется ОДЗ областью допустимых значений для х). Например, в случае функции

областью определения является множество всех значений х, удовлетворяющих условию 1 -х2> 0, т.е. промежуток [-1; 1].

При аналитическом способе не исключается и такое положение, когда функция задается не одной формулой, а с помощью нескольких. Примером может служить функция

Остановимся кратко на способах задания функции.

В принципе задать функцию означает: указать множество X (область определения функции) и описать правило, позволяющее по данному значению хєХ аргумента находить соответствующее значение функции. Наиболее употребительными являются три способа задания функции:

1. Табличный. Используется тогда, когда область определения состоит из конечного множества чисел: Х= {*,, х2, хп}. Тогда для задания функции проще всего указать таблицу'

X	х	Х2		Хп
У	У	Уі		Уп

+1, если х > 0 0, если х = 0 1, если х < 0 .

обозначаемая sgn(x) (от лат. signum знак).

3. Графический, т.е. с помощью графика. На практике этот способ используется, например, в физических измерениях, когда зависимость у or х вычерчивается прибором (самописцем). Примером может служить снятие ЭКГ с больного.

Помимо «арифметических» действий над функциями, например, сложения, умножения и т.д., существуют еще несколько операций, позволяющих по данным функциям строить новые функции. Наиболее важными из них являются две операции:

Построение обратной функции. Пусть у =J{x) функция с областью определения X. Обозначим множество всех значений функции (т.е. множество всех чисел J(x), где х є X) через У. Пишут обычно: D(J) = X, E(J) = У. Предположим дополнительно, что разным значениям х отвечают разные значения у:

Х]*х2 => ух * у2

(ясно, что не всякая функция удовлетворяет такому условию: примером может служить функция у = х2,х є R). Тогда для каждого значения^ є У существует только одно х є X, такое, чгоДх) = у. Если мы сопоставим каждому у є Y именно такое х, то получим отображение множества Y в множество X. Это отображение называется обратным к данному отображению / и обозначается /~ Таким образом:

f-.X^Y, Ґ:У^Х,

причем связь между / и устанавливается соглашением: если

то Г1 (>>)=*• . Итак, обратная функция для у =J{x) есть х

= Г (У)Обычно

аргумент в обратной функции обозначают буквой х, а значение функции буквой у. Тогда обратная функция запишется >> = /"'(*)■

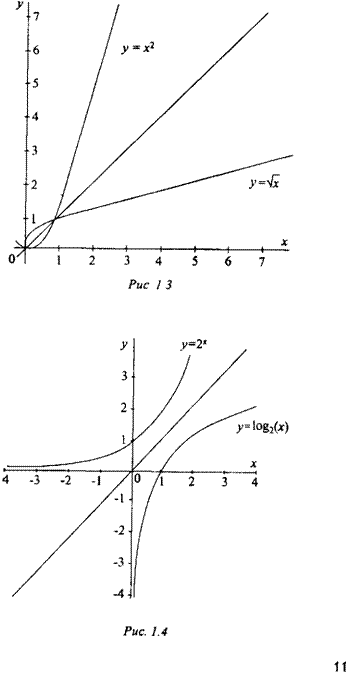
Пример. Пусть у Xі. Если за область определения Щу) принять множество всех действительных чисел, то Е{у) = [0; оо), и обратной функции не существует, так как х = ±Jy (два значения, а не одно). Если же принять ЕНу) = [0; оо), то будем иметь обратную функцию д: = Jy , определенную на множестве [0; да) и принимающую значения в том же множестве. Меняя обозначения, получим запись обратной функции в виде y = Jx. На рис. 1.3 приведены графики исходной функции = х2, Х= [0; оо), и обратной функции (с измененными обозначениями) у = 4х , Х= [0; да). Эти графики симметричны друг другу относительно «биссектрисы» 1-й и Ш-й координатных четвертей.

Вообще, графики исходной функции у = J[x) и обратной у =/"'(*) всегда симметричны друг другу относительно указанной биссектрисы (почему?).

Для иллюстрации приведем еще один пример (рис. 1.4): график функции_у = 2ЕКх) = (-со; оо), Е(у) = (0; оо)) и обратной функции у = log2 x(D{x) = (0; оо), Е(у) = Но, оо).

Построение сложной функции. Пусть даны две функции: х = h(t) с областью определения Т и множеством значений X, и у = g(x) с областью определения X и множеством значений У

Тогда «цепное» правило:

/—*-»х—

определяет новую функцию с областью определения Т. Эта новая функция обозначается

у = g(K'))

и называется сложной функцией, или функцией от функции.

Например, две функции у = lgx и х = t + 2 определяют сложную функцию у = lg(t +2) с областью определения t + 2 > 0.

Элементарные функции

Наиболее простые приложения математического анализа ограничиваются кругом так называемых элементарных функций. Перечислим сначала основные элементарные функции. Это:

Степенные функции, у = ха,

где а любое постоянное число. Областью определения считается промежуток х > 0, хотя в некоторых случаях, например, если а натуральное число, функция определена для всех х.

Показательные функции: у = 0х,

где а > 0, а * 1. Область определения множество всех действительных чисел.

Логарифмические функции: у = log^x, где а > 0, а * 1. Область определения: х > 0.

4. Тригонометрические функции: у = sin х, у = cos х, у = tg х.

Область определения для sin х и cos х множество действительных чисел.

5. Обратные тригонометрические функции: у = arcsin х,

у = arccos х, у = arctg х.

Область определения: х е [-1; 1] для arcsin х и arccos х, множество действительных чисел для arctg х.

Укажем теперь действия над функциями, которые мы будем называть допустимыми. Это:

все арифметические действия (/ + g,f g,f g, —);

построение сложной функции. s

Определение. Элементарными функциями называются такие, которые получаются из основных с помощью допустимых действий.

Например, у = Vl -Xі = (1 X1)2,у = 1 + Vlgsin2яг ит.п. Во всех указанных примерах областью определения функции можно считать ОДЗ (или часть ОДЗ).