§ 4.6. приложения определенного интеграла

§ 4.6. приложения определенного интеграла

1. Вычисление площадей плоских фигур

В предыдущем параграфе мы рассмотрели понятие определенного интеграла и выяснили, что для непрерывной неотрицательной функции у= f(x), заданной на отрезке [а, Ь], определенный интеграл от данной функции по данному отрезку дает площадь криволинейной трапеции аЛВЪ (рис. 4.10).

Пример 4.31. Найти площадь криволинейной трапеции ограниченной графиком функции = sin2* на отрезке [0, *] Искомую площадь S находим по формуле 2

Интересно, что мы могли прийти к тому же результату без использования интеграла. Действительно, легко видеть, что S равна площади, ограниченной на том же отрезке функцией у cos2*, поскольку по формуле приведения графики этих функций получаются друг из друга сдвигом вдоль оси Ох. Однако sin2jc + cos2* = 1, поэтому S + S = л/2, откуда получим искомую формулу.

С помощью интеграла можно находить площади плоских фигур более сложного вида, нежели криволинейная трапеция.

Рассмотрим фигуру, ограниченную слева прямой х = а, справа прямой х = Ъ (а<Ь), снизу графиком неотрицательной функции у =/(*) и сверху графиком функции у = /2(х) (f^x) ^/2(х)) (рис. 4.11, на котором фигура А]А2В2В] выделена штриховкой).

' = Jsin2 xdx.

Чтобы вычислить этот интеграл, воспользуемся тригонометрической формулой понижения степени sin2 ^-bfS!2^ Тогда

получим

2 L л _ я ~ 2'Г~4'

2

sin 2*

cos2jtt&

1-cos 2л: 1 2 ~2І

Таким образом, искомая площадь s = —

4"

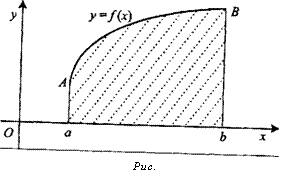
Площадь фигуры А1А2В2В1 можно вычислить следующим образом

* ь

S = SaA2B2b ~ SaAxByb = fl-fy = a a

ь (4.16) = J(/2 (*)-/,(*))&.

Условие неотрицательности функции fs(x) vif2(x) можно снять. Действительно, пусть т наименьшее значение функции/,(*) на отрезке [а, Ь]. Тогда функции А,(х) = /, (х)+т и h(x) = /2(х)+т

17*

259

непрерывны и неотрицательны на отрезке [а, Ь], и мы можем применить формулу (4.16):

а а а

Таким образом, формула (4.16) выполняется и в этом случае. Графическая иллюстрация приведена на рис. 4.12.

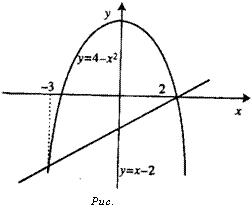
Для этого, в частности, необходимо найти точки пересечения двух данных линий. Имеем х 2 = 4 х2, откуда х2 + х 6 = 0, так что х, = -3, х2 = 2. Поэтому пределы интегрирования будут а = -3, Ь = 2. Таким образом,

* 1 2 3

5= J(4-x2-(x-2))<k = |(б-х-х2)дх = 6х--— —

-3

8 ( 9 і 1 1 5

= 12-2 18 — + 9 =7+13= 20-.

3 V 2 ) 3 2 6

2. Вычисление объема тела вращения

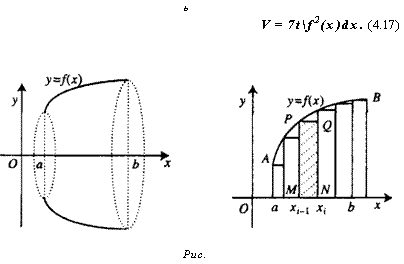
Оказывается, что с помощью определенного интеграла можно вычислять не только площади, но и объемы фигур. Пусть функция^ =f(x) непрерывна и неотрицательна на отрезке [а, Ь]. Тогда тело, которое образуется при вращении вокруг оси Ох криволинейной трапеции аАВЬ (рис. 4.14), имеет объем

Пр и мер 4.32. Найти площадь фигуры, ограниченной прямой^ = х 2 и параболой^ = 4-х2.

(рисПГіЗ)Є ВСЄГ0 ПОСтроим Ф"^* площадь которой мы ищем

Чтобы доказать формулу (4.17), выполним разбиение Т отрезка [а, Ь] точками а = xQ < х. < х2 <...< х^, < хя = Ь. На каждом отрезке разбиения [jcj(, xj построим прямоугольник MNQP (рис. 4.14), высота которого MP = mi равна наименьшему значению функции .у =/(х) на указанном отрезке. При вращении вокруг оси Ох прямоугольник MNQP опишет цилиндр, объем которого будет равен v( = лт12Ах1, где Дх, = х, х, ,.

Сумма объемов всех таких цилиндров для данного разбиения запишется в виде следующей суммы

vT = x^m2Ax,.

Если бы мы вместо наименьшего значения функции f(x) брали бы наибольшее значение, то получили бы сумму

УТ = я^М2Ах,.

i=i

С одной стороны ясно, что при измельчении разбиения Т обе эти суммы дают приближенное значение искомого объема V, а с другой стороны, эти суммы являются нижней и верхней суммой Дарбу для функции у =я/2(х). Последняя функция непрерывна, поскольку непрерывна функция у =f(x) и, следовательно, интегрируема, откуда и следует формула (4.17).

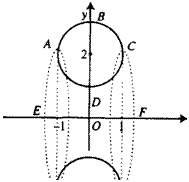
Пример 4.33. Окружность единичного радиуса с центром в точке 0(0, 2) вращается вокруг оси Ох (рис. 4.15). Найти объем тела вращения. (Это тело называется тором.)

Уравнение окружности имеет вид: х2 + (у If = 1. Выражая у через х, получим уравнение ABC:

у=/,(х)=2+>/Г^7

и уравнение ADC:

у = /2(х) = 2-у[ї^хТ.

Объем тора можно представить в виде разности объемов тел, полученных от вращения криволинейных трапеций EABCF и EADCF. Используя формулу (4.17), получим

V = я )f2{x)dx -я f2(x)dx = я f(/,2(x) f2{x))dx =

-I -1 -1

1 I

= я J4 ■ l4-x2dx = 8* j7l^ Xі dx. -і -і Похожий интеграл мы уже рассматривали в качестве примера 4.29 предыдущего параграфа и выяснили, что он дает площадь полукруга единичного радиуса, т.е. я/2. Подставляя это выражение в последний интеграл, окончательно получим

F = 4^2.

Рис. 4.15

3. Экономические приложения определенного интеграла

В курсе микроэкономики часто рассматривают так называемые предельные величины, т.е. для данной величины, представляемой некоторой функцией _у =Дх), рассматривают ее производную /'(*)• Например, если дана функция издержек С в зависимости от объема q выпускаемого товара С = C(q), то предельные издержки будут задаваться производной этой функции МС = С '(q). Ее экономический смысл это издержки на производство дополнительной единицы выпускаемого товара. Поэтому часто приходится находить функцию издержек по данной функции предельных издержек.

Пример 4.34. Дана функция предельных издержек МС = 3q2 48^ + 202, 1 < q < 20. Найти функцию издержек С = C(q) и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 50 руб.

Функцию издержек находим интегрированием:

ч

C(q)= $MCdq + C0,

і

где константа С0 находится из данного условия С(1) = 50, так что С0 = 50, поскольку интеграл обращается в нуль. Интегрируя, получим функцию издержек

C(q) = q3 -24q2 +202q + 50.

Подставляя q = 10 в полученную формулу, находим искомое значение

С(10) = 670.

Еще одним примером приложения определенного интеграла является нахождение дисконтированной стоимости денежного потока.

Допустим вначале, что для каждого дискретного момента времени t = 1,2, 3, ... задана величина денежного потока /?(/). Если ставку процента обозначить через р, то дисконтированную стоимость каждой из величин R(l), R(2), R(3),... мы найдем по известным формулам

R(l)(l + pyR(2)(l + PyR(3)(l + P)-....

Тогда дисконтированную стоимость денежного потока мы найдем, суммируя эти величины

П = 1>('Х1 + />Г'' (4.18)

где п общее число периодов времени.

В непрерывной модели время изменяется непрерывно, т.е. для каждого момента времени 0 < / < Т, где [0, 7] рассматриваемый период времени, заданная величина /(/) скорость изменения денежного потока (т.е. величина денежного потока за промежуток времени от / до / + dt приближенно равна I{i)dt). Для нахождения величины П изменим формулу (4.18). А именно, знак суммирования заменим на знак определенного интеграла, формулы нахождения дисконтированной стоимости в дискретном случае заменим

(4.19)

на их непрерывный аналог, и тогда формула (4.18) примет следующий вид:

П= l(t)e-p,dt.

Пример 4.35. Под строительство гидроэлектростанции задан непрерывный денежный поток со скоростью /(/)= -t2 + 20/ + 5 (млрд руб./год) в течение 20 лет с годовой процентной ставкой р = 5\%. Найти дисконтированную стоимость этого потока.

По формуле (4.19) имеем

20

П = J(-/2 +20t + 5)e-00i'dt.

о

Чтобы вычислить этот интеграл, выполним сначала замену переменной

s = -0,05/, / = -20s, dt = -20ds.

При этом новые пределы интегрирования получаются подстановкой старых пределов в формулу замены: s0 = 0, s, = -1. Получим

-1 о

П -20 J(400/ 400s + 5)e'ds = 20 J(400s2 400s + 5)e'ds.

о -і

К последнему интегралу применим формулу интегрирования по частям, полагая и = -400s2 400s + 5, du = (-800s 400)ds, dv esds, v = e$. Поэтому

о о.

П = 20

iL. 400s2 400s + 5y + Je* (800s + 400)ds

< -i-i

В первом слагаемом подставим пределы интегрирования, а к второму слагаемому еще раз применим формулу интегрирования по частям, полагая и = 800s + 400, du = 800<is.

( , v Ї

П = 20 55<?"' + (800s + 400)еТ, Ше'сЬ =

-і /

= 20(5 5е"' + 400 + (800 400)<Г' 800 + 800е"') = = 20(1195е-' -395). Окончательно получим: П = 892 (млрд руб.).

Далее мы рассмотрим некоторую модель экономического роста, предложенную Е. Д. Домаром. Основные допущения этой модели сформулированы ниже.

Всякое изменение величины скорости денежного потока /(/) влияет как на совокупный спрос, так и на изменение объема производства.

Скорость изменения величины спроса Y(t) пропорциональна производной скорости денежного потока с коэффициентом пропорциональности к = 1/5, где s предельная величина накопления. Это предположение можно записать в виде уравнения:

dY 1 dl

— = -—■ (4.20)

dt s dt v '

Экономический потенциал к (т.е. величина стоимости товаров, которые можно произвести) пропорционален объему оборотных средств А" с коэффициентом пропорциональности р, т.е. к = рК. Дифференцируя по /, получим

dn dK ,

~ = Р^-РІ. (4.21)

В модели Домара предполагается, что весь экономический потенциал полностью используется, иными словами, Y= к. Дифференцируя по /, получим

^ = ^. (4.22) dt dt '

Подставляя (4.20) и (4.21) в (4.22), имеем

(4.23)

1 dl т dl

—— = pi или — = psdt.

s dt I

Чтобы найти функцию /(/) из уравнения (4.23), проинтегрируем обе части последнего равенства по t от 0 до t Получим

/у= fxdt,

= pst

или

1п|/(0

откуда

1п|/| = 1п|/(0)| + /ю/.

Потенцируя последнее равенство, получим окончательное выражение для /(/):

I(t) = I(Q)e<", (4.24)

где /(0) это скорость денежного потока в начальный момент времени.

Таким образом, для того, чтобы поддерживать равновесие между объемом производимых благ и совокупным спросом на них, скорость денежного потока должна расти с экспоненциальной скоростью, согласно формуле (4.24).

Модель Домара это типичный пример модели роста, записываемой в виде одного или нескольких уравнений, в которые входят производные неизвестных величин. Такие уравнения называются дифференциальными, они будут рассмотрены ниже в этой книге. Существенным компонентом решения таких уравнений является применение интегрирования.