§ 4.7. несобственные интегралы
§ 4.7. несобственные интегралы
Вводя понятие определенного интеграла, мы предполагали, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. В противном случае множество сумм Дарбу не будет ограниченным. Однако возможны случаи, когда одно или оба этих условия не выполняются. В таком случае соответствующие интегралы называются несобственными. Мы будем различать два случая: промежуток интегрирования бесконечен или подынтегральная функция не ограничена.
1. Несобственные интегралы с бесконечными
пределами интегрирования
Начнем со случая, когда промежутком интегрирования является луч [а, +оо).
Определение.Пусть функцияу= f(x) интегрируема на каждом конечном отрезке [ a, b] (Ь > а), т.е. существует опреь
деленный интеграл 1(b) = jf(x)dx. Тогда за несобственный ина
теграл jf(x)dx принимают предел функции 1(b), когда Ь стремится к бесконечности
+00 Ь
f{x)dx=vm [f{x)dx. (4.25)
a a Ь
Если предел lim f/(x)dx существует и конечен, то говорят,
что несобственный интеграл сходится.
Если предел в правой части (4.25) не существует, то несобственный интеграл расходится.
По аналогии с определением (4.25) можно рассмотреть несобственный интеграл с бесконечным нижним пределом, а именно,
4 4
jf(x)dx = Шп jf(x)dx. (4.26)
-оо а
Наконец, можно рассмотреть несобственный интеграл с бес-конечными нижним и верхним пределами J/(x)dx. Для этого
-оо
возьмем произвольную точку с. Она разобьет числовую ось на два луча (-оо, с] и (с, +оо]. Если существуют несобственные интегралы jf(x)dx и ^f(x)dx, то говорят, что существует и не-00 <~
00
собственный интеграл ^f(x)dx. В этом случае полагают
-ОО .
00 с +оо
jf(x)dx = f(x)dx + f{x)dx. (4.27)
-00 00 С
Нетрудно показать, что правая часть формулы (4.27) не зависит от выбора промежуточной точки с.
Геометрический смысл несобственного интеграла
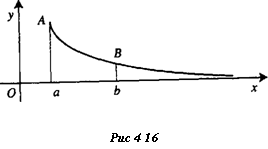
Пусть дана неотрицательная функция у = fix), непрерывная на луче [а, +оо). Для каждого Ъ > а определенный интеграл jf(x)dx дает площадь криволинейной трапеции аАВЬ. 268
Мысленно перемещая отрезок ВЬ направо, мы получим в качестве значения несобственного интеграла jf(x)dx площадь «греа
ах_
2 "
 |
Пример 4.36. Найти несобственный интеграл jі х
По определению имеем
Й-= lim x-2dx = \m-- =limf-+ ll = l. Таким образом, несобственный интеграл сходится и равен 1.
"cdx
Пример 4.37. Найти несобственный интеграл J~J^' Имеем
f-=L= lim [x~2dx=lim2jx~ = Iim(2v£-2) = со.
1 vx , ,
В данном случае несобственный интеграл расходится (предел равен бесконечности).
Пример 4.38. Найти несобственный интеграл jcos2xdx.
_ п В данном случае
 |cos2;u£t = lim co?,2xdx lim
|cos2;u£t = lim co?,2xdx lim
sin2jc
sin 26
ь->оо 2
и интеграл расходится, поскольку данный предел не существует.
О
а
Ь х
Рис. 4.17
(4.28)
Пример 4.39. Рассмотрим ситуацию, когда денежный поток не прекращается никогда, например, в случае эксплуатации земельного участка. Если г непрерывная процентная ставка, а R(t) соответствующая рента, то нахождение дисконтированной стоимости земельного участка приводит к формуле, включающей несобственный интеграл
П = JR(t)e"dt.
6,25 (млн руб.).
П= se-°
Пусть R(t) = 5е~°-7' (млн руб./год) рента, получаемая от земельного участка, г= 10\% процентная ставка. Определим его дисконтированную стоимость по формуле (4.28):
.-0.8'
■0,8
0,8
7'-Є-0'"Л=5|в-°-,,Л:
о
Интересно сравнить эту величину со стоимостью участка в данный момент времени, которая равна /?(0) = 5 (млн руб.).
Определение. Пусть функция у = fix) »« ограничена на отрезке [а, Ъ], однако интегрируема на любом меньшем отрезке [а Ь-є], гдеє>0. Тогда, если существует конечный
Ь-е
предел J^0 j/(*)<fr> то его принимают за несобственный интеграл jf(x)dx от неограниченной функции fix).
а
Таким образом,
* Ь-є
J/M*=Ao I'M*<4-29>
а а
В этом случае говорят, что несобственный интеграл (4.29) сходится. Если предел не существует или бесконечен, то (4.29) расходится.
Аналогично, если х = а особая точка, то несобственный интеграл определяют так:
ь ь
1#8А )>(*)*• (4-3°)
2. Несобственные интегралы от неограниченных функций
Пусть функция у -fix) определена на промежутке [а, Ь). Точку х = Ъ будем называть особой, если функция Дд:) не ограничена в любой окрестности этой точки, но ограничена на любом отрезке, заключенном в промежутке [а, Ь) (рис. 4.17).
Если же х — с единственная внутренняя особая точка на отрезке [а, Ь], то полагают
Ь с Ь
f(x)dx = f(x)dx + f{x)dx, (4.31)
а а с
при условии, что оба несобственных интеграла справа сходятся.
Если особых точек на отрезке [а, Ь] несколько, то отрезок разбивают таким образом, чтобы в каждом отрезке разбиение было не более одной особой точки, и используется определение (4.31).
Пусть F(x) первообразная для функции j(x). Положим F(a + 0) = Xvm^ F(a + є), F(b 0) = ^limo F(b e) (если эти пределы существуют). Тогда аналогом формулы Ньютона-Лейбница для сходящихся интегралов, у которых особыми точками являются только х = а и х = Ь, будет следующая формула:
ь
Jf(x)dx = Fib 0) F{a + 0). (4.32)
a
В случае непрерывной функции Fix) получим формулу, по форме полностью совпадающую с формулой Ньютона-Лейбница:
ь
f(x)dx = Fib)-F(a). (4.33)
'rdx
Пример 4.40. Найти интеграл |~7=
Подынтегральная функция /(*) = имеет единственную особую точку х = 0 на отрезке интегрирования [0, 1]. Первообразной
для этой функции будет F(x) = 2-Ух, которая непрерывна на этом отрезке. По формуле (4.33) имеем:
Подынтегральная функция /(*) = — имеет на промежутке интегрирования [0, 1] единственную особую точку х = 0. Первообразной для нее будет F(x) = lnx. Поэтому имеем
rdx cdx І,
— = lim —= lim lnx ' = lim (lnl-ln£y=lim ln£' = +oo.
J X £-*0+q J X £->0+0 1 c-»0+0 £-»0+0 0 с
Таким образом, данный несобственный интеграл расходится к +оо.
Имеется тесная связь между несобственными интегралами с бесконечными пределами и интегралами от неограниченных функций. Покажем это на предыдущем примере. Выполним замену переменной
1 1 , dt
/ = —, х = -, dx = —-. х / t2
Верхний предел интегрирования не изменится, а нижний предел интегрирования будет равен +оо, поскольку Hm — = +а>. Таким образом,
11 +о0 +со
J x " J t2 " J7" JT"
Поэтому последний несобственный интеграл с бесконечным верхним пределом также расходится.
і
= 2-0 = 2.
о
Таким образом, данный несобственный интеграл сходится и равєн 2.. * § 4.8. Приближенное вычисление определенных интегралов
В том случае, когда первообразная подынтегральной функции известна, например, является элементарной функцией, определенный интеграл вычисляют по формуле Ньютона-Лейбница. Однако часто возникает ситуация, когда первообразная либо не выражается в виде элементарной функции, либо выражение для первообразной выглядит слишком сложно. В этом случае применяют приближенные формулы вычисления определенных интегралов.
Мы познакомимся с двумя из них формулой прямоугольников и формулой трапеций.
Основная идея получения этих формул состоит в замене подынтегральной функции на функцию более простого вида, например, многочлен, интеграл от которого находят непосредственно по формуле Ньютона-Лейбница.
Jf(x)dx * /(*,) ■ 2h + f(x,) ■ 2h+.. .+/(дг2и_,) 2h =
a
= 2h(f(xx) + f(xi)+...+f(x2n_l)).
(4.34)
1. Формула прямоугольников
Здесь h длина отрезка разбиения, A = ^^> абсциссы x2k_v 1 < к < n вычисляют последовательно:
и
Пусть требуется вычислить определенный интеграл J/(x)dx,
а
< X
<X
<*2п=Ь.
<X2k <...<X
2k-2
2k2n-2
2n-l
где fx) интегрируемая функция на отрезке [а, Ь]. Разобьем отрезок интегрирования на 2л равных частей:
а = хп < х, <х-> <...< х
На каждом отрезке [х2*-2> *2jJ' как на основании cd, построим прямоугольник высоты Ax2ki) cCDd (рис. 4.18). Площадь криволинейной трапеции аАВЬ заменим на сумму площадей всех таких прямоугольников. Таким образом, определенный интеграл приближенно равен следующей сумме:
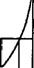
а хх хг
Хіл-2 Ъ X х2я-1
х2к-2 х2к х1кРис. 4.18
В

О
xx=a + h, x2k+x=x2k_x+2h, к = 1,2,...,я-1.
Формулу (4.34) называют формулой прямоугольников.
Пример 4.42. Вычислить с точностью до ІО-3 определенный интеграл je~*2dx, используя формулу прямоугольников.
-і
Полагаем f(x) = е-*2, а = -1, Ь = 1, T0I*a h = -■ Расчетные формулы выглядят следующим образом:
х, = а + A; s0 = 0; 1 < і < п, = х, + 2А; s, = + /(*,); Sn = 2hs„. Результаты вычислений приведены в следующей таблице.
| и | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
| S п | 2 | 1,558 | 1,509 | 1,497 | 1,495 | 1,494 | 1,494 |
Как видно из таблицы, точное значение интеграла с заданной точностью получается уже на шестом шаге.
Доказано, что погрешность применения формулы (4.34) не больше чем
(Ь-аУ „
где М максимум значений второй производной на данном отрезке. Обычно вычисления заканчивают, когда модуль разности S2-Sn становится меньше заданной точности.
 |
Для получения приближенной формулы вычисления определенного интеграла более высокой точности, нежели формула прямоугольников, будем вписывать вместо прямолинейных отрезков куски парабол.
Лемма 1. Через любые точки A/,(jc,, yt), М2(х2, у2), A/3(jc3, уъ), с различными абсциссами можно провести единственную
параболу:
у = ах2 +Ьх + с.
(4.35)
Доказательство. Дня нахождения неизвестных коэффициентов а, Ъ, с подставим в уравнение (4.35) координаты данных точек MvM2,My Получим систему уравнений:
Доказательство. В этом случае система (4.35) приоб-ретает вид
ах1 + bx,+c = yl ах + Ьхг + с = уг ах] + Ьх3+с = у}
ХІ X, 1
Д =
Определитель этой системы
= (*2-*.X*3-*zX*3-*.)
1
не равен нулю, поскольку все числа х{,х2, х3 по условию различны. Поэтому эта система имеет единственное решение, что и требовалось доказать.
(4.36)
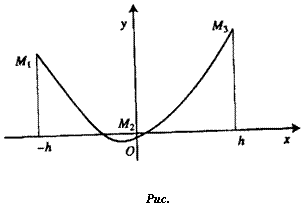
Лемма 2. Площадь s криволинейной трапеции, ограниченной параболой у = ах2 + Ьх + с, проходящей через точки М,(-А, у{), М2(0,у2), М3(Л,^3), (рис. 4.19), выражается формулой
^-{Уі+4уг+у3).
ah1 -bh + c = y{ ah1 + bh + c = y3
откуда lah2 + 2c = yt+ yy Поэтому
s= j(ax2 +bx + c)dx = ${ахг +c)dx+b xdx = 2){ax1 +c)dx =
-h -h -A 0
= 2^ay + erj = |(2oAJ +6c) = ^(y, +4y2 +y3).
Рассмотрим криволинейную трапецию, ограниченную графиком функции у -J(x) и разобьем отрезок интегрирования [а, Ь] на 2п равных частей точками
а = х0 <х, <хг <...<хи <xIt+l <хг„„г <..<хи.г <*,„., <хи =6. Через каждые три точки
МаМу Л/2,..., Ми Ми^ MUtlми.1м1я.іми
проведем параболу (лемма 1). В результате получим и криволинейных трапеций, ограниченных сверху параболами. По лемме 2 площадь каждой такой частичной криволинейной трапеции, опирающейся на отрезок [х2к, JCj^j], равна:
f b-a
J f(x)dx~*-j—(y2k + 4y2k+i +y2k+2),
*2k
гдеук =Axk), 0 < к < In. Складывая почленно эти приближенные равенства, получим приближенную формулу
4 л-1
J/(X)<& й -^-^(Угк +*У2п-2 +У2к+2) а к=0
или в развернутом виде
* Ъ-а
f(x)dx»^(y0+y2n+2(y2+..^y2n,x) + A(y^..^y2n_^. (4.37)
а
Формула (4.37) называется формулой Симпсона. В формуле Сим-псона значения функции J[x) в нечетных точках разбиения Хр х2п_х имеют коэффициент 4, в четных точках х2, х2п_2 коэффициент 2, в граничных точках коэффициент 1.
Можно показать, что погрешность формулы (4.37) не больше
чем
(Ъ-а)' М 2880л4 '
где Мнаибольшее значение модуля четвертой производной данной функции на отрезке [а, Ь].
Пример 4.43. Вычислить приближенно определенный интеграл из примера 4.42, используя формулу Симпсона.
Чтобы сравнить результаты вычислений по формулам прямоугольников и Симпсона, будем брать одинаковые разбиения отрезка [-1,1], причем число п подбирать таким образом, чтобы наиболее трудоемкая часть вычислений нахождение значений функции была одинаковой. Результаты вычислений приведены в следующей таблице.
Сравним эффективность вычислений для этих двух методов. Мы видим, что формула Симпсона дает три верных знака после запятой при разбиении отрезка на 4 интервала. При использовании формулы прямоугольников понадобилось 64. Мы получим 5 верных знаков после запятой при 2и = 16!
Таким образом, формула Симпсона дает значительный выигрыш в точности при незначительном усложнении вычислительной схемы и примерно том же объеме вычислений.
В заключение отметим, что в некоторых случаях (очень дорогие или труднодоступные значения функции) применяют другие вычислительные схемы Гаусса и Чебышева, которые за счет тщательного выбора значений функции позволяют находить приближенно значения определенных интегралов еще более экономным способом.
| 2п | 4 | 8 | 16 | 32 |
| s2n | 1,49436 | 1,49371 | 1,49365 | 1,49365 |
Обсуждение Математика в экономике Часть 2
Комментарии, рецензии и отзывы
