§ 5.2. ряды с положительными членами.

§ 5.2. ряды с положительными членами.

Признаки сходимости

В данном параграфе рассматриваются ряды а, + а2 +... + а+..., все члены которых положительны. Вопрос о сходимости таких рядов решается особенно просто.

1. Критерий сходимости

Теорема 5.2. Для того, чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Доказательство .Необходимость. Пусть ряд а, + а2 + ... + ая+... сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует, что последовательность частичных сумм ограничена.

Достаточность. Поскольку все члены данного ряда положительны и для любого п S^S^ + a^ то последовательность его частичных сумм монотонно возрастает. Однако известно, что ограниченная сверху монотонная последовательность имеет предел.

Указанный критерий имеет скорее теоретическое, нежели практическое значение. Однако он является основой, на которой базируются другие признаки сходимости. Все они являются только достаточными.

2. Достаточные признаки сходимости

Теорема 5.3 (первый признак сравнения). Пусть даны два ряда с положительными членами:

al + a3+... + a+...t (5.10)

b] + b2+... + b+... , (5.11)

причем члены первого ряда не превосходят соответствующих членов второго: ап<Ъ (п = 1, 2, ...). Тогда из сходимости второго ряда («большего^ следует сходимость первого ряда («меньшего»). Эквивалентно, из расходимости меньшего ряда следует расходимость большего ряда.

Доказательство. Обозначим соответственно Sn и Тл частичные суммы меньшего и большего рядов (5.10) и (5.11). Тогда для всех п выполняются неравенства

S<T. (5.12)

ЯП v '

Поскольку больший ряд сходится, то по критерию сходимости последовательность его частичных сумм {Г } ограничена, т.е. существует такое число С, что для всех п выполняются неравенства Т <С. Тогда из (5.12) следует, что такие же неравенства выполняются и для частичных сумм Sn, т.е. последовательность {SJ также является ограниченной. По теореме 5.2 меньший ряд сходится, что и требовалось доказать.

(5.13)

(п + )2

Пример 5.7. Рассмотрим ряд 1 1 1

■ +—+...+

который мы будем сравнивать со сходящимся рядом из примера 5.3 §5.1

1 1 1 + —+...+ 1-2 2-3 п(п+)

Поскольку * < 1 то из первого признака сравнения сле(п+1)2 п{п+У

дует, что ряд (5.13) сходится. Заметим, что сумма ряда (5.13)

выражается через число тг, а именно, S = —-1, однако вывод этого равенства выходит за рамки данного курса.

Пример 5.8. Доказать расходимость ряда

Пример 5.9. Исследовать на сходимость ряд с общим

членом

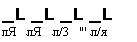+ — + — +...+—+... . (5.14)

Будем сравнивать данный ряд с гармоническим рядом

111 1

+ — + -+...+—+... ,

12 3 п

расходимость которого была установлена в § 5.1. Поскольку 1 1

~j= > ~'ТО ряд (5.14) тоже расходится.

Теорема 5.4 (второй признак сравнения). Если для рядов

(5.10) и (5.11) с положительными членами существует отличный от нуля предел отношения

ІІт^ = "' (5-15) то ряды (5.10) и (5.11) сходятся или расходятся одновременно.

Доказательство. Пусть ряд (5.11) сходится; докажем, что сходится и ряд (5.10). Выберем некоторое число v, большее, чем и. Из условия (5.15) следует существование такого номера

а.

п0, что для всех п> п0 выполняется неравенство — < v, так что

К

a<vbn. (5.16)

Отбросив первые п0членов рядов (5.10) и (5.11), что не влияет на сходимость, можно считать, что неравенства (5.16) выполняются для всех натуральных п. По условию ряд (5.11) сходится, тогда сходится и ряд с общим членом vbn. По первому признаку сходимости сходится и ряд (5.10).

Пусть теперь сходится ряд (5.10); докажем сходимость ряда

(5.11) . Для этого надо переписать условие (5.15) в таком виде

я-х° ап и

и поменять ролями ряды (5.10) и (5.11). Теорема доказана полностью.

2я + 3 и3 + Зи2 + 5п + Г

Хорошо известно, что предел ап зависит от отношения старших степеней числителя и знаменателя. Рассмотрим ряд с общим членом bn=^j = , полученным именно таким способом. После-п п

дний ряд только множителем отличается от сходящегося ряда примера 5.7 данного параграфа, поэтому сходится. Так как

lim -2= Hm ——Ц '- = 1,

„_>„с ьп я-»» 2„3 + Зи2 + 5и +1

то по теореме 5.4 сходится и исходный ряд.

Для решения вопроса о сходимости того или иного ряда обычно пытаются его сравнить с одним из «стандартных» рядов. Таким «стандартным» рядом в случае проверки сходимости служит геометрическая прогрессия, в случае же проверки расходимости гармонический ряд. Сравнение с геометрической прогрессией лежит в основе следующего часто применяемого признака сходимости.

Теорема 5.5 (признак Даламбера). Если для ряда с положительными членами at + а2+... + а+... существует такое число q < 1, что при всех п (или начиная с некоторого п) выполняется неравенство

— ^Я, (5.17)

то ряд сходится. Если же > 1 для всех или начиная с не-которого п, то ряд расходится.

Доказательство. Отбросив, если необходимо, несколько первых членов ряда, можно считать, что неравенство (5.17) выполняется для всех п = 1, 2,... . Перепишем это неравенство в виде а^.,< qan. Отсюда имеем a2<qat, а} < qa2 < q2ai, а, < qa3< q3av и т.д. Вообще, при любом п справедливо неравенство

an<qn-'av (5.18)

Это показывает, что члены рядаа, + аг+...+аи+... не превосходят соответствующих членов бесконечной геометрической прогрессии

а, + axq + axq2 +...+axq"~] +... .

Поскольку по условию 0 < q < 1, эта прогрессия сходится. В силу первого признака сравнения сходится и данный ряд.

В случае, когда s 1, имеем неравенство а^х > ап, т.е. члены ряда образуют неубьгоающую последовательность, и поэтому не выполняется необходимый признак сходимости ряда, что доказывает теорему полностью.

Признак Даламбера часто применяется в следующей предельной формуле.

Теорема 5.6. Если существует предел

im^= d, (5.19)

"л

то ряд сходится в случае d < 1 и расходится в случае d > 1.

Доказательство. Пусть d<. Возьмем некоторое число q между d и 1: d < q < 1. Из условия (5.19) следует, что, начиная

с некоторого номера п, будет выполняться неравенство <, q.

На основании теоремы 5.5 отсюда следует сходимость ряда. Случай d > 1 разбирается аналогично.

В формулировке теоремы 5.6 ничего не говорится о случае d= 1. При d= 1 возможна как сходимость, так и расходимость ряда. Например, гармонический ряд, для которого d= 1, расходится, а

ряд — +—+...+ -+... , для которого также d = 1, сходится.

Полезно заметить, что признак Даламбера дает также и оценку остатка ряда; из неравенства (5.18) следует, что

К =<*л+1 +ал+2 +ап+3+...<<7л+| + a„+xq + a„+xq2+...,

т.е.

К^т^(5.20) -q

Пример 5.10. Исследовать на сходимость ряд

, 3 З2 3я 1! 2! и!

З" Зл+| а„+] 3"+' ,3" _ 3

Имеем ап=-, °^=J—^, поэтому _ =

Очевидно, что последнее отношение будет оставаться меньше единицы для всех и > 3. По теореме 5.5 данный ряд сходится.

Мы увидим в дальнейшем, что сумма этого ряда выражается через число е, а именно, S = е1.

Пример 5.11. Исследовать на сходимость ряд

, 22 З3 и" 2! 3! и!

Имеем ап =—, ап+] = {" + 1, =(и + 1) . Составим отношеи! (п+1) п

ние последующего члена ряда к предыдущему:

лл+1 _(И + 1)" У _( 1

= 1+

и! п" V и

Поскольку предел отношения d очевидно равен числу е > 1, то по теореме 5.6 данный ряд расходится.

Пример 5.12. Доказать сходимость ряда

12 3 п + — + — +...+ — +... 2 22 23 2"

и оценить остаток Д10.

an+l п+1 и 1 п +1 (. 0,-, Имеем -^= ^+Т>=2~Г=2І я/ Предел этого отношения равен т.е. ряд сходится. Для оценки остатка ряда RXQ = аи +ап+... заметим, что если п > 10, то

£bLeI(i+iL!.i,i = 0fsi

R , a" = 2" = П I 1

10 1-9 1-0,55 2" 0,45 210-0,08 80'

Любую числовую последовательность av av an, ... можно рассматривать как функцию, определенную на множестве натуральных чисел: ап =fin), п = 1, 2,... . Следовательно, всякий числовой ряд можно представить в виде:

/(1) + /(2)+...+/(и)+.... (5.21)

В том случае, когда функция fix) монотонно убывает, может оказаться полезным следующий признак сходимости.

Теорема 5.7(интегральный признак сходимости) Пусть неотрицательная функция у =fix) определена и монотонно убывает для х>. Тогда для сходимости ряда (5.21) необходимо и достаточно, чтобы сходился несобственный интеграл

00

f(x)dx. (5.22)

і

(5.23)

Доказательство. Сходимость интеграла (5.22) означает существование предела при п -> <ю интеграла

f(x)dx.

Следовательно, сходится ряд

2 3 л

jf(x)dx + jf(x)dx+...+ jf(x)dx+... , (5 24)

Если сходится ряд (5.21), то из второго неравенства в (5.25) согласно первому признаку сравнения вытекает сходимость ряда (5.24). Обратно, если сходится ряд (5.24), то из первого неравенства в (5.25) по первому признаку сравнения вытекает сходимость ряда>(2)+У(3) +... +Ди+ 1)+..., а, значит, и ряда (5.21). Теорема доказана полностью.

Пр им ер 5.13. Выяснить, при каких а > 0 сходится ряд

1 + —+—+...+—+... . (5.26)

Положим /(х) = — (х> 1). Данная функция монотонно убывает,

ха

а

поскольку ее производная /'(*) = —отрицательна. Поэтому сходимость ряда (5.26) эквивалентна сходимости несобственного

fdx

интеграла JTЛегко проверить, что этот интеграл сходится при і х

а > 1 и расходится 0 < а < 1. Значит, и ряд (5.26) сходится при а > 1 и расходится при а < 1. Например, при а = 1,5 имеем сходящийся ряд

1 1 1

1 + + _—+...+ =+...,

2л/2 3V3 п4п а при а = 1/3 имеем расходящийся ряд

л-1

для которого интеграл (5.23) является частичной суммой. Поэтому задача состоит в том, чтобы доказать одновременную сходимость или расходимость рядов (5.21) и (5.24).

Поскольку функция fix) монотонно убывает на каждом отрезке [и, л + 1], то имеем fin +1) <fix) <fin). Интегрируя по отрезку

л+1 л+1 л+1

[я, п + 1], получаем/(я +1) Jott < f(x)dx < f(n) jdx, т.е.

л+1

Дл + 1)< f(x)dx<f(n). (5.25)

л

3. Оценка остатка ряда

Неравенства (5.25) позволяют получить оценку k-то остатка рада (5.21). Первое из них

л+1

/(n+l)S f(x)dx (я = 1,2,...) (5.27)

л

позволяет оценить сверху k-ытк остаток ряда (5.21), т.е. число Rk = /(* + 1) + /(* + 2)+... .

Чтобы получить такую оценку, достаточно сложить почленно неравенства (5.27) для всех п = к, к + I, к+ 2,... . Тогда получим § 5.3. Знакопеременные ряды

Rk < f(x)dx.

Аналогично получается оценка остатка снизу. Для этого воспользуемся вторым неравенством в (5.25), а именно,

я+1

f(x)dx<f(.n) (и = 1,2,...). (5.28)

л

Если сложить неравенства (5.28), записанные для п = к + 1 ,к + 2, к + 3, то получим jf(x)dx < Rk. В результате находим двух4 + 1

сторонние оценки остатка:

00 оо

f(x)dx<Rk<f(x)dx. (5.29)

Пример 5.14. Сколько членов ряда + —+ — +...+—+...

2 3 п

надо сложить, чтобы найти его сумму с точностью до 0,01? В данном случае /(*) = рр; оценки (5.29) дают

* + | к

Второе из этих неравенств показывает, что при Л > 100 остаток Rk не превосходит 0,01. Таким образом, для вычисления суммы ряда с требуемой точностью следует сложить 100 членов ряда, Как видим, сходимость этого ряда очень медленная.

В предыдущем параграфе изучались ряды с положительными членами. Рассмотрим теперь ряды с членами произвольного знака, или, как принято говорить, знакопеременные ряды.

1. Знакочередующиеся ряды.

теорема Лейбница

Особенно часто среди знакопеременных рядов встречаются ряды, члены которых имеют чередующиеся знаки, т.е. знакочередующиеся ряды.

Условимся считать первый член ряда положительным; тогда знакочередующийся ряд в общем виде запишется так:

ах -а2 + а3 -а4+...+(-1)я~'ая+..., (5.30)

где все ап положительны (и = 1,2, ...).

Теорема 5.8 (теоремаЛейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и стремятся к нулю, когда п -> <ю, то 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак.

Доказательство. Пусть дан ряд (5.30) и известно, что ап > ап+] для всех п и ап —► 0 при п —► оо.

Рассмотрим частичную сумму ряда (5.30) с четным числом членов

$2n =al-a2+ai-aA +...+а2п_х а2„ = = (а{-а2) + (а3 -а4)+...+(а2л_, -а2п).

В силу первого условия все разности в скобках положительны, поэтому последовательность частичных сумм {S2n} является возрастающей. Докажем, что она является ограниченной. Для этого представим в виде

Sjn = fl| -l(a2 -аъ) + (а, -а5)+...+(а2„_2 -a2n_s) + а2„].

Выражение в квадратных скобках положительно, поэтому S2n < а, для любого п, т. е. последовательность {S^} ограничена.

Итак, последовательность {S^} возрастающая и ограниченная, следовательно, она имеет предел lim S2„ = S.

л-*о0

Так как Sln+{ = S2n + а2я+і, и по условию

Й£*2»+' =0, то 1іт£2л+1 = limS2n=S.

л-»<ю л-><ю л->«

Мы доказали, что ряд (5.30) сходится и его сумма удовлетворяет неравенствам

0<S<ar (5.31)

Докажем теперь второе утверждение. Рассмотрим остаток ряда (5.30) с четным номером 2к: R2k = a2k+]агк+г+ — • ^тот ряд является знакочередующимся и он удовлетворяет всем условиям теоремы, поэтому выполняются оценки

0<Я2і<а2і+1. (5.32)

Что касается остатков ряда с нечетными номерами, то любой из них можно записать в виде Я2А+1=-а2ік+2 + а2к+г-...=-(а2к+2-a2k+i + ■■•)■ Ряд в скобках снова удовлетворяет условиям теоремы, поэтому 0 < -R2k+, < а2к+2 или

-*2**2<Я»+1<0. (5-33)

Сходимость ряда (5.30) вместе с неравенствами (5.31), (5.32) и (5.33) полностью доказывают теорему.

Пример 5.15. Доказать сходимость ряда

l-^ + -L-4+...+i=lfl+.... (5.34) 22 3і 42 п1

Сколько членов ряда надо взять, чтобы вычислить сумму ряда с точностью до 0,01 ?

Сходимость ряда следует непосредственно из теоремы Лейбница. Для вычисления суммы ряда с заданной точностью воспользуемся оценкой остатка Rk\<ak+l. В данном случае получаем

неравенство Rk | < —-—-. Таким образом, достаточно, чтобы вы-(* + 1)

1 1

поднялось неравенство ^ + ^2 "Job"' т.е. к>9. Для нахождения 296 суммы ряда с нужной точностью достаточно сложить только девять членов. Это на порядок величины отличается от случая, рассмотренного в предыдущем параграфе. Знакочередующиеся ряды сходятся быстрее, чем соответствующие ряды с положительными членами. Поэтому они удобнее для вычислений.

2. Ряды с членами произвольного знака. Плюси минусряды для данного ряда

Рассмотрим теперь ряды, члены которых имеют произвольные знаки. С самого начала условимся считать все члены ряда отличными от нуля (нулевые члены всегда можно отбросить это не отразится ни на сходимости, ни на его сумме). С каждым знакопеременным рядом

ах +аг+...+ан+... (5.35)

можно связать два ряда с положительными членами; один из них будем называть плюс-рядом, а другой минус-рядом для данного ряда (5.35). Чтобы получить плюс-ряд, следует оставить в (5.35) только положительные члены (а отрицательные отбросить); для получения минус-ряда нужно оставить только отрицательные члены ряда (5.35), сменив в них знаки на +. Например, для знакочередующегося ряда

111 (-1)"-'

1-+ +...+ -—-—+...

2 3 4 п

плюси минус-ряды соответственно имеют вид

11 111

1 + + -+... и + — + -+...

3 5 2 4 6

Любая частичная сумма Sn ряда (5.35) включает некоторую часть плюс-ряда и некоторую часть минус-ряда; поэтому

S„=S+-S^, (5.36)

где S* некоторая частичная сумма плюс-ряда и частичная сумма минус-ряда.

3. Абсолютно сходящиеся ряды и их свойства

Пусть дан знакопеременный ряд (5.35). Рассмотрим ряд, составленный из абсолютных величин его членов

Ы + Ы+-+Ы+-■ (5-37) Очевидно, что (5.37) есть ряд с положительными членами.

Определение. Ряд (5.35) называется абсолютно сходящимся, если сходится ряд (5.37), составленный из модулей его членов.

Справедливо следующее утверждение.

Теорема 5.9. Всякий абсолютно сходящийся ряд сходится. Сумма такого ряда равна разности между суммой его плюс-ряда и суммой минус-ряда.

Дока за тельство. Пусть ряд (5.35) сходится абсолютно, т.е. сходится ряд (5.37). Обозначим частичные суммы ряда (5.37) через Тп. Аналогично равенству (5.36) имеем

Тп = Т;+Тп (5.38)

Ввиду сходимости ряда (5.37) его частичные суммы Тп ограничены некоторым числом С. Тогда из равенства (5.38) следует, что Т* < С и Гл~ < С, т.е. частичные суммы плюси минус-ряда также ограничены сверху числом С. Согласно критерию сходимости рядов с положительными членами отсюда вытекает сходимость плюси минус-рядов, т.е. существуют пределы Т* = lim Tk+ и

Т~ = lim Tf. Если теперь в равенстве (5.38) перейти к пределу при

/-ЮО

п -> оо, то получим lim Тп = Т* Т~, что требовалось доказать.

Пример 5.16. Доказать абсолютную сходимость ряда

. я

» sin—

У(-1)"—(5.39) 7Т п

Составим ряд из абсолютных величин членов данного ряда:

. я

*> Sin —

£—(5.40)

я=1

Так как выполняется неравенство sin — < —, то члены ряда (5.40)

п п

не превосходят соответствующих членов сходящегося ряда Z_i „2 '

Следовательно, ряд (5.40) сходится, а ряд (5.39) сходится абсолютно.

Поскольку абсолютная сходимость ряда (5.35) означает сходимость ряда (5.37), члены которого положительны, то для установления абсолютной сходимости можно пользоваться любым из признаков сходимости из предыдущего параграфа.

4. Условно сходящиеся ряды

Определение. Ряд а, + а2+ ... + ап+ ... называется условно сходящимся, если он сходится, а ряд, составленный из модулей его членов, расходится.

Таким образом, все сходящиеся ряды можно разделить на два класса: абсолютно сходящиеся, т.е. такие, для которых ряд из модулей их членов сходится, и условно сходящиеся, для которых ряд из абсолютных величин их членов расходится.

Примером условно сходящегося ряда может служить ряд

U + I--U...+ ^+... . (5.41) 2 3 4 п

Действительно, по теореме Лейбница этот ряд сходится; в то же время ряд, составленный из модулей его членов

111 1

1 + —+ +—+...+—+... 2 3 4 п

(гармонический ряд), как известно, расходится.

Свойства условно сходящихся рядов резко отличаются от свойств абсолютно сходящихся рядов. В частности, для таких рядов не выполняется теорема 5.9, поскольку и плюси минус-ряды расходятся. Еще одно необычное свойство условно сходящихся рядов демонстрируется в следующем примере.

Пример 5.17. В условно сходящемся ряде (5.41) переставим и сгруппируем члены следующим образом:

I 2 л)Лз 6 я)+'"+І2п-1 4п-2 4пГ""

Если затем внутри каждой скобки сложить первые два слагаемых, то получим ряд

(І-І)+Гі_Ікі_!_-±к..

V2 4) 6 S) 4n-2 4п) сумма которого равна

\_ i+l_I+_L_J_+ = Ul_l+±_L+ )

2 4 + 6 8 + 10 12+"' 2І 2 + 3 4+"7

Таким образом, при перестановке членов исходного ряда (5.41) его сумма уменьшилась вдвое!

Справедлива следующая теорема, которую мы приведем без доказательства.

Теорема 5.10 (теорема Римана). Если ряд сходится условно, то в результате перестановки его членов можно получить ряд, имеющий любую сумму, а также расходящийся ряд.

Экономический пример. Баланс банка, грубо говоря, складывается из его пассивов, т.е. денег, которые он берет в кредит, и активов, т.е. денег, которые он выдает в кредит. Допустим, что у банка нулевой баланс. При этом легко привести пример, когда на счету банка находится сумма, равная его пассивам. Для этого достаточно, чтобы сроки возврата пассивов были значительно больше сроков возврата активов банка.