§ 6.3. уравнения с разделяющимися
§ 6.3. уравнения с разделяющимися
переменными.
Математические модели экономического
роста
1. Одним из наиболее простых, но весьма важных с точки зрения приложений типов дифференциальных уравнений являются уравнения с разделяющимися переменными. Это дифференциальные уравнения вида:
У =/**) • g(y), (6.8) где р(х) и giy) непрерывные функции.
в предположении, что в рассматриваемой области giy) * 0. Теперь левая часть уравнения содержит только переменную у, а правая только х Интегрируя обе части уравнения (6.9), получим
Последнее равенство запишем в виде следующего соотношения:
G{y) = Р{х) + С,
где G(y) какая-либо первообразная для а Р(х) первообразная для р(х). Таким образом, найден общий интеграл уравнения (6.8).
Пример 6.2. Найти функцию, имеющую постоянную эластичность, равную к.
По условию задачи имеем
У dx у
Отсюда, при естественном предположении х * 0, получим
dy dx
■к.
Интегрируя обе части полученного равенства, находим
1п|у| = * Щх + 1пС,
откуда следует, что
у = С ■ хк.
2. Одним из важных частных случаев дифференциальньгх уравнений с разделяющимися переменными являются так называемые автономные уравнения. Это уравнения вида
y'=g(y). (6.10)
Такие уравнения часто встречаются в различных вопросах экономической динамики. Обычно в качестве независимой переменной рассматривается время. Его отсутствие в правой части уравнения (6.10) можно трактовать как неизменность законов, по которым развивается экономическая система в рассматриваемый промежуток времени.
Если у' корень уравнения g(y) = 0, то у = y*(=const) является решением уравнения (6.10). Такое решение называется стационарным. Кроме того, отметим еще одно интересное свойство, которым обладают решения автономного уравнения.
Теорема 6.2.Еслиу = ф (х) решение автономного дифференциального уравнения, то у (р(х + С) также является решением этого уравнения.
Доказательство. Пусть у = <р (дс) решение уравнения (6.10), т.е.
<p'(x) = g(<p(x)).
Это равенство выполняется для любого х из области определения, поэтому мы можем заменить в нем х на х + С, в результате получим
<р'{х+С) = &(р(х + С)). (6.11)
Положим у = (р(х + С) ■ Принимая во внимание равенство (6.11) и правило дифференцирования сложной функции, находим
у' = 9х + С)(х + С)' = gi<p(x + C))l=g(y).
Это говорит о том, что функция у = ф(х + С) также является решением. Теорема доказана.
Замечание 1. Геометрическая трактовка данной теоремы заключается в том, что при параллельном переносе вдоль оси Ох интегральные кривые автономного уравнения переходят друг в друга.
3амечание 2. Если giy)* 0, то общее решение автономного уравнения задается формулой у = <р(х + С), где <р (х) произвольное частное решение.
3. Рассматривая ниже некоторые математические модели роста, мы будем предполагать, что в качестве аргумента неизвестной функции выбрано время /. Данные модели, базирующиеся на дифференциальных уравнениях, называются моделями роста с непрерывным временем. Отметим, что существуют также дискретные аналоги этих моделей, которые будут рассмотрены ниже.
I. Модель естественного роста (рост при постоянном темпе)
Пусть y(t) интенсивность выпуска продукции некоторого предприятия (отрасли). Мы будем предполагать, что имеет место аксиома о ненасыщаемости потребителя, т.е. что весь выпущенный предприятием товар будет продан, а также то, что объем продаж не является столь высоким, чтобы существенно повлиять на цену товара р, которую ввиду этого мы будем считать фиксированной. Чтобы увеличить интенсивность выпуска y(t), необходимо, чтобы чистые инвестиции 1(f) (т.е. разность между общим объемом инвестиций и амортизационными затратами) были больше нуля. В случае /(/) = 0 общие инвестиции только лишь покрывают затраты на амортизацию, и уровень выпуска продукции остается неизменным. Случай I < 0 приводит к уменьшению основных фондов и, как следствие, к уменьшению уровня выпуска продукции. Таким образом, мы видим, что скорость увеличения интенсивности выпуска продукции является возрастающей функцией от /.
Пусть эта зависимость выражается прямой пропорциональностью, т.е. имеет место так называемый принцип акселерации
У = ml(m = const), (6.12)
где 1т норма акселерации. Пусть а норма чистых инвестиций, т.е. часть дохода ру, которая тратится на чистые инвестиции, тогда
I = ару.
Отсюда подставляя выражение для / в (6.12), получаем у' =а тру или
у'=ку, (6.13)
где к = тар = const. Разделяя переменные в уравнении (6.13), имеем
^=kdt.
У
После интегрирования обеих частей находим
1ф| = kt + InC
или, что то же самое,
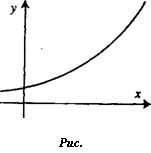 |
это следует из уравнения (6.15)) с течением времени у может принимать какие угодно большие значения, что не может не сказаться на изменении цены (в данной модели мы ее предполагали постоянной).
2. Логический рост
Рассмотрим более общий случай по сравнению с предыдущим пунктом. Пустьр = piy) убывающая функция < oj.T.e. с увеличением выпуска будет происходить насыщение рынка и цена будет падать. Проведя аналогичные рассуждения, получим уравнение:
у' = Шу> (6-16)
здесь к = la. Уравнение (6.16) представляет собой автономное дифференциальное уравнение. Так как к > 0,р > О, у >0, то из (6.16) следует, что y(t) есть возрастающая функция [у' > 0). Исследуем y(t) на выпуклость. Дифференцируя уравнение (6.16) по t, получим
У" = ку{ау'У + Р
или
'dp у
dy р
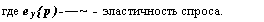
Если y(t0) = у0, то из (6.14) следует, что С = у^Т**, т.е.
у = у0ек('-'0). (6.15)
Уравнение (6.15) называется уравнением естественного роста. Этим уравнением описываются также динамика роста цен при постоянном темпе инфляции, процессы радиоактивного распада и размножения бактерий.
Замечание 3. Модель естественного роста целесообразно применять на начальных этапах развития экономической системы в течение ограниченного промежутка времени, поскольку (как т.е.
(6.17)
у" = кур 1-Х
V eyJ
dy_ р_ dp у
Из (6.17) вытекает, что если спрос эластичен, т.е. е\> 1, то У > 0, т.е. функция спроса выпуклая функция, а если спрос неэластичен, т.е. е | < 1, то у" < 0 и функция спроса вогнутая функция.
Пусть, например,piy) = b-ay (a, b>0), тогда уравнение (6.17) принимает вид:
Отсюда получим, что
у' = к(Ь ау)у.
(6.18)
у =
Cbe"
1 + Сде*
(6.19)
Из (6.18) легко получить, что / = 0, если у = 0, или у = —, а
а
также, что/' < 0 при у = —,иу" >&при у > — (рис. 6.5).
 |
График функции (6.19) называется логистической кривой. Она также описывает некоторые модели распространения информации (рекламы), динамику эпидемий, процессы размножения бактерий в ограниченной среде обитания и др.
Замечание 4. Из графика логистической кривой видно, что при малых t логистический рост схож с естественным ростом, однако при больших / характер роста меняется, темпы роста замедляются и кривая асимптотически приближается к прямой
у = —■ Эта прямая является стационарным решением уравнения а
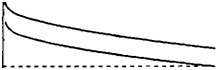
(6.18) и соответствует случаю р(у) = 0. Для уравнения (6.18) также существуют решения и при у>~~, имеющие графики (рис. 6.6).
dy
y(b ay)
В данном случае довольно легко получить и явное выражение для y(j). Разделяя переменные в уравнении (6.18), находим
= kdt,
Ъ/а
или
О
т.е.
■ = Сек
b y b-ay J Проинтегрировав это соотношение, имеем ln|y|-ln|&-qy|=tt/ + lnC,
у
b-ay
Рис. 6.6
Но, так как в этом случае р{у) < 0, то эти графики не имеют экономической интерпретации.
Замечание 5. Более реалистичной является модель, в которой скорость роста зависит не от дохода, а от прибыли. Пусть С(у) = ау +/? издержки (a, fi константы) тогда
y' = Hpiy)y-<*y-fi(6-20)
При этом интегральные кривые, удовлетворяющие начальному условию y(t0) = у0>у*, будут асимптотически приближаться к у* на + оо, а интегральные кривые, удовлетворяющие условию У(*о) к У*■> будут асимптотически приближаться к у* на -оо (рис. 6.8).
в) D > 0. В этом случае существуют два стационарных решения у=у{, у-уг (0 < У] к Ут)При этом у > 0 при ух<у <у2, и У < 0 триу<у1 нпиу>у2 ( рис. 6.9).
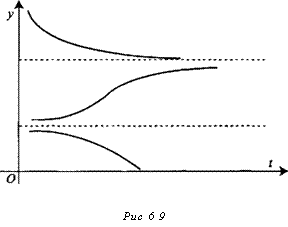 |
о
t
Рис 6 7
Еслиріу) = bау, то правая часть уравнения (6.20) представляет собой квадратный многочлен относительно у с отрицательным коэффициентом перед у2. В этом случае возможны три варианта.
а) D< 0. Следовательно, у' < 0. Издержки настолько велики,
что это приводит к постоянному падению уровня производства и
в конце концов к банкротству (рис. 6.7).
б) D = 0. В этом случае У < 0 и имеется одна стационарная кривая
Предлагаем читателю самостоятельно проинтегрировать уравнение (6.20) (при р(у) = bау) и получить явные выражения для у.

Рис 6 8
3. Неоклассическая модель роста
Пусть У = F(K, L) национальный доход, где К объем капиталовложений (фондов), L величина затрат труда, F(K, L) линейно-однородная производственная функция (F(tK, tL) = tF(K, L)). Пусть fljt) производительность труда:
где к = KJL фондовооруженность. Как известно, f (к) > f'(k)<0.
Предполагаем, что:
происходит естественный прирост трудовых ресурсов, т.е.
L' = aL(a = const);
Инвестиции направлены как на увеличение производственных фондов, так и на амортизацию, т.е.
L'=K'+0K (6.21)
(fi -норма амортизации).
Пусть / норма инвестиций (т.е. / = /У), тогда
IY=K' +/9К=> К' = IY-/3 К. (6.22) Из определения фондовооруженности вытекает
іп*=ш:-іпі.
Дифференцируя эти соотношения по /, получим
k~ К L
Подставляя сюда значения для V и 1С из (6.21) и (6.22), находим
*' IY-PK
— = а,
к К
т.е.
к' = ^-(в+а)к = !£-(в+а)к. у
Учитывая, что / = —, получим L
k=lf(k)-(a +/?)*. (6.23) Уравнение (6.23) называется уравнением неоклассического роста.
Замечание 6. У автономного дифференциального уравнения (6.23) существует стационарное решение к = к*. Действительно, так как /"(к) < 0, то графики If (к) и (а +/3)к обязательно пересекутся (рис. 6.10).
О
Рис. 6.10
Кроме того, так как f'(k) непрерывная монотонно убывающая функция, то существует такое і,, что f'(k])= (а + $ (т.е. у
k{t) существует точка перегиба). Итак, при к > к* имеем к < 0; при к < к* будет к > 0. При к < кх имеем к" > 0, а при к > kv к" < 0.
Ввиду этого интегральная кривая уравнения (6.23) очень напоминает логистическую кривую (рис. 6.11).
■f
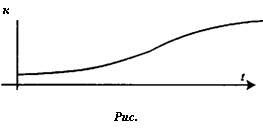 |
Обсуждение Математика в экономике Часть 2
Комментарии, рецензии и отзывы
