§ 6.4. некоторые простейшие методы интегрирования дифференциальных уравнений

§ 6.4. некоторые простейшие методы интегрирования дифференциальных уравнений

1. С одним из методов интегрирования дифференциальных уравнений мы уже познакомились в предыдущем параграфе, это -метод разделения переменных. В данном параграфе мы рассмотрим еще несколько методов, один из которых метод вариации постоянных применяется для решения так называемых линейных уравнений.

Определение 6.4. Дифференциальное уравнение вида ф)у'+Ах)у+ у{х) = 0 (6.24)

называется линейным дифференциальным уравнением первого порядка.

Если а(х) * О, то уравнение (6.24) можно преобразовать следующим образом:

У'+ Р(Ф = Ах), (6-25)

Дифференциальное уравнение

у'+р(х)у = 0 (6.26)

назьтается линейным однородным уравнением, соответствующим уравнению (6.25).

Уравнение (6.26) представляет собой уравнение с разделяющимися переменными. Из (6.26) следует

± = -р(х)ах. У

Интегрируя это уравнение, получим 1пу = -Р(х) + пС,

где Р(х) произвольная первообразная для функции р(х), а С -положительная постоянная. Из последнего уравнения находим общее решение уравнения (6.26):

у = Се-р(х), (6.27)

где С постоянная произвольного знака.

Теперь будем искать решение уравнения (6.25), положив в формуле (6.26) С = С(х), т.е. заменяя константу С на некоторую (искомую) функцию (отсюда и название метода метод вариации

произвольной постоянной). Итак, полагаем у = С(х)е'Р(х). Отсюда получим

у = се-ям Се-Юріх). (6.28)

Подставляя выражения для у и у' из (6.27) и (6.28) в (6.25), находим

Се-*йСе-р^р(х) + р(х)Се-рЫ= fix). Отсюда получим, что

С=Ах)еЪ

Следовательно, С(х)= ^f(x)eP{x)dx. Подставив в (6.27) выражение для С(х), получим общее решение уравнения (6.25). Пример 6.3. Решить уравнение

х

Это линейное дифференциальное уравнение. Соответствующее однородное уравнение имеет вид

у' + 2^= 0. х

Разделяя переменные, имеем

dy 2dx у x

С

Откуда 1п[у = -21п|дг| + In С, т.е. у = —-.

X

Полагая теперь С = С(х), находим

С'(х) 2С(х)

У х2 xі "

Подставив выражение для у и у' в исходное уравнение, получим

СЧ£)_2С(х) + 2С(х) 2 х2 xі xі

Отсюда следует, что С(х) = 5х*. Значит, С(х) = Xs + С, (С, = const).

Таким образом, у(х) = * +С| или у(х) = х3 +

х х2

Одним из часто используемых методов интегрирования дифференциальных уравнений является отчасти известный нам из интегрального исчисления метод замены переменной (подстановки). Например, уравнение Вернути

заменой Z = ух~п приводится к линейному. Пример 6.4. Решить уравнение

У~У = у

Выполнив замену z = у5, получим z' = Ъу^у'. Умножив обе части исходного уравнения на Ъу2 (*0), с учетом выражений для z и z' находим

z' 3z = Ъе6*.

Соответствующее линейное однородное уравнение z' 3z = О имеет решение z Се3*. Применяя метод вариации произвольной постоянной, получим

С'(х)еіх+ЗС(х)еьЗС(х)еіх = Зе6*, т.е. Cx)f=3eix, С{х) = еь + С,, где С,произвольная постоянная.

Таким образом, z = е^+С^Ч Значит, у = ^е6х +С,е3*.

Метод замены применим и к так называемым однородным уравнениям первого порядка. Это дифференциальные уравнения вида

/-/(?)• <"»>

Подстановкой у{х) = хм(х) они приводятся к уравнениям с разделяющимися переменными. Действительно, у' = и(х) + хи' (х). Ввиду этого уравнение (6.29) принимает вид

и + хи' = J{u).

Разделяя переменные, получим

du _dx f(u)-u х '

Отсюда находим общий интеграл уравнения:

du

if [и]-и

После нахождения и(х) необходимо вернуться к функции у(х) = хи(х).

Замечание 1. Если существуют корни уравнения Ди) и, ток найденным решениям добавляются стационарные постоянные решения и(х) = и* где м* любой корень уравненияДи) = и.

Пример 6.5. Решить уравнение

7

MS-liJ ■ (6'30)

(6.31)

Это уравнение является однородным. Выполнив замену у(х) = хи(х), приходим к уравнению

2и-и2x

t du tax >2u-u2Jx'

Разделяя переменные, получим при и * 1

du tax

или

1

M-l

= ln|x| + C,

M = (ln|x| + C)-,+l 

Кроме этого, у уравнения (6.31) имеется стационарное решение и(х) = 1. Таким образом, решением исходного уравнения (6.31) являются функции § 6.5. Линейные дифференциальные уравнения высших порядков

1. в предыдущем параграфе мы научились решать линейные дифференциальные уравнения первого порядка. в данном параграфе мы рассмотрим обобщение этого класса уравнений на случай уравнений более высоких порядков.

Определение 6.5. Дифференциальное уравнение п-го порядка называется линейным, если оно имеет вид

У") + a,(x)y"-')+ a2(x№"-V+...+ аП(х)у =/*), (6.32)

где <3|(х), а2(х),ап(х), fix) непрерывные функции.

Имеет место следующая

Теорема 6.3 (существования и единственности). Пусть функции а{(х),an(x), fix) непрерывны на отрезке [а, Ь]. Тогда существует, причем единственное, решение у(х) уравнения (6.32), удовлетворяющее начальным условиям у(х0) = у0, у'(.х0) =yQ'...., У<п-]Чх0) = у0^гдех0е(а, Ь).

Примем эту теорему без доказательства. в то же время отметим, что если в теореме Коши утверждалось существование и единственность решения локального, т. е. решения в некоторой окрестности точки, то в данной теореме утверждается существование и единственность решения линейного уравнения на всем промежутке [а, Ь], т.е. утверждение теоремы носит глобальный характер.

Обозначим через L{y):

i(y)=y-) + fllWy-')+ ... +ая(х)у. (6.33)

Заметим, что выражение такого вида называется линейным дифференциальным оператором п-го порядка. Отметим свойство оператора L(y), необходимое нам в дальнейшем.

Лемма 6.1. Пустьу{(х) и у2(х) произвольные функции, имеющие производные до п-го порядка включительно, ctuc^произвольные константы, тогда

Цс^+с^) = с,Цу,) + c2L(y2). (6.34)

Справедливость этого утверждения легко установить непосредственной проверкой.

С учетом наших обозначений уравнение (6.32) может быть записано в виде

L(y) =fix). (6.35)

Уравнение

L(y) = 0 (6.36)

называется линейным однородным уравнением, соответствующим уравнению (6.35). в противоположность этому уравнению (6.35) (при fix)sO) называется неоднородным. Следующее утверждение связывает решения уравнений (6.35) и (6.36).

Теорема 6.4. Общее решение неоднородного уравнения (6.35) есть сумма частного решения у (х) этого уравнения и общего решения соответствующего ему однородного уравнения (6.36).

Доказательство. Покажем сперва, что сумма у (х) и произвольного решения у Ах) однородного уравнения также является решением уравнения (6.35). Действительно, в силу леммы имеем

Д у +у0) = Цу) + L(yQ) = fix) + О =fix),

что и требовалось доказать. Теперь нам остается доказать, что всякое решение у(х) неоднородного уравнения есть сумма у (х) и некоторого решения yQ(x) уравнения (6.36). Имеем

L(y-y) = L(y)-L(y) = fix)-fix) = 0.

Следовательно, j>0(jc) =у(х) у (х) решение уравнения (6.36), значит, у(х) -у0(х) + у (х), что и завершает наше доказательство.

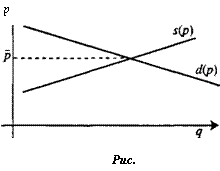
Пример 6.6. Рассмотрим уравнение Самуэльсона

p'=k(d(p)-s(p)), (6.37)

моделирующее связь между изменением цены р и неудовлетворенным спросом d(p) s(p) (здесь d(p) и s(p) соответственно величины спроса и предложения при цене р, к>0). Предположим, что спрос и предложение задаются линейными функциями

d(p) = a-bp, s(p) = т + пр, (6.38)

где а, Ь, т,пнекоторые положительные числа. С учетом (6.38) уравнение (6.37) примет вид

р'= к(п Ь)р ±к(а + т). (6.39)

Уравнение (6.39) является линейным дифференциальным уравнением. Найдем решение соответствующего ему однородного уравнения. Имеем

^= k(n-b)dt; Р

lnp = k(n-b)t + In С;

p(t) = Ce^'. (6.40)

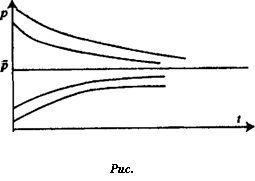
В качестве частного решения уравнения (6.39) можно использовать стационарное равновесное решение p(t) = р = const, где ркорень уравнения d(p) = s(p) (в этом случае обе части уравнения (6.37) будут равны нулю). Из (6.39) нетрудно найти, что

~р=тй (рис-6-12>-

Рис. 6.13

Если п = Ь, то pit) = const (рис. 6.14).

rfO-fpW"-*. (6.41) b + n

Из (6.41), в частности, вытекает, что если п > Ь, то с течением времени интегральные кривые будут отдаляться от состояния равновесия р (рис. 6.13).

Рис. 6.14

Данную модель можно рассматривать как непрерывный аналог паутинной модели рынка.

3. Отметим одно важное свойство линейных уравнений, часто используемое при нахождении решений.

Теорема 6.5. Пусть ух(х) uyJx) соответственно решения уравнений L(y) =/i(x) и L(y) =J2(x), тогда yt(x) + у2(х) есть решение уравнения

АУ) =/;(*)+/2оо.

Действительно, Цу1+у2) =L(yx) + L(y2) =/х(х) +/2(х), что и утверждалось в теореме.