§ 6.7. линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

§ 6.7. линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данный параграф посвящен нахождению решений линейных дифференциальных уравнений второго порядка. Однако следует заметить, что многие результаты этого параграфа могут быть без труда перенесены на случай линейных уравнений высших порядков.

1Начнем со случая однородного уравнения.

Нахождение общего решения линейного однородного уравнения требует знания какого-либо фундаментального набора решений. Последнее в общем случае является довольно сложной задачей. Однако эта задача намного упрощается, если коэффициенты уравнения постоянны. Рассмотрим уравнение

y"+py' + qy = 0, (6.49)

где q, р некоторые константы.

Будем искать решение уравнения (6.49) в виде функции у = е**. Дважды дифференцируя эту функцию, получаем у' = Ае**, у" = А2еъ. Подставляя эти выражения дляу, у' и у" в уравнение (6.49), имеем

А2еь + рАе** + qeu = 0. (6.50) Так как еи Ф 0, то это соотношение эквивалентно уравнению A2+pA+q = 0. (6.51)

Определение 6.8. Алгебраическое уравнение (6.51) называется характеристическим уравнением линейного однородного дифференциального уравнения (6.49).

При решении характеристического уравнения могут возникнуть три случая.

Случай 1. Дискриминант D характеристического уравнения (6.51) больше нуля. Тогда существует два действительных и различных решения х, и х2 уравнения (6.51). Соответствующие

им решения ух = е^х, у2 = еХгх линейно независимы. Действительно, их определитель Вронского

= (А2-А1)е(М+Ъ)х

У

ввиду того, что Х^Х2, отличен от нуля. Следовательно,^! иу2 образуют фундаментальный набор и общее решение уравнения (6.49) имеет вид

= Qe*X + С,е*2Х.

Пример 6.8. Решить уравнениеу+у -2 = 0. Корнями характеристического уравнения А2 + А 2 = 0 являются числа Я, = 1 и А2 = -2. Следовательно, общее решение уравнения имеет вид у = Схех+С2е-Ъ.

Случай 2. Z) = 0. У характеристического уравнения суще-ствует единственный корень л = ~~^і< которому соответствует

решение ух = ег**. Но для построения общего решения нам необходимо еще одно линейно независимое относительно >>, решение уравнения (6.49). Покажем, что таковым является функция^ = хе**. Действительно, у2 = А хе^ + е**, у"2 = А2хеъ + 2АеЛх. Подставляя выражения для у, У и у" в уравнение (6.49), имеем

е**[х(А2 + pA + q) + 2A + p) = 0. Учитывая, что А является корнем уравнения (6.51) и при этом

П

А = -у, мы видим, что последнее равенство выполняется тождественно, т.е. у2 решение уравнения (6.49). Покажем теперь, что ух и у2 линейно независимы. Имеем

= е2Ах.*0.

е** хе* Ае^ (1 + Ах)еъ

Следовательно,_у, иу2линейно независимы и образуют фундаментальный набор. Таким образом, общим решением в этом случае будет

у = е^(С1 + С2х).

Пример 6.9. Найти общее решение уравнения у" + 6у + 9 = 0.

Характеристическое уравнение А2 + 6А + 9 = 0 имеет единственный корень А = -3. Поэтому общее решение имеет вид: у = ег*(С1 + С2х).

Случай 3. D<0, т.е. р2 4q < 0 или ^-<q. Прежде всего, сделаем замену y = eaxz и подберем а так, чтобы для новой функции z получилось уравнение, не содержащее члена с z'. Имеем

y'=eaxz + eaxz у"= сРе"^ + aeaxz'+ aeaxz' + eaxz". подставляя эти выражения в уравнение (6.49), получим уравнение e^z" + (р + 2a)z'+ (о2 + pa+q)z) = 0.

Чтобы обеспечить отсутствие слагаемого с г', положим <з = --j. Тогда получим уравнение

z" + (а2 +ра +q)z = 0. Подставляя а = -у в выражение а2 + pa + q, получим

2 2 q

— + <7 = > 0. Обозначим это выражение через fi2.

4 2 4

Итак, уравнение для z приобретает вид

z" + fi2z = 0.

У этого уравнения имеется два линейно независимых решения

z, = cos fix,z2 = sin fix.

Соответственно для уравнения (6.49) получаем решения

ух = еш cos fix, у2 = ет sin fix, (6.52)

которые остаются линейно независимыми. Итак, в случае £><0 имеем фундаментальный набор из двух решений (6.52), где

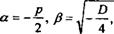
общее же решение имеет вид

у = e^C^cos fix + C2smSx).

Замечание. Числа а и fi имеют простой смысл в теории комплексных чисел. В случае D < 0 характеристическое уравнение (6.51) имеет два комплексно сопряженных корня

^=-f±^/ = a±/Jf,

следовательно, а и fi суть не что иное, как действительная часть и коэффициент при і в выражении для X.

358

Пр им ер 6.10. Решить уравнение у" 2у'+ 2у = 0.

Корнями характеристического уравнения X2 2Л + 2 = 0 будут Л, 2 = 1 ± і. В данном случае а ~ 1, fi = 1, так что общим решением данного дифференциального уравнения будет

у = e*(C,cos х +C2sinx).

2. Рассмотрим теперь неоднородное уравнение

y+py'+qy = А*)(6-53)

Для отыскания решения этого уравнения так же, как и в § 6.4, мы можем применить метод вариации постоянной, т.е. искать решение в виде

y = Ci(x)yl + C2(x)y2, (6.54)

гдеух(х),у2(х) фундаментальный набор решений соответствующего однородного уравнения, а С,(х), С2(х) искомые функции. Из (6.54) находим

У' =C'y]+C2'y2+Ciy]'+C7y2'.

Потребуем дополнительно, чтобы

С^+С2'у2=0. (6.55)

Тогда мы получим у' = Сух + С^'. Следовательно, /'= С/у,' + С2'у2' + С>," +С2у{. Подставляя найденные значения для у, у' и у" в уравнение (6.53), имеем

С,(УГ+ ДУ/ + qyx) + С2(у2" + ру2' + ©ъ) + С,>/ + С2>2' = /х).

Оба выражения, заключенные в скобки, равны нулю, так как ух и у2 являются решениями однородного уравнения (6.49). Следовательно, мы получим уравнение С,'у,' + C2yJ Ах)Таким образом, неизвестные функции С{ и С2 должны удовлетворять системе уравнений

|Оу,+сі>2=о

Определителем этой системы является определитель Вронского, который отличен от нуля в силу линейной независимости у, и у2. Следовательно, из системы (6.56) мы можем однозначно оп359

Подставляя полученные выражения в исходное уравнение, имеем

2Ле* = е*; А =0,5.

Таким образом, общим решением данного уравнения является

у = (0,5х2 + С1х + С2)ех.