11.2. функции спроса на факторы (ресурсы) в случае долговременного промежутка

11.2. функции спроса на факторы (ресурсы) в случае долговременного промежутка

В связи с тем, что, как правило, /(х(,0)=/(0,х2)=0 (т.е. если хотя бы один ресурс не затрачивается (не используется), то объем выпускаемой продукции равен нулю), экономически осмысленными являются векторы (х|5х2) затрат ресурсов, для которых х(>0, х2>0. Поэтому в случае долговременного промежутка задача максимизации прибыли представляет собой обычную задачу на глобальный абсолютный максимум при х,>0 и х2>0. Из математического анализа известно, что точки локального абсолютного максимума следует искать только среди точек (хгх2), которые удовлетворяют системе уравнений

аРЖх,,^) dPR(xvx2)_n дх{ ' дх2

или, в развернутом виде (ибо прибыль PR(xr х2) = pj[x{, х2) -(ptx + p2x2)),

dflxx) dfix ,х2)

a2M,x2)

дххдх2

Если вторые частные производные производственной функции J[xrx2) при всех х;>0, х2>0 таковы, что

а2лх1д2)<о а2(х,,х2) д2лхЛ)

дх2 дх2 дх]

(эти неравенства несколько сильнее условий 2" и 3 раздела 11.2 главы 10, посвященной производственным функциям), то график производственной функции y=J[xvx2) в трехмерном пространстве Ox,x,j> есть поверхность, выпуклая вверх. Следовательно, график прибыли PR(xr х2), получаемый путем вычитания из графика функции pj{xvx2) плоскости у = p{xt + р2х2, являющейся графиком издержек производства, имеет вид "шапочки", у которой есть "макушка". "Макушка" соответствует глобальному максимуму прибыли:

PR(xt, х2) = pj[xy, х2) (р]х1 + р2х2).

Из этого геометрического факта следует, что система (1) имеет единственное решение (х,0, х2°), которое является точкой не только

у

О

Z

Рис. 11.2а

Рис. 11.26

локального, но и глобального (искомого нами) максимума прибыли PR(xv х,). Вектор (х,и, х,°) затрат ресурсов, который является решением задачи максимизации прибыли PR(xr х2) = pj[xt, х2) (р х, + р2х2), называется локальным (частичным) рыночным равновесием фирмы (в случае долговременного промежутка).

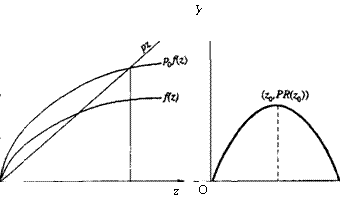
Рисунок графика прибыли PR(xr х2) в трехмерном пространстве, вообще говоря, достаточно сложен. Поэтому график прибыли представим схематически на плоскости Ozy, где координатная ось Oz изображает плоскость Ох,х2. Нарис. 11.2а даны графики производственной функции f{z), дохода фирмы pj[z) и издержек производства pz. На рис. 11.26 изображен график прибыли PR(z) — pjiz) pz, который получен вычитанием из графика дохода фирмы pj[z) графика издержек производства pz. Точка PRiz^) есть "макушка" "шапочки" графика функции PR(z) = pjiz) PZПодставив вектор (х,°, х,°) в уравнение (1), получим тождества

дх,

=Pv Л

ЭДх, ,х2) дх2

=Р2,

(2)

откуда путем почленного деления первого тождества на второе получаем

ЭДх, ,х2) ах, _рх

адх^,х») ~7г

дхг

Проведем через точку (х,°, Xj0) изокванту и изокосту, которые эту точку содержат. Уравнение изокванты имеет видДх,, х2) = у0, где yQ = =Дх,°, Xj°). Уравнение изокосты имеет вид ptx. + р^ = С0, где С0 = = ptx° + PjXj0. Перепишем уравнение Дх,, Xj) = у0, выразив явно переменную Xj через переменную х,, т.е. в виде х, = А(х,) (обратим внимание, что уравнения /х,рс2) = у0и х2 = й(х,) формально разные, но они аналитически описывают одну и ту же изокванту / см. рис. 11.3).

tg q> =

dh(xb

9Лх,0,х2°)

Эх,

/

ЭДх, л)

Эх,

(4)

Из математического анализа известно, что для изокосты Pi

+ PjX2=C0 отношение — = tg у/. Из (3), (4) и (5) следует, что tg q> =

= tgy, что означает, что касательная А" к изокванте в точке (х.°, х2°) совпадает с изокостой, т.е. в точке (х,°, х2°) изокванта обязательно касается изокосты А" (см. рис. 11.3). Получена важная (подчеркиваем это особо!) геометрическая характеристика локального рыночного равновесия (х,°, х2°) фирмы касание в этом равновесии изокванты и изокосты.

Отметим, что, приступая к решению задачи максимизации прибыли, мы не имели конкретных изокванты и изокосты, которые касаются друг друга в точке (х,0, х2°), ибо не имели самой этой точки. Касающиеся друг друга изокванта и изокоста появляются после того, как аналитически найдено локальное рыночное равновесие (х,0, х,°) путем решения системы уравнений (1).

Левая (' четырехэтажная") дробь в (3) есть не что иное, как Rn{x^,x2) предельная норма замены первого ресурса вторым в точке (х,°,х20).

Равенство (3) выражает следующий фундаментальный факт теории фирмы:

в точке локального рыночного равновесия (х.°,х2°) предельная нррма замены /?12(х,0,х2°) первого ресурса вторым равна отношению — рыночных цен на эти ресурсы.

2 Поскольку х,0 и х2° получаются в виде решения системы уравнений (1), постольку х,0 и х2° есть функции цен (р0, pv р2), т.е.

x?=d{{pu,pvp2), x2°=d2(p0,prp2). (5)

Выражения (5) называются функциями спроса на ресурсы (затраты). Их зндчения х,0 и х2° выражают оптимальные выборы затрат (использования) ресурсов как функции цены выпускаемой продукции и цен на ресурсы.

Подставив функции (5) в производственную функцию y—f{xv х2), получим выражение

/=/Ц(/>,,'/>, Л)> di(PvPi P2))=s{p0,p] ,р2),

которое называется функцией предложения выпуска.

Функции спроса на ресурсы и функция предложения выпуска являются однородными нулевой степени по всем своим аргументам р0, />, и р2, т.е. dt(tp0, tpv tp2) = dx{pu, pv p2), d2(tpQ, tpv tp2) = d2(p0, pv p2), s(tp0, tpt, tp2) = s(pQ, pv p2) для любого числа t > 0. Свойство однородности означает, что одновременное изменение всех цен pQ, pv р2 в одно и то же число раз t (т. е. при изменении масштаба, но не структуры цен) не меняет х.°, х2° и у°, что важно с содержательной точки зрения. С математической точки зрения однородность нулевой степени функции спроса и функции предложения является простым фактом, ибо максимизация прибыли PR(x{,x2) = tpj{xvx2) -(tp^x^ + tp2x2) сводится к системе уравнений (2), поскольку на множитель t > 0 можно сократить.