11.4. комбинация ресурсов (факторов производства), максимизирующая объём выпуска при ограничении на затраты

11.4. комбинация ресурсов (факторов производства), максимизирующая объём выпуска при ограничении на затраты

Для случая долговременного промежутка рассмотрим задачу максимизации объема выпускаемой продукции при ограничении затрат на приобретение ресурсов (факторов), т.е. рассмотрим задачу 1:

Л*,, х,) -> max (7)

при условии, ЧТО

р^+Ргх2<К х, > 0, х, > 0.

(8) (9)

Величина К не обязательно равна величине С0 (см. раздел 11.2). Решение этой задачи математического программирования допускает наглядную геометрическую интерпретацию (см. рис. 11.5). Ограни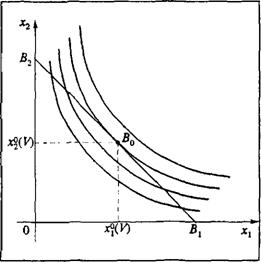

чениям (8) и (9) соответствует треугольник ОВ1В2 плоскости OxxxY Максимизация функции (7) геометрически соответствует тому, что мы переходим на все более "северо-восточные" изокванты, пока они имеют еще общие точки с треугольником OBtB2 (прямая В1В2 имеет уравнение /?,х, + р2х2 = У). Изокванты гладкие линии, выпуклые к точке О (а это так, ибоДх,, х2) не произвольная функция двух переменных, а производственная функция, т.е. функция, удовлетворяющая определенным требованиям гладкости и выпуклости), поэтому решению задачи (7), (8), (9) соответствует изокванта, которая касается гипотенузы (изокосты) ВХВ2 в точке В0. Любая изокванта, расположенная "северо-восточнее" этой изокванты, содержащей точку В0, не подходит, ибо не имеет общих точек с треугольником ОВЖ. Координаты х°(V) и х2 V) точки В0 и дают решение задачи (8), (9), (10).

В связи с тем, что это решение (х,°( У), х2°( V)) обращает ограничение (8) в равенство /j,*,0 + р2х2° = V, вместо задачи (7), (8), (9) можно рассмотреть более простую задачу на условный экстремум

Дх,, Xj) -» max (7)

при наличии офаничения

Р>хх Ргхі = V (10) (х,>0,х2>0), КШ)

заданного в виде равенства.

Задачи (7), (8), (9) и (7), (10) разные, но решение (хДІО.хД У)) У них одно и то же (в случае отсутствия так называемых угловых решений, которые здесь не рассматриваются). Поскольку сумма р1х1+р1х2 равна издержкам производства, постольку целесообразно заменить К на С и формально перейти к задаче максимизации объема выпускаемой продукции для случая долговременного промежутка при фиксированных издержках производства С (величина Сифа-ет роль параметра и не обязательно равна величине С0 (см. раздел 2)):

Дх,, хг) -» max (7)

при условии, что

Р1Х1+Р2Х2=С (И)

(х,>0,х2>0). 1 '

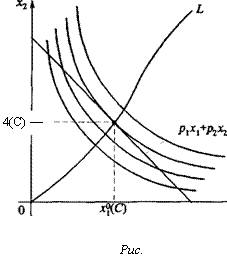
Геометрическое решение задачи (7), (11) также наглядно очевидно (см. рис. 11.6): следует переходить на все более "северо-восточ-

ные" изокванты до тех пор, пока они продолжают иметь общие точки с изокостой, соответствующей фиксированным издержкам производства С. Ясно, что решением задачи максимизации выпуска будет точка (хДС), x2(Q) касания последней из допустимых изо-квант и фиксированной изокосты рххх + p^2 = С. Эта точка касания зависит от величины издержек производства С (поэтому и написано (х,0(С), х2°(С)). Если издержки производства С изменятся, то изменится, вообще говоря, и точка (xx°(Q, x2°(Q). Множество точек (хДО, x°(Q), соответствующих различным значениям С, образуют линию Г (см. рис. 11.6), которая называется долговременной линией развития фирмы. Точка (х,°,х2°) локального рыночного равновесия фирмы (см. раздел 11.2) обязательно принадлежит линии L.

Решим задачу (7), (11) формально с помощью функции Лагранжа

Цхх,х2,Х) =Лх1,х2) + X(C-ptxx р2х2).

Для функции Лагранжа выписываем систему уравнений

дх.

дЦх1гх2,) dL(xt,x2,X)_Q dL(xvx2,X)=Q

дх,

или в развернутом виде

dfixvx2) dftx х2)

дх,

дх.

Критическая точка (х 0(С),х2и(С)Д0(С)) функции Лагранжа, удовлетворяющая системе (12) и взятая без последней координаты (множителя Лагранжа) Х°(С), т.е. точка (х°(С),х2и(С)), и есть решение задачи (7), (11) максимизации выпуска при данных фиксированных издержках производства С. Подставив точку (х|°(С),(х2и(С)Ди(С)) в первые два уравнения системы (12), получим два тождества. Поделив почленно первое тождество на второе, получим, очевидно, выражение (3) (множитель Лагранжа Х°(Q сократится). Получили аналитическое обоснование того, что в точке (х°(С),х,0(С)) изокванта и ■ изокоста касаются (см. рис. 11.6). Вообще говоря, критическая точка функции Лагранжа, взятая без последней координаты, не обязана быть решением задачи (7), (11) на условный максимум. В случае же производственной функцииДх^х,), удовлетворяющей определенным требованиям гладкости и выпуклости, критическая точка функции Лагранжа (без последней координаты) есть решение задачи (7), (11) на условный экстремум. Отметим также, что в случае производственной функции Дх,,х,) x,°(C)>0, x2°(C)>0, X°(Q>0.

В разделе 11.2 в точке'локального рыночного равновесия (х,0^0) были определены издержки производства С0 = /^х,0 + р2х2и. Если в ограничении (12) положить С= С0, то несложно показать, чтохДСд)

1

= X,0, х"(С0) = х2и, а также Jo^j — Р0, т.е. величина, обратная

множителю Лагранжа Х°(Са), равна рыночной цене pQ единицы выпускаемой фирмой продукции. Таким образом, предложена естественная экономическая интерпретация множителя Лагранжа Х°(С0). Подставив x|°(Q, х2'(С) в выражение у =Дхр х2), получим, что

y=Axl0(Q,x1°(Q) = F{Q, (13)

т. е. получим у = F[Q как функцию издержек производства С, а не как функцию у =.Дхрх2) объемов х, и х2 затрачиваемых (используемых) ресурсов. Выражение (13) называется значением задачи (7), (11).

Так построенная функция у = F Q соответствует случаю долговременного промежутка.

Имея функцию у = F(Q, можно выписать выражение для прибыли в терминах издержек производства PR(Q — p0F(Q С (сравните с выражением для прибыли фирмы в терминах затрачиваемых (используемых) ресурсов см. раздел 11.1).

Задача максимизации объема выпускаемой продукции при фиксированных издержках производства С для случая краткосрочного промежутка, когда лимитирован объем х2* второго ресурса, имеет вид

Axr х2") -> max (14)

при условии, что

'Л1!$ьшС ,,5)

Ограничимся наглядным геометрическим решением задачи (7), (14) (см. рис. 11.7). ^

Перемещаемся по изоквантам на "северо-восток" до того момента, пока изокванта не пройдет через точку (x"(Q,x2*), которая и есть решение задачи (14), (15). От этой изокванты далее на "северо-восток" идти нельзя, ибо в точках у = (yt,y2) пересечения новых изоквант и фиксированной изокосты рх + р2х2 = С имеет место неравенство у2 * х2 (см. рис. 11.7).

Если бы условия х, = х2# не было, то решением задачи максимизации объема выпускаемой продукции была бы точка (х,°(С),х2и(С)) (см. рис. 7), которая соответствует случаю долговременного промежутка. Очевидно,ДхДСХхД С)) >Дх,*(С), х,*), ибо изокванта, проходящая через точку (x|°(Q,x2°(C)), расположена "северо-восточнее" изокванты, проходящей через точку (x"(Q,x2).

Получен важный результат теории фирмы:

при одних и тех же издержках производства Собьем выпускаемой продукции для долговременного промежутка больше (точнее не меньше) объема выпускаемой продукции для краткосрочного промежутка.

Эти объемы сравняются, если издержки производства С будут такими, что х"(С) = х2" (см. рис. 11.8). Горизонтальная прямая х2 = х," называется краткосрочной линией развития производства фирмы.

ч
	\^ РХ+Р&=С"
0
Рис. 11.8

11.5. Комбинация ресурсов (факторов производства), минимизирующая издержки при фиксированном (общем) объёме выпуска

Для случая долговременного промежутка рассмотрим задачу минимизации издержек производства при фиксированном объеме у выпускаемой продукции (т.е. рассмотрим задачу 2):

р.х.+р2х=С(х.,хЛ

min

(16)

при условии, что

y=Axvx,)

(х,>0,х2>0).

(17)

Геометрически решение задачи (16), (17) аналогично решению задачи (7), (10) (см. рис. 11.9): в случае задачи (16), (17) следует перемещаться по изокостам на "юго-запад" (ибо имеем задачу минимизации) до тех пор, пока они продолжают иметь общие точки с изоквантой, соответствующей фиксированному объему у. Ясно, что решением задачи минимизации издержек будет общая точка (х^у),х2{у)) изокосты и фиксированной изокванты. Эта точка касания зависит от объема у (поэтому и написано (х®{у),х,°(у))). Если объем у изменится, то изменится и точка (х°(у),х°(у)). Множество

	\л\ /1
ф)
0	ф) х,
Рис. 11.9

точек (х]а(у),х2°(у)), соответствующих различным объемам у выпускаемой продукции, образуют линию L (см. рис. 11.9), которая, очевидно, совпадает с линией Ірис. 11.6.

Решим задачу (16), (17) формально с помощью функции Даг-ранжа

L{xvxv) = ptx, + р2х2 + Х(у -fix^x,)). Для функции Лагранжа выписываем систему уравнений

dL(xt,x2,) _о dL(xvx2,X) dL(xrx2,) =Q dx, ' дх2 ' д

или в развернутом виде

дДх.л.А) dftx.,x„X)

p=XJ ' 2 , р7=К 1 2 =0 (18)

У[ дх, И2 дх2 v '

Критическая точка (х"(у), х,°(у), Хи{у)) функции Лагранжа, удовлетворяющая системе (18) и взятая без последней координаты а(у), т.е. точка (х^у), х2°(у)), и есть решение задачи (16), (17) минимизации издержек приданном фиксированном объеме производства у. Подставив точку (х^Су),*,0^) Д0(у)) в первые два уравнения системы (18), получим два тождества. Поделив почленно первое тождество на второе, получим, очевидно, выражение (3) (множитель Х°(у) сократится, как и в случае раздела 4 множитель Ха(у)>0). Получили аналитическое обоснование того, что изокоста и изокванта касаются в точке (х'](у),х"(у)) (см. рис. 9). Характер взаимосвязи между критической точкой функции Лагранжа без последней координаты и решением задачи (16), (17) минимизации может быть прокомментирован здесь подобно тому, как это было сделано в разделе 4 для задачи максимизации.

В разделе 2 в точке локального рыночного равновесия (х",х2а) был определён объём производства y=j[x{x2). Если в ограничении (17) положить у=у0, то несложно показать, чтохДу^х,0, х,°(>>())=х20, а также °(у0)=рп, т.е. множитель Лагранжа Х°(у0) равен рыночной цене р0 единицы выпускаемой продукции. Таким образом, предложена естественная экономическая интерпретация множителя Лагранжа Х"(уа).

Подставив х^Ху) и х2Ху) в выражение С(хг х2) = рххх + р2х2, получим выражение для издержек

р1х°{у)+р2х°{у) = С(у)

как функцию объема выпускаемой продукции, а не как функцию С(х}, х2) = ptxx + р^х2 объемов затрачиваемых (используемых) ресурсов. Вьіражение С(у) = р^х^іу) + р2х2°(у) называется значением задачи (16), (17). Так построенная функция издержек С(у) соответствует случаю долговременного промежутка. Имея выражение С(у), выпишем в явном виде представление прибыли в виде функции объемов у выпускаемой продукции:

PR(y) = Риу С(у) ,

(сравните с выражением для прибыли фирмы в терминах затрачиваемых (используемых) ресурсов см. раздел 11.1). Выражение PR(y) РгУ С(у) играет важную роль в микроэкономике.

Пусть (х°(С), x2°(Q) и у = h(Q есть решение и значение задачи максимизации (7),~(11) (см. раздел 11.4).

Пусть (x^iy), х2°(у)) и С = С(у) есть решение и значение задачи минимизации (16), (17) (см. начало этого раздела 11.5).

Пусть значение С в (12) равно значению С(у) задачи минимизации (16), (17). Тогда значение задачи максимизации (7), (11) (см. раздел 11.4) будет равно у.

Наоборот, пусть значение у в (17) равно значению у = h(Q задачи максимизации (7), (11). Тогда значение задачи минимизации (16), (17) равно С.

7 О. О. Замков

*2
0	plXl+p2x2-C(y) *»
Рис. 11.10

Таким образом, наблюдается взаимная зависимость задач (7), (11) и (16), (17) (см. рис. 11.10).

Задача минимизации издержек производства при фиксированном объеме у выпускаемой продукции для случая краткосрочного промежутка, когда фиксирован объем х* второго ресурса, имеет вид (у играет роль параметра)

ptxt + ргх* = СЦ, х*) (min) (19)

при условии, что

У=Лхг х,) (х,>0).

(20)

Ограничимся наглядным геометрическим решением задачи (19), (20) (см. рис. 11.11).

Имеет место важный результат теории фирмы:

при одном том же объеме у выпускаемой продукции издержки производства для случая долговременного промежутка меньше (точнее не больше) издержек производства для случая краткосрочного промежутка. Эти издержки производства равны друг другу, если объем / производства будет таким, чтохД/) = х* (см. рис. 11.12).

*2
х°2(у)
А
0
Рис. 11.11

Рис. 11.12

Вопросы к главе 11

Сформулируйте определения исходных понятий теории оптимизации производства.

Сформулируйте основную цель функционирования фирмы.

В чем состоит принципиальное отличие (в содержательных и в формальных терминах) в постановке задачи максимизации прибыли фирмы для случаев долговременного и краткосрочного временных промежутков?

Сформулируйте определение изокосты. Дайте экономическую интерпретацию следующему геометрическому факту: фиксированная точка (vp v2) (v: > 0, v, > 0) принадлежит прямой, имеющей уравнение p{xt + р{х2 = Си.

Пусть два набора (v,, v2) и (wp w2) затрачиваемых (используемых) ресурсов таковы, что для набора (vp v2) издержки производства меньше, чем для набора (wp w2). Как расположены относительно друг друга изокосты, соответствующие наборам (vp v2), (wp w,)? Является ли обязательным одновременное выполнение двух неравенств w{ > vp w2 > v2?

Опишите взаимное расположение изокосты и изокванты, проходящих через точку (х,0, х2°) локального рыночного равновесия фирмы (случай долговременного промежутка). Дайте обоснование их взаимному расположению.

Опишите взаимное расположение изокосты и изокванты, проходящих через точку локального рыночного равновесия фирмы (случай краткосрочного промежутка).

Чему равна (предельная технологическая) норма замены одного ресурса (для определенности, первого) другим (для определенности, вторым) в точке локального рыночного равновесия в случае долговременного промежутка?

Что такое функция спроса на ресурсы (затраты)?

Что такое функция предложения выпуска?

Сформулируйте задачу максимизации объема выпускаемой продукции при ограничении затрат на приобретение ресурсов (факторов) на аналитическом языке и на геометрическом языке (в случаях долговременного и краткосрочного промежутков).

Опишите аналитическое (для случая долговременного промежутка) и геометрическое (для случаев долговременного и краткосрочного промежутков) решение задачи вопроса 11.

Сформулируйте задачу минимизации издержек производства при фиксированном объеме выпускаемой продукции на аналитическом языке и на геометрическом языке (для случаев долговременного и краткосрочного промежутков).

Опишите аналитическое (для случая долговременного промежутка) и геометрическое (для случаев долговременного и краткосрочного промежутков) решение задачи вопроса 13.

Опишите взаимосвязь между задачами вопросов 11 и 13 (в случае долговременного промежутка).

Как определяется долговременная линия расширения производства фирмы?

Как определяется краткосрочная линия расширения производства фирмы?