14.16. непрерывные случайные величины. группировка выборочных данных по интервалам значений. построение гистограммы
14.16. непрерывные случайные величины. группировка выборочных данных по интервалам значений. построение гистограммы
При больших объемах выборки, содержащей значения некоторой непрерывной случайной величины, ее элементы группируют по интервалам значений. Для этого интервал выборки, содержащий все ее значения, разбивают на к непересекающихся интервалов, длина которых для удобства расчетов чаще всего выбирается одинаковой и равной размаху выборки, деленному на желаемое число интервалов:
с г(") _ г(1)
После того, как частичные интервалы выбраны, так же, как и в "точечном" случае, определяют частоты количество элементов выборки я, попавших ву'-й интервал, причем элемент, совпадающий с верхней границей интервала относят к последующему интервалу.
Наряду с частотами подсчитываются относительные частоты, накопленные частоты и накопленные относительные частоты. Полученные результаты также записывают в виде таблицы, первая строка которой содержит границы последовательных интервалов, а вторая соответствующие им частоты (абсолютные, относительные, накопленные и накопленные относительные частоты). Как и для "точечной" выборки, для выборки, сгруппированной по интервалам по значениям накопленных частот, может быть построена выборочная функция распределения. Для наглядного представления выборки часто используют ее графическое отображение гистограмму частот и гистограмму относительных частот. Любая из этих гистограмм представляет собой кусочно-постоянную функцию, припі ші
нимающую значения или наj-m интервале упорядоченной по
возрастанию выборки. Эту функцию представляют в виде ступенчатой фигуры, состоящей из прямоугольников шириной Ах и высо9 О. О. Замков
той
Ах
Ах
, построенных на соответствующих интервалах. Пло-
щадь j-ro прямоугольника равна Ах
1_
Ах
(или <о.), а площадь всей
ступенчатой фигуры под графиком гистограммы равна объему выборки (для гистограммы частот) или единице (для гистограммы относительных частот).
В качестве примера рассмотрим гистограмму распределения по росту людей в какой-либо выборке, например студентов одного из институтов:
| Рост h | 155-16 | 160-16 | 165-17 | 170-17 | 175-18 | 180-18 | 185-19 |
| 1\%/п | 0,07 | 0,15 | 0,20 | 0,25 | 0,18 | 0,10 | 0,05 |
Высота каждого столбика в изображенной на рисунке гистограмме пропорциональна количеству людей, рост которых попадает в соответствующий интервал. Допустим, что у 250 из 1000 выбранных для обследования студентов рост находится в пределах от 170 до 175 см (170 < h < 175 ). Тогда на гистограмме высота столбика,
S ,,=0,07+0,15+0,20+0,25+0,18+0,10+0,05-1
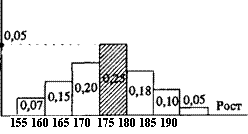 |
Относительная частота п я(ПО ^ h < 175)
соответствующего этому интервалу, равна = п
250 л,
0,05, а площадь под этим столбиком — = 0,25.
1000-5 ' ' " л
Аналогично в рассмотренном выше примере, если рассматривать рост студентов А в качестве значений случайной переменной Я, то при достаточно большом числе наблюдений относительные частоты появления значений hk в интервале A < Я< А+ДА будут стремиться к вероятности попадания значений роста в вышеуказанный интервал Prob{A < Я < h+Ah}, а относительные накопленные частоты к вероятности РгоЬ{Я< А}, которая является функцией конкретного значения А и называется функцией распределения FH(h) непрерывной случайной величины Я.
Если длину интервала ДА устремить к нулю,»то вероятность попадания в каждцй конкретный интервал также будет стремиться к нулю. Однако отношение этой вероятности к длине интервала стремится при этом к постоянной величине, называемой плотностью вероятности. Плотность вероятности можно интерпретировать как вероятность попадания реализации случайной величины Я в бесконечно малый интервал, содержащий точку А, в расчете на единицу его длины:
ДА) = ШРгоЬ^ ^ Н < h + Ah} (Q) л/,-0 Ah
График функции ДА) будет гладким (для гладких F), в отличие от графика относительной частоты попадания в единичный интервал.
Более строго, если случайная величина является непрерывной, т.е. принимает любые значения из некоторого интервала, то для нее уже нельзя определить вероятность того, что она принимает некоторое конкретное значение (точечную вероятность). Поскольку в любом конечном интервале содержится бесконечное число значений, то вероятность выпадения одного из них всегда равна нулю. Однако функция распределения случайной величины F^x), определяемая как вероятность того, что случайная величина принимает значение меньше данного числах:
Fx(x) = ?rob{X<x}, (10)
сохраняет смысл и для непрерывной случайной величины. В данном случае это некоторая непрерывная неубывающая функция действительного аргумента х.
14.17. Основные характеристики случайных величин ("статистики")
Для любой случайной величины важную роль, помимо функции распределения, играют числовые характеристики ее распределения, важнейшими из которых являются среднее значение (математическое ожидание случайной величины) и дисперсия. Среднее значение является характеристикой положения частотного распределения, а дисперсия мерой ширины или разброса распределения. Во многих практических случаях информация о случайных переменных, содержащаяся в частотном распределении является избыточной. Например, для принятия решения о покупке акций важно, в первую очередь, знать средний доход на них и риск инвестирования в них денег, характеризуемый степенью разброса среднего дохода (дисперсией), что эквивалентно знанию положения и ширины частотного распределения возможных доходов на акции.
14.17.1. Среднее значение. Математическое ожидание
Пусть имеется, например, выборка объемов продаж холодильников за 10 дней: {хк} = {1,5,5,6,2,5,6,2,6,5}. Среднее значение объема продаж за один день для этой выборки мы получим, если сложим все выборочные данные и разделим сумму на их число:
1 Л 1+5+5+6+2+5+6+2+6+5
Х = N 5**= І0 = 4Д
Если мы посмотрим на сумму в правой части равенства, то заметим, что многие числа в ней повторяются. При этом число повторений, деленное на общее число данных в выборке, является ни чем иным, как частотой появления соответствующих значений в выборке. Следовательно, среднее значение можно определить и так:
х = Ex*'w* = 1 0,1 + 20,2 + 5 0,4 + 60,3 = 4,3, (11)
м
где суммирование ведется по всем различным значениям случайной величины X, встречающимся в выборке (в данном примере {хк} = {1,2,5,6}), а в роли весов выступают частоты этих значений (причем сумма весов равна единице).
В пределе достаточно большого числа наблюдений N частоты wk значений хк переходят в соответствующие вероятности Рк = РоЬ{Х=хк}, и дискретная случайная величина X может быть представлена в виде таблицы значений {хк}, которые может принимать случайная величина, и соответствующих им вероятностей Рк -РтЫо{Х=хк):
| X | *. | Х2 | X II | |
| р | Л | р II |
Математическое ожидание или среднее (по генеральной совокупности) значение такой случайной величины определяется как взвешенная сумма всех возможных реализаций случайной величины X, в роли весов в которой выступают вероятности этих реализаций, причем сумма весов равна единице:
МХ = х, 7>, + х2Р2 + ... + х />„ = Е Pk-*k. (12)
Это числовая характеристика (а не функция, на что указывают квадратные скобки) случайной величины X, что означает, что она соответствует всей величине X, а не различным конкретным ее значениям. Другие обозначения среднего значения: ЩХ = <Х> = тх = и.
Математическое ожидание непрерывной случайной величины определяется следующим образом:
♦ OD 4 00
МХ = xdFx(x) = ^xfx(x)dx (13)
Свойства математического ожидания:
Мс = с;
МХ+Ь = МХ + Ь;
МаХ = аМХ\;
MaX+b = аМХ] + Ь,
для любых чисел (констант) а, Ь и с.
Эти свойства вытекают из определения математического ожидания. Если Хн Yслучайные величины, то можно определить новые
f х
случайные величины (Х+ К), (ХУ), (XY), -р , рассчитав вероятности
принятия ими конкретных значений (х+у), (х-у), (ху) и
Для любых случайных величин Xw Y
MX+Y = МХ + MY.
(14)
Математическое ожидание (ожидаемое, или среднее, значение) часто рассчитывается при сравнении затрат и выгод действия со случайным исходом, например ожидаемого выигрыша в лотерее или ожидаемого дохода на акции или другие рисковые ценные бумаги.
Выборка может рассматриваться как дискретная случайная величина, принимающая значения xrxv...,xn с вероятностями '/я (если некоторые значения х. совпадают, то для расчета выборочного среднего и других характеристик они могут условно рассматриваться как разные, что не меняет результата), то естьрк~у/пдля всех 1 <к<п. Обозначая выборочное среднее как тп, имеем
тИ1хвх = ±£хк. (15)
Нижний индекс п показывает объем выборки, для которой вычисляются выборочные характеристики.
Для разных конкретных выборок, соответствующих одной и той же генеральной совокупности, выборочные средние будут, вообще говоря, различны.
14.17.2. Дисперсия
Когда мы имеем дело со случайной величиной, то, как правило, недостаточно определить только ее среднее значение, но и следует ввести меру ее разброса вокруг среднего значения, характеризующую вариативность значений случайной величины. Так, например, для выборки объемов продаж холодильников важно знать не только средний объем продаж, но и то, в каких пределах он может изменяться ото дня ко дню.
Одной из мер вариативности является дисперсия, определяемая как средний квадрат отклонения случайной величины от среднего значения. Для ее определения мы находим отклонения объемов продаж в каждый из дней от среднего значения, возводим их в квадрат и усредняем (складывая и деля на число наблюдений, уменьшенное на единицу):
Используя определение частот появления различных значений в выборке, мы, так же как и в случае среднего значения, можем переписать формулу для расчета дисперсии в виде
Djxi-^gh -і»"". -™ -3,5,
В пределе достаточно большого числа наблюдений п частоты со4 значений хк переходят в соответствующие вероятности Рк = РгоЬ{Л=дгА}, и для анализа отклонений случайной величины от среднего значения полезно ввести в рассмотрение новую случайную величину Z = (X ц)\% значения которой представляют квадраты отклонений случайной величины Л"от среднего значения х = ЩХ. Распределение этой случайной величины также можно представить в виде таблицы:
| Z | (*, м)2 | (*2 ц)2 | ( ц): | |
| р | Л | Рп |
Математическое ожидание такой случайной величины
ВД = г,7> + *,7>, + ... + Z„-P„ = (16) = Е*Л " 1>*'Л = ^(X-A/IJI)-1!.
характеризует среднее отклонение (точнее, средний квадрат отклонения) исходной случайной величины Хот среднего значения М[Х] = ц и называется дисперсией случайной величины X, обозначаемой D(X) или а2.
Итак, общее определение дисперсии как для дискретной, так и для непрерывной случайной величины имеет вид
DX = М\{Х МХ)(17)
Свойства дисперсии:
Dc = 0;
DX+b = DX\:
DaX] = a-DX\:
DaX+b = a-DX
для любых чисел (констант) a, b и с.
Эти свойства могут быть доказаны из определения дисперсии и свойств математического ожидания.
14.17.3. Связь дисперсии с математическим ожиданием
Для практического расчета дисперсии случайных величин часто бывает удобно использовать следующую формулу:
DX = МХ (МХ)
(18)
Эта формула легко выводится из определения и свойств дисперсии. Раскрывая квадрат разности в (18) и пользуясь свойствами математического ожидания, имеем:
DX = М(ХМХ)= М\{Х 2МХХ+ (М[ХУ = = МХ2МХ МХ + (МХУ = МГ(М[ХУ.
Стандартное отклонение случайной величины о мера разброса случайной величины вокруг среднего значения, имеющая размерность данной случайной величины. Если случайная величина .v измеряется в $, то величина а измеряет ее разброс вокруг среднего также в $. Стандартное отклонение это среднее квадратическое разброса случайной величины, или квадратный корень из ее дисперсии:
оХ = ЩЩ (19)
Коэффициент вариации случайной величины Vмера относительного разброса случайной величины (безразмерная величина).
|. и*! = Ж (20)
11 М[Х]Коэффициент вариации показывает, какую долю среднего значения случайной величины составляет ее средний разброс.
Дисперсия и другие меры разброса часто применяются при анализе риска различных активов в портфеле и портфеля активов в целом в финансовом анализе, а также при анализе риска других действий со случайным исходом.
Пример расчета числовых характеристик дискретной случайной величины: случайная величина Х количество "решек", выпавших
Для нее ЩХ
при бросании монеты, распределена по закону
О 1
= ОУг+1 У2=У2; DX = МіГ-І-МІХ]2 = (02V2+12V2)-(V2)2=V4; о <JD[X] = {чГ = Уг; У[Х] = Уг:У2=1.
Обсуждение Математические методы в экономике
Комментарии, рецензии и отзывы
