17.5. модель инфляции. эконометрическая оценка nairu
17.5. модель инфляции. эконометрическая оценка nairu
В заключение главы рассмотрим еще один пример использования модели множественной линейной рефессии в макроэкономическом анализе. Предположим, что у нас есть ряды статистических данных уровней инфляции и безработицы в экономике США за 1977-1990 гг., и что мы хотим оценить взаимосвязь между этими показателями. Из теоретических соображений мы можем предполагать, что темп инфляции отрицательно связан с уровнем безработицы и, кроме того, обладает определенной инерцией. Мы также предполагаем, что существует некоторый "естественный" уровень безработицы, не воздействующий на темп инфляции. Этот уровень называется NAIRU Not Accelerating Inflation Rate of Unemployment ("уровень безработицы, не ускоряющий инфляцию"). Предположим в соответствии со сказанным, что формула зависимости этих показателей имеет вид
INF = а (и и) + b INF(-),
(9)
где INFтемп инфляции, INF(-) темп инфляции предыдущего года (инерционная составляющая, описывающая ожидаемую инфляцию), и уровень безработицы, и NAIRU, а и b неизвестные коэффициенты. Для указанных временных рядов было оценено следующее уравнение множественной линейной регрессии:
INF = 5,414 0,920-м + 1,148 INF(-) (10)
(0,930) (0,154) (0,086) R2 = 0,942; DW= 2,07.
В скобках указаны стандартные ошибки соответствующих коэффициентов. Можно отметить, что статистическое качество полученного уравнения регрессии практически идеально. Все г-статистики превышают 5 по абсолютной величине (а, грубо говоря, границей для очень хорошей оценки является 3). Очень высока доля дисперсии зависимой переменной, объясненная с помощью уравнения регрессии, 94,2\% особенно с учетом того, что уравнение регрессии связывает относительные величины, не имеющие выраженного временного тренда. Статистика Дарбина-Уотсона Dкочень близка к 2, и, даже не прибегая к таблицам, здесь ясно, что гипотеза об отсутствии автокорреляции остатков первого порядка будет принята при любом разумно малом уровне значимости. Итак, мы имеем хороший пример линейной регрессии, когда можно оценить ее статистическую значимость, не прибегая к таблицам распределений Стьюдента, Фишера или Дарбина-Уотсона, а лишь по общему порядку полученных статистик.
Теперь рассмотрим содержательный смысл и теоретическую интерпретацию полученного уравнения. Оно показывает, что инфляция является очень инерционным процессом, и то, что коэффициент 6=1,148 превышает единицу, говорит о том, что это процесс самоускоряющийся. Последнее существенно усложняет задачу контролирования и сдерживания инфляции. Учитывая,что в соответствии с нашей моделью, 5,414 0,920 и = а(и и), получаем а = 0,920 и и ~ 5,414/0,920 = 5,885 (\%). Итак, если мы принимаем исходную общую формулу модели инфляции, то мы тем самым получаем из нее оценку естественного уровня безработицы (NAIRU) для экономики США в 1977 1990 гг. Она оказалась несколько меньшей, чем 6\%, что согласуется с другими оценками, полученными различными методами.
ПРИЛОЖЕНИЕ ^-распределение Фишера
Это распределение (называемое иногда распределением дисперсионного отношения) имеет случайная величина, равная отношех2(*,)
нию двух независимых случайных величин: величины —г—, вырак
жающейся через случайную величину, имеющую распределение х2 с
к1 степенями свободы и величины —г—, выражающейся через случайную величину, имеющую распределение х2 с к2 степенями свободы.
Х2(*,) х1(кг)
Вводя новую случайную величину Д/с.,/с,) = —г— : —г—, мы
к, к2
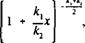
получим для нее распределение Фишера ск^и к2 степенями свободы с плотностью вероятности:
*,
/р,к,,к2) = Сх1 V
М[Х = j-^ (А:2>2), D(X)=h(kvk2).
При больших kt и к2 это распределение приближается к нормальному.
| 1,0 | ||
| *i=l;*2=5 | ||
| j Jfei=10;Jfe2=10 | ||
| 0,5 | ||
| 0 | 1 2 3 | 4 * |
Критические точки распределения Фишера обладают следующим свойством:
_ 1 FSkvki) FJfcj,*,) • Квадрат случайной величины, имеющей распределение Стьюдента с к2 степенями свободы имеет распределение Фишера с (1 ,к2) степенями свободы.
Подставляя в определение случайной величины /•'"выборочное
г v 1ч (n-l)S„"2
представление случайной величины х • X (п ~ ') = >
о2
 можно получить "выборочное представление" случайной величины Р.
можно получить "выборочное представление" случайной величины Р.
где S"2 = —^—rSn2 ~ гЕ^* " исправленная выбороч" л 1 п ная дисперсия для выборки объема п.
Распределение Фишера используется, например, при:
сравнении двух дисперсий;
проверке гипотезы об одновременном равенстве нулю всех или части коэффициентов линейной регрессии;
проверке гипотезы о совпадении всех коэффициентов двух уравнений линейной регрессии.
Работа с таблицами /^-распределения Фишера
Таблицы функции /^-распределения Фишера на интервале [0,+оо) обычно приводятся отдельно для различных значений вероятности а попадания в "хвост" функции распределения. Например, для а = 0,05 такая таблица имеет вид
| k2 kl | 1 | 10 | 100 | 00 | ||
| 1 | 161 | 242 | 253 | 254 | ||
| 10 | 4,96 | 2,97 | 2,59 | 2,54 | ||
| 100 | 3,94 | 1,92 | 1,39 | 1,28 | ||
| 00 | 3,84 | 1,83 | 1,24 | 1,00 |
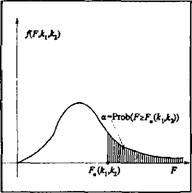
В этой таблице для различных сочетаний чисел степеней свободы кх и к2 приведены критические точки функции распределения Фишера, соответствующие вероятности а = 0,05 попадания в "хвост" функции распределения.
Критическая точка Fa(kvk2), например, F005(10, 100), находится в таблице, соответствующей значению а = 0,05, на пересечении строки к2 (в данном случае к2 = 100) и столбца (в данном случае кх = 10). Из приведенной таблицы находим, что F0iOS(10, 100) = 1,92. Напомним, что критическая точка в данном случае имеет следующий смысл: Prob{/r> Fa(krk2)} — а.
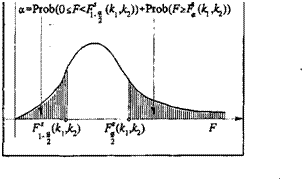
Отметим, что иногда таблицы /•'-распределения приводятся для двусторонних критических точек F^(kvk2), определяемых из условия
?xob{Fx_J(ks,k2) F< Fa/>(kx,k2)} = 1 а.
Появление здесь величины а/2 объясняется тем, что при заданной вероятности а попадания в оба "хвоста" функции распределения вероятность попадания в каждый из "хвостов" функции распределения обычно считается одинаковой. Следовательно, она в два раза меньше а и равна а/2.
 |
Вопросы к главе 17
Из каких этапов состоит проверка качества оцененного уравнения регрессии?
Как рассчитывается и что показывает коэффициент детерминации R2?
Коэффициент детерминации R2 = 0,5. Что можно сказать о качестве оцененной формулы в целом? Какая нужна дополнительная информация?
Что такое распределение Фишера? В каких задачах эконометрики оно используется?
Если нулевая гипотеза для статистики Фишера отвергается, то что можно сказать про оцененную парную линейную регрессию?
Таблицы каких распределений используются при оценке качества линейной регрессии?
Какие показатели характеризуют независимость отклонений зависимой переменной от линии регрессии? Как осуществляется проверка этой независимости?
В каких случаях наблюдается положительная автокорреляция отклонений е.? Приведите примеры из экономики.
Статистика Дарбина-Уотсона оказалась близкой к четырем. Что это означает?
Если у зависит от х как квадратичная функция у = х2, но оценена связывающая их линейная регрессия, то какой окажется величина DW]
Как осуществляется прогнозирование экономических показателей с использованием моделей линейной регрессии?
Как можно оценить "естественный" уровень безработицы с использованием модели линейной регрессии?
Обсуждение Математические методы в экономике
Комментарии, рецензии и отзывы
