2.4. динамическая модель межотраслевого баланса

2.4. динамическая модель межотраслевого баланса

Статический межотраслевой баланс описывается системой уравнений (2.7), в которой в каждом уравнении выпускаемая отраслью валовая продукция приравнивается сумме продукции, поглощаемой этой отраслью и всеми другими отраслями, и чистому выпуску, т.е. продукции конечного использования. Если теперь матрицу продукции конечного использования в каждый год Xу ' представить как сумму инвестиций Z(tj = B(tj(X(tj-X(t и продукции конечного

потребления Y(t1, то динамическая модель будет выглядеть следующим образом:

X (t1 = AX (t1 + B(t1 (X (t1 X (t-11 ) + Y (tj, (2.14) где индекс t в скобках сверху у буквы означает номер года, матрица B характеризует инвестиции, поставляемые из отрасли в отрасль и вводится аналогично матрице прямых материальных затрат A . Элементы матрицы А определяются по первой формуле (2.4).

Аналогичным образом определяются элементы матрицы j, т.е.

(t 1

bij j= ігуану, (2.15) xj xj

где zij — элемент матрицы B ' поставки продукции отраслью і на

и

инвестиционные цели в отрасль j.

В динамической модели межотраслевого баланса рассматриваются показатели модели для концов периодов под номером t , изменяющихся от 1 до т . В качестве начальных условий задается вышуск в нулевом году X(0). При известном конечном шотреблении Y(t) уравнение (2.14) можно шредставить в виде:

(е A(t)B ('))' X (') = Y (')B (')' X (t-1)

Решение этого уравнения

X(t) = ( е A(t)B(t '(Y(t)B(t)' X. (2.16)

Как следует из этой формулы, для увеличения вышуска X(t) надо увеличивать конечное шотребление Y(t) шо сравнению с предьI-дущим годом.

Представим шроизведение двух матриц B(t)(X(t)-X(tв виде

матрицы-столбца инвестиций Z(t)= B(t)(X(t)-X(t-1)). Тогда шри известном вышуске и конечном шотреблении формулу для этой матрицы-столбца можно найти из уравнения (2.14). Эта формула имеет вид:

Z(t )=(е A)X(t)Y(t).

В модели межотраслевого баланса реальной экономики обязательно действуют ограничивающие факторы. Одним из таких факторов является ограничение на трудовые ресурсы, задаваемые неравенством

l' х(t )< L(t),

где L ' — трудовые ресурсы; l — матрица-строка трудоемкости, или затраты труда на шроизводство единицы шродукции.

При учете отраслевых мощностей необходимо учитывать, что валовой вышуск ограничен этими мощностями. Это ограничение задается шри шомощи естественного неравенства

х(t )< х(tz (t),

где х(t) — матрица-столбец отраслевых мощностей.

Если ввести коэффициент выбытия мощностей ці i-й отрасли, то отраслевые мощности этой отрасли могут быть заданы равенством

х(t ) = (1 )х(tz(t).

Рассмотренная здесь динамическая модель межотраслевого баланса предполагает, что в рассматриваемом периоде мощности отраслей используются полностью. Поэтому в периоды кризисов или в условиях переходной экономики вместо равенства (2.14) следует использовать систему неравенств, показывающих, например, что общий валовой выпуск должен покрывать текущие производственные затраты, затраты продукции на расширение производственных мощностей и на непроизводственное потребление. Валовые выпуски отраслей не должны превышать производственные мощности и имеющиеся трудовые ресурсы.

> Пример 2.3. Для примера, приведенного в табл. 1.4, данные которой принимаются в качестве начальных условий задачи, рассчитать параметры межотраслевого баланса для первого и второго годов. При этом непроизводственное потребление принять:

(1)-Г1101 - в„ 2: V (1)-Г1201 V (2)_Г1301

вариант 1: V -II; вариант 2: V ||, V

[150J [160J [170 ,

Матрицу B(t), характеризующую инвестиции, поставляемые из отрасли в отрасль, принять независимой от времени и равной:

0,06 0,02 0,04 0,1

Решение. Как следует из данных табл. 1.4, общий валовой выпуск в год под номером ноль определяется матрицей(0) (2001 столбцом х- ||.

Элементы матрицы прямых материальных затрат а определяютХ 50

ся по первой формуле (2.4). Например, a11 _ _ 0,25,

x1 200

a,, _Х-12_-40_ 0,16 и т.д. Таким образом, матрица прямых 11 x2 250

материальных затрат имеет вид:

'0,25 0,16

0,35 0,12

Вариант 1. Выпуск в первом году находим по формуле (2.14). Подставив в (2.14) исходные данные, получим

X

(і).

1-0,25-0,06 -0,16-0,02 -0,35 0,04 1 0,12 0,1

-1 с

110 150

0,06 0,02^

0,04 0,1 J 250j

0,69 -0,18 -0,39 0,78

-ч

Г110^ Г17

^150) у 33

0,69 -0,18 0,39 0,78

( 93 1117

(200Л Л250)

Выпуск в первом году равен выпуску нулевого года. Полученного результата следовало ожидать, так как в табл. 1.4 приведен баланс без учета инвестиций. Этот результат легко проверить, подставив полученные данные в формулу

Y (1)

Z (1)=(Е A)XY

Л1)

'1 0,25 -0,16 Л(200^ Г110 ^ _ Г110 ^ Г110 Л_( 0 У-0,35 1 -0,12Д250) ^150Д^150) ^150)_{0

Очевидно, что для второго года получим тот же результат.

(1).

Y

1160

Вариант 2. В этом варианте, в отличие от предыдущего, непроизводственное потребление определяется матрицей-столбцом Г120 Л

. Тогда выпуск в первом году будет равен:

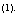X

-ч

120 160

17 V

33 J

1 -0,25-0,06 -0,16-0,02 . -0,35-0,04 1 -0,12-0,1

0,69 -0,18 -0,39 0,78

Л Г Г120 ^ Г0,06 0,02^1 f200^ ^ ' ^160) [0,04 0,1 J250J, ~

0,69 -0,18Г103220,51^ -0,39 0,78) ^127 Д[273,08,

Матрица-столбец инвестиций будет равна

(1)

1 -0,25 -0,18 V220,51^ Г120^| Г 121,69^ Г120^|

0,35 1 0,12 )У273,08) у 160 ) у 163,13 ) ^160 )

1,69 ^

3,13))

Элемент матрицы B поставки продукции z),' отраслью i на

и

инвестиционные цели в отрасль j находят из соотношения (2.15). Этот элемент находят по формуле

ij

XX(

Предварительно найдем разность между матрицей-столбцом выпуска в первом году и в нулевом году:

( 220,5f| (200А = ( 20,5f|

273,08) [250) = {23,08)'

Используя эти данные, получим

7« 11

21

7 «■

г (X2) X2))=

(X(1)X(0))-21 1 1 0,06 • 20,51 = 1,23; = 0,02 • 23,08 = 0,46; = 0,04 • 20,51 = 0,82; = 0,1-23,08 = 2,31.

Проведем проверку, подставив результаты в правую часть ис-

ходной формулы X

(1)

,AX B XX (0)) + Y

0,25 0,16А (220,5f| (0,06 0,02А (20,5ГА (120А 0,35 0,12)273,08) + ^0,04 0,1 J23,08J + ^160)'

98,82 А (1,69А (120А_(220,51 109,95 J +I 3,13 J +1160 J _ I 273,08

После проведения расчетов получим результат, тождественно равный валовому выпуску за первый год.

За второй год непроизводственное потребление определяется

(2) (130А

матрицей-столбцом Y ' = I J. Тогда выпуск во втором году будет равен:

^170) ^0,04 0,1 ) ^273,08)

0,69 -0,18А-1 (111,31 А=(237,00А 0,39 0,78)J II133,87)J=II290,13

г1-0,25-0,06 -0,16-0,02^-1 ((130А (0,06 0,02А (220,51^

0,69 -0, 27 -0,39 0,78

-0,35 -0,04 1 -0,12 -0,1 J

^170 ) ^ 36,13 )

-1 ((130А(18,69АА

Матрица-столбец инвестиций будет равна:

(2)_Г1" 0,25 -0,18 Л f237,00Л f 130 Л _ ^ 131,34 Л f^_f 1,34 _[-0,35 1 0,12 Д290,13 ) ІД70 J_^172,36) ІД70 )_{ 2,36

Элемент матрицы B поставки продукции zij) отраслью i на

и

инвестиционные цели в отрасль j находят из соотношения (2.15). Этот элемент находят по формуле

X(2)X

Предварительно найдем разность между матрицей-столбцом выпуска во втором году и в первом году:

f237,00Л f220,51Л _ f 16,49Л

(-12)x(1)) = b12 (-22) --21)) _ 0,02• 17,05 _ 0,341; b21 (-12) - _ 0,04 -16,49 _ 0,66;

' [ 290,13 ) [273,08) _ ІД7,05J'

Используя эти данные, получим

, (2)

z 2)

12

z 2)

z1{> _ b111 x1 ' x1>) _ 0,06 • 16,49 _ 0,99:

z22) _ b221 xV x4 I _ 0,1 • 17,05 _ 1,705'

Проведем проверку, подставив результаты в правую часть исходной формулы X(2) _ AX(2)+ B(X2 -X+ Y(2):

f0,25 0,16Л f237,00Л f0,06 0,02Л f 16,49Л f 130 [0,35 0,12Д290,13) + ^0,04 0,1 Д 17,05J + ^170

_f105,67Л f 1,33 Л f 130 Л_f237,00 _ ^117,77) + [2,36ДІД70J Д290,13

После проведения расчетов получим результат, тождественно равный валовому выпуску за второй год. ◄ 2.5. Модель Неймана

Модель Неймана [1, 4—6] применяется для изучения расширяющейся экономики. Эта модель, в отличие от модели Леонтьева, допускает производство одного продукта различными способами. Количество выпускаемых продуктов будем обозначать буквой n (в модели Леонтьева этой буквой обозначали количество отраслей), а количество способов их производства — буквой т. Количество отраслей в модели Неймана не рассматривается. Каждый способ производства под номером j задается матрицей-столбцом затрат

J2 j

на единицу интенсивности и соответствующей матри-

V \%nj J

цей-столбцом выпусков

( b1 j Ї

Ь2 j

. Таким образом, в результате

V bnj J

производственного процесса затрачивается матрица-столбец

выпускается за счет этого матрица-столбец bj.

Интенсивностью производственного процесса называется объем товаров или услуг, выпускаемых в результате этого процесса в единицу времени.

Пара [cij, bj j характеризует технологический потенциал, заложенный в процессе под номером j , и называется базисом этого j-го производственного процесса. Все базисы производства называются базисными процессами. Базисные процессы можно описать матрицей затрат A и матрицей выпуска B .

(Хлл(Хл '

B

(bll b12 b21 b22

Vbnlbn2

Коэффициенты затрат и выпуска неотрицательны, т.е. atj > 0 и bj > 0. Поскольку для реализации любого процесса необходимы затраты хотя бы одного продукта, то для каждого j найдется хотя бы одно i , для которого

aj > о.

Аналогично, так как каждый продукт может быть произведен хотя бы одним способом, для каждого i найдется такое j , что

bj > 0.

Продукция, идущая на конечное использование, в явном виде в модели Неймана не выделяется. Так как все секторы в модели рассматриваются как внутренние, или эндогенные, то рассматриваемая модель является замкнутой.

В модели Неймана заложен динамический процесс, причем осуществление затрат и выпуска готовой продукции разделено вре-меншім интервалом, например годом. Номер года будем обозначать буквой t. Тогда t = 0,1,..., T, где T — общая длительность всего

производственного процесса. Номер года помещается в виде верхнего индекса при показателе в скобках. Если матрицу-столбец ин-тенсивностей производственных процессов обозначить

X

то матрицу-столбец затрат и матрицу-столбец выпусков для года под номером t соответственно можно представить в виде

AX(t) и BX(t).

и

Одним из условий модели Неймана является требование использования для производства товаров и услуг в данном периоде только тех продуктов, которые были произведены в предыдущем периоде. Отсюда следует, что затраты AX(t) в периоде под номером t не должны превышать выпуска в периоде под номером t -1. Поэтому должны выполняться условия

AX(t) < BX(t-1), (2.17) где t = 0,1,..., T — номер периода; Bx^° — начальные условия, или матрица-столбец запаса товаров к началу процесса.

Модель Неймана, представленная в виде (2.17), задана в натуральной форме.

Матрицу-строку цен товаров можно ввести по формуле

ру ! = (pi p2!... Pn'),

где pf) — цена продукта под номером i в году под номером t, pf) > 0 .

Тогда издержки по всем базисным процессам в период времени

t можно записать в виде матрицы-строки P(t-\^A (затраты осуществляются по цене начала периода), а выручку в период времени

t — в виде матрицы-строки P(B (готовая продукция оценивается в конце периода). Модель Неймана в денежным выражении представляется в виде

P(t-)A > P(t)B , (2.18)

P(t-)AX(t) > P(t)BX(t), (2.19) где t = 0, ,T — номер периода.

Из выражений (2.18) и (2.19) следует, что ни один процесс в модели Неймана не приносит дохода. Одним из объяснений этого является то, что издержки относятся к началу периода, а выручка — к его концу, т.е. разнесены во времени. Если же цены во времени

падают, т.е. p(t> p(t), то существование соотношения (2.18) вполне логично, так как предприниматель может за те же деньги купить больше товаров в натуральной форме.

Если принять, что общая масса денег постоянна, то соотношение (2.19) можно записать в виде равенства

P(t-)AX(t) = P(t )BX(t). (2.20) ( 2 4 ^

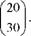
\> Пример 2.4. Дана матрица затрат A = ^i,], начальная матрица-строка цен P (0)A = (5 6 ) и матрица-столбец начальных запасов B

Найти такую интенсивность производственных процессов, при которых выпуск в конце первого года будет максимальным, и определить этот выпуск.

Решение. Используя соотношение (2.17) и условия задачи, найдем

AX

(і).

2 4

6 3 ( (і)

x(1)

2

(1)

2xj(1)+ 4x:

x( )

^ 6 Xi + 3 X2 ,

.on

2x,(1)+ 4x

v 6 x|1)+ 3x(1)y

20 ^

.30,

Выпуск в конце первого периода определяется соотношением (2.20) и будет равен:

(1WP(0)AX (1)

=(5 6).

x(1)

5x1(1)+6x2(1).

Полученные данные позволяют записать следующую задачу линейного математического программирования:

5x1(1) + 6x21) -— max

при условиях

2x,(1)+ 4x2''' < 20.

6x1(1)+ 3x(1)< 30,

x(1)> 0,

x21)> 0.

Методы решения таких задач изложены во многих книгах, например, в [2, 3]. Рассматриваемую задачу можно решить графическим способом. Построим область решений специальных ограничений задачи. Границей первой полуплоскости является

J1)

прямая 2x1(1)+ 4x21

2x21) +10 . Эта прямая про20 или x1

ходит через две точки с координатами (10; 5) (рис. 2.1). Аналогично строим график прямой 6x1(1) + 3x21) 30 . Координатами точки пересечения являются решения системы уравнений

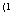2x1(1)+4x2

20,

6x1(1)+ 3x(1):

О (1) 10

Отсюда находим x — :

x(1)

10

3

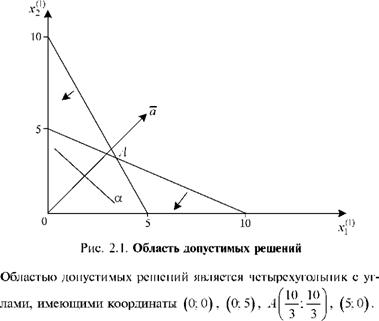
Вектор a имеет проекцию на ось 0х(1), равную 5, а на ось 0x^1) — равную 6, т.е.

a = 5 ■ i + 6 • j.

Строим вектор a и проводим линии уровня а = 5 ■ х(1) + 6 ■ x^1), перпендикулярные этому вектору.

Последней точкой встречи прямой уровня с областью допустимых

/10 10 ^ ^ (і) 10

решений является точка аI —; — J. Поэтому х1 'опт max = —;

х21)опт max =10 . Максимальный выпуск в конце первого периода будет равен

(P(1)BX= 5х«+ 6х21) = 50 + 20 = 110 ден.ед. ◄

V ' max 3 3

В общем случае динамическую модель Неймана можно записать в виде:

AX(t)< BX(t

P(t)AX(t) P(t)BX(t-1)

P(t-1)A > P(t)B,

P(t-1)AX(t)P(t)BX(t),

X(t) > 0, P(t) > 0, t 1,T.

(2.20)

Если год от года выпуск увеличивается, то говорят о сбалансированном росте производства. При этом для всех производственных процессов должно выполняться соотношение

x(t)x(t-1)+^(t-1), (2.21) где X> 0 — темп сбалансированного роста производства, t -1,T ,

Из соотношения (2.21) найдем формулу для темпа сбалансированного роста:

x(t)x(t-1)

X^-J j—

x t-1)

Если известна интенсивность к началу рассматриваемого процесса xjj0^, то соотношение (2.21) можно переписать в виде:

x(; +x)tx(°).

В этой формуле t в коэффициенте (1 + X)t является показателем степени.

Последовательность X|x(t), t-0,1,...,Tj называется траекторией производства. Если выполняется соотношение (2.21), т.е. имеет место сбалансированное производство, то траектория производства называется стационарной.

Если год от года цены уменьшаются, то говорят о сбалансированном снижении цен. При этом для всех цен должно выполняться соотношение

р(t-1)p(t)+ rpj), (2.22)

где r > 0 — норма процента, или ставка наращения, t 1,T , j -да .

Из соотношения (2.22) найдем формулу для нормы процента и цены продукта в год под номером t :

(t-) (t) pj 'pj (t) (t-)

pp ' + r '

Если известна цена к началу рассматриваемого процесса pj0 , то соотношение (2.22) можно переписать в виде:

(00) (л , V (t) (t) (0)

( + r)

В рассматриваемом случае последовательность p = ^p(t t = 0,,..., T|

называется стационарной траекторией цен.

Если для модели Неймана существуют стационарная траектория

производства X = ^ X(t t = 0,,..., T |, стационарная траектория цен

р = >^р( t = 0,1,..., T |, темп сбалансированного роста производства

1> 0 и норма процента r > 0 , то указанные четыре показателя в комплексе образуют состояние динамического равновесия в модели Неймана.

Среди всех темпов сбалансированного роста производства 1 и норм процента r можно выбрать максимальный темп сбалансированного роста производства и минимальную норму процента. Обозначим максимальный темп сбалансированного роста производства как 1, а минимальную норму процента — r . В [1] показано, что в состоянии равновесия 1 и r существуют и равны между собой:

1 = r =—г-, 7т,

P(t)AX(t)

если для начальных условий выполняется соотношение

_ = _ = р(0)bx(0) = r = P(0)AX(0)~ .

Для условий максимального темпа сбалансированного роста производства и минимальной нормы процента траектория производства

X = { X(t t = 0,1,..., T j

называется траекторией равновесного роста, или траекторией Неймана, или лучом Неймана, или магистралью. Эта траектория соответствует максимальному сбалансированному росту:

х(t )=(i +_)tx(0>

( 0,8 4Л

> Пример 2.5. Для модели Неймана с матрицами A ■

B = I 24 I и с начальными условиями Р ' = (24 30) , X I 40 I

найти максимальный темп сбалансированного роста производства и минимальную норму процента, а также луч Неймана. Решение. Максимальный темп сбалансированного роста производства и минимальную норму процента определим по формуле

_ _ p(\%х(°) 1 (24 зо)(1 3I4Q

= _ = P(0)AX(0)~1 ~,„, „j0,84Y50

3 И 40

(24 30)1 1

(24-1 + 30 ■ 2)50 + (24 ■ 3 + 30 ■ 4 )40

= — - і 1 1 = 0 2

(24 ■ 0,8 + 30-1)50 + (24 ■ 4 + 30 ■ 3)40

Для первого периода получим

Х(1)= x(0)+_x(0); _ = 0,2; x1(1)= 50 + 0,2 ■ 50 = 60; x21") = x20)+_x20); _ = 0,2; x20) = 40 + 0,2 ■ 40 = 48;

р(1)= _ = 0,2; p1^-24= 20;

1 1 + _ 1 1 + 0,2

р21)= _ = 0,2; p1^ — = 25;

1 + _ 1 + 0,2

т p(1)bx(1) ,

p(1)Ax(1)

(20 25)

13 If 60

2 4 Jl 48

3 Jl 48

, J0,8 4 If 60 (20 25)I 1

(20+25■2 20■3+25■4)

1=0,2

(20 ■ 0,8 + 25 20 ■ 4 + 25 ■ 3)

Как и следовало ожидать, значения для нулевого и первого периодов совпали.

Луч Неймана, или магистраль, соответствующая максимальному сбалансированному росту, определяется соотношением

X(t ) = (1+Г) ■ X (0) = 1,2t

Упражнения

Задача 2.1. Найти собственные числа и собственные векторы матрицы

а

32 14

Задача 2.2. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат, матрица коэффициентов вложений, вектор валовой продукции в предыдущий период и вектор объемов чистого продукта конечного использования:

f0,3 0,1 0,4^ 0,2 0,5 0,0 0,3 0,1 0,2

; в

f0,06 0,02 0,08^ 0,04 0,1 0,0 0,06 0,02 0,08

f775,5102^ 510,2041 729,5918

f300^ 200 400

Найти валовую продукцию отраслей, прирост валовой продукции каждой отрасли и поставки продукции фондообразующих отраслей i на инвестиционные цели отраслей j:

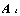(E A В )X(t) = Y

-kX

(t-1)

Г 2 2 ї

Задача 2.3. Для модели Неймана с матрицами A -I 4 ц^^1І,

B -1 3 4 J и с начальными условиями Р ' (216 162), X ' -1 I

найти максимальный темп сбалансированного роста производства и минимальную норму процента, а также луч Неймана.

Данилов Н.Н. Курс математической экономики. М.: Высшая школа, 2006.

Кузнецов Б.Т. Математика. М.: ЮНИТИ-ДАНА, 2004.

Кузнецов Б.Т. Математические методы и модели исследования операций. М.: ЮНИТИ-ДАНА, 2005.

Колемаев В.А. Математическая экономика. М.: ЮНИТИ-ДАНА,

2005.

Малыхин В.И. Математическое моделирование экономики. М.: УРАО, 1998.

Орлова И.В. Экономико-математическое моделирование. М.: Вузовский учебник; ВЗФЭИ, 2007.

Леонтьев В. Межотраслевая экономика. М.: Экономика, 1997.

Система национальных счетов / Под ред. Ю.Н. Иванова. М.: Фин-статинформ, 1996.

Федосеев В.В., Эриашвили Н.Д. Экономико-математические методы и модели в маркетинге. М.: ЮНИТИ-ДАНА, 2001.

Экономико-математические методы и модели / Под ред. А.В. Кузнецова. Минск: БГЭУ, 1999.

Экономическая теория / Под ред. В.И. Видяпина и др. М.: ИНФРА-М,

2000.

Библиографический список