4.13. предел функции при х -» °°

4.13. предел функции при х -» °°

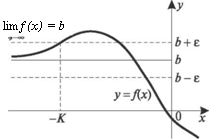
Пусть дана функция у = /(х) одной переменной х. Число Ъ называют пределом функции /(х) при х -» оо, если для любого числа є > 0 можно указать такое число К> О, что для всех |х| > ^выполняется неравенство |/(х) Ь < є (рис. 4.1).

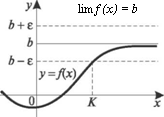О Примеры.

4 (ЛХ

1. lim = 4, так как —> 0 при х -> -н»;

*-*-! +0/2)* UJ

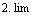lim

*^—1 + (1/2):

1 +

v *у

= 0, так как

v2y

= е (см. п. 3.12). •

—> -Н>оПрИХ^-оо.

119

4.14. Односторонние пределы

Пусть функция у fix) определена при х < х0, где х0 — предельная точка области определения функции (см. п. 3.5).

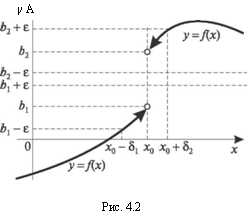
Число by f(xQ 0) называют пределом слева функции /(х) при х —> xQ, если для любого числа є > 0 можно указать такое положительное число dv что для всех х Ф х0, удовлетворяющих условию х0 -х < by, выполняется неравенство |/(х) Ьу < є (рис. 4.2):

Дх0-0) = lim /(х).

Пусть функция у=/(х) определена при х > х0, где х0 — предельная точка области определения функции.

Число Ь2=/(х0 + 0) называют пределом справа функции fix) при х -> х0, если для любого числа є > 0 можно указать такое положительное число 52, что для всех х Ф х0, удовлетворяющих условию х х0 < 82, выполняется неравенство |fix) b2 < є (см. рис. 4.2):

Дх0 + 0)= lim Дх).

X->Xq + 0

Функция у fix) имеет предел в точке х0 тогда и только тогда, когда в этой точке существуют пределы как слева, так и справа и они равны, т.е. /(х0 0) -fixQ + 0).

Например, для функции /(х) = —^-77предел слева при х —> 0

1 + 2V*

равен единице: /(-0) = 1, а предел справа — нулю: /(+0) = 0 и, следовательно, lim fix) не существует (рис. 4.3).

х-»0

120

Рис. 4.3

4.15. Основные теоремы о пределах

Если функция у /(Af) -С (С — постоянная), то

lim f(M) = C.

Если lim /(Af) существует, то для любого числа к

М-*М0

lim kf(M) = k Urn f(M).

M^Mq m^>m0

Если существуют lim /(Af) и lim g(M),mo:

m^>m0 m^>m0

а) существует lim [f (M) + g(M)], причем

m-*m0

lim [f(M) + g(M)]= Urn /(Af) + lim g(Af);

M->M0 m-*m0 M->Mq

б) существует lim f(M)g(M), причем

m-*m0

lim [/(Af)g(Af)] = Urn /(Af) lim g(Af);

Af->Af0 m^>m0 m->m0

в) если lim g(Af) Ф О, существует lim f^Ml причем

' м^м06К ' * m^m0g(Af)

/(Af) _ m-»m0

lim /(Af)

lim

m->m0 g(M) lim g(Af)

Af —»Af0

4. Пусть /(Af) < g(Af) в некоторой окрестности точки AfQ. Тогда lim /(Af) < lim g(M), если эти пределы существуют.

М-¥Мд M-*Mq

121

В частности, если ДМ) < О (ДМ) > 0), то lim ДМ) < 0

М-*М0

( lim /(М)>0).

5. Если <р(М) < ДМ) < g(M) в некоторой окрестности точки М0 и lim ф(М) = lim g(M) = b, то lim f(M) = b.

M->Mq M->M0 M-*Mq

О Пример. Имеем

lim Xy lim x2

^ *1*2 _ x2->-l sj->-l _ 2" I"1.) __ ф

*i->2 x,2 + x2 Um x,2 + Um x2 22 + (-1)2 5'

X2~>-1 X2~»-l

4.16. Бесконечно малые и бесконечно большие функции

Функция у = а(М) называется бесконечно малой при М -> М0, если

lim а(М) = 0.

м->м0

В частности, функция у = а(х) называется бесконечно малой при х —> х0, если lim а(х) 0.

X-*Xq

О Примеры.

1. Функция а(х) Х , бесконечно малая при х -» 2, так как

X

х-2

lim —г— = 0. Данная функция является бесконечно малой также

*->2 х

при х —> °°, так как lim Х , = 0.

JC ~ X

2. Функция a(xl5x2) = — бесконечно малая при стремлеХ^ ~Ь Х-^

нии точки М(хр х2) к любой точке прямой х2 = Xj, за исключением начала координат О(0, 0). Функция а(хр х2) не имеет предела при M(xv х2) -> О(0, 0). •

Свойства бесконечно малых функций:

Г. Предел lim f(M) существует и равен числу b тогда и тольAf-»M0

ко тогда, когда ДМ) = Ь + а(М), где а(М) — бесконечно малая при М->М0.

122

2°. Сумма и произведение конечного числа бесконечно малых при М —> М0 функций являются бесконечно малыми функциями.

3°. Произведение бесконечно малой при М —> Af0 функции на ограниченную в некоторой окрестности точки М0 функцию является бесконечно малой функцией.

Функция у=/(Af) называется бесконечно большой при М—> Af0, если для любого числа К > 0 можно указать окрестность Sr(M0) точки М0 такую, что для всех точек Af є Sr(MQ), Мф Af0 выполняется неравенство |/(Af)| > К.

В этом случае пишут lim /(Af) = °° или /(Af) —> оо при Af-»Af0. м^м°

В частности, функция одной переменной у=fix) является бесконечно большой при х —> х0, если для любого числа К > 0 можно указать такое зависящее от ^положительное число 5, что для всех х ф х0, удовлетворяющих условию х xQ < 8, выполняется неравенство |/(х)| > К.

О Примеры.

х 2

1. Функция а(х) = —г— бесконечно большая при х —> 0, так как

X

lim а(х) -оо.

х-»0

Функция /(х) = бесконечно большая при х -> 1, так как

х-1

для любого ^Г> 0 найдется 8= 1/Х такое, что для всех хф ^удовлетворяющих условию |х 1| < /К, выполняется неравенство |/(х)| > К. При этом lim f(x) = -°o, lim /(х) = +°°.

х->1-0 х-»1+0

Функция /(Af) = —j—^—2 бесконечно большая при

Af-> 0(0,0), так как Urn /(Af) = +oo.*

v ' м-ко,оГ 7

Функция /(Af), /(Af) * 0 при Af ф Af0, является бесконечно большой при Af -> Af0 тогда и только тогда, когда функция a(Af) =

является бесконечно малой при Af —» AfQ.

Функция/(х) одной переменной является бесконечно большой при х -» оо, если для любого числа Z > 0 можно указать такое зависящее от L положительное число К, что для всех |х| > ^выполняется неравенство |/(х)| > L.

123

4.17. Сравнение функций. Эквивалентные бесконечно малые

Пусть функции /(х) и gix) таковы, что fix) Ф 0, gix) Ф 0 при х Ф х0

и существует предел Mm = /. Тогда: *->*<> gix)

а) если / Ф О и / Ф оо, то говорят, что функции fix) и gix) одного

порядка прих -> х0, и пишут/(х) = 0*(g(x));

б) если / = 1, то функции fix) и g(x) называют эквивалентными

при х —> х0 и пишут fix) ~ g(x);

в) если /= 0, то функцию fix) называют функцией более высокого

порядка малости по сравнению с функцией gix) при х -> х0 и пишут

/(х) = о(я(х)) (читается: «/(х) есть о малое or gix) при х —> х0»);

г) если / = оо, то gix) о(/(х)).

О Примеры.

sin2 X 1

1. sin2x = 0*(3х2) при х -> 0, так как lim — = -^0

х->о Зх2 3

(см. п. 4.11).

2. х = о(х2) при х —> оо, так как lim = 0. В то же время х2 = о(х)

х2

прих -» 0, так как lim— = 0. •

х->0 X

fix)

Если /(х) = 0*igix)) при х -» хп, т.е. lim ^ = / ^ 0, то /(х) ~ g(x)

х->х0 g(x)

и fix) = gix) + oigix)) при х -> х0.

Если fix) ~ и(х), a g(x) ~ v(x) при х —> х0, то при условии

.. и(х) /(х) существования lim —— существует и lim , причем

х->х0 v(x) х->х0 gix)

,. fix) ,. и(х) x^Xq g(x) х->х0 v(x)

О Примеры.

При а > 1 up > 0 функции logflx = оіхр) ихр = о(а*) прих -» оо, т.е. логарифмическая функция растет медленнее степенной функции, которая, в свою очередь, растет медленнее показательной функции.

Если ос(х) — бесконечно малая при х -» х0, то имеют место следующие эквивалентности:

124

sinoc(x) ~ a(x);

tga(x) ~ a(x);

arcsina(x) ~ a(x); arctga(x) ~ a(x); logjl + a(x)] ~ a(x)logae;

, . . a2(x)

1 cosa(x) ~ —y^-;

aa(x)-l~a(x)lna; [1 + a(x)]"-1 ~иа(х);

^1 + a(x) -1 ~ -a(x).

n

Указанные эквивалентности полезно использовать при вычислении пределов функций. Например,

е*2 -1 х2

Ит ^=== = lim—£ = -3;

*->оsinx(</l-X 1) х^°х.-(-Х)

Зх3-7х + 2 ,. Зх3 + о(Зх3) Зх3

lim з т = lim —л —^= Ит —г= -3. •

х^~4_бх + 9х -х *->°°-х +о(-х ) *-»~-х