5.14. теоремы о среднем для дифференцируемых функций

5.14. теоремы о среднем для дифференцируемых функций

Теорема Ролля. Если функция y=f(x) непрерывна на отрезке [а, 6], дифференцируема на интервале ]а, Ь[ и если f {a)=f (Ь), то на интервале ]а, Ь[ найдется хотя бы одна точка с такая, что Г(с)=0.

(in

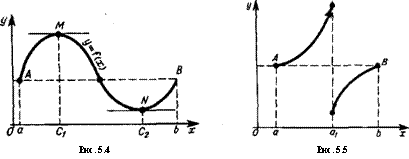Геометрически (рис. 5.4), в условиях теоремы, на графике функции f(x) (дуга АВ) найдется хотя бы одна точка, в которой касательная к графику параллельна оси Ох (это точки М и N). Условия теоремы существенны. Так, на рис. 5.5 функция /(х) разрывна в точке щ, а на рис. 5.6 функция f(x) не имеет в точке а2 производной (ни конечной, ни равной +оо, ни равной —со). В обоих случаях на отрезке [я, Ь] не существует ни одной точки, в которой /' (х)=0.

Теорема Лагранжа. Если функция у =/ (х) непрерывна на отрезке [а, Ь] и дифференцируема на интервале ]а, Ь[, то на интервале ]а, Ь[ найдется хотя бы одна точка с такая, что f(b)-f(a)=f (с)ф-а).

Геометрически (рис. 5.7), в условиях теоремы, на графике функции f(x) (дуга АВ) найдется хотя бы одна точка, в которой касательная параллельна хорде А В (это точки М и N).

Замечание. Полагая Ь=а+Ах, где АхфО, можно точку с представить в виде с=а+в ф-а)~а+в-Ах (0<6<1). Тогда формула f(b)—f (а) = /' (с) ф — а) принимает вид

/(a+Ax)—f (а)=Г (а + ВАх) Ах.

Это формула конечных приращений Лагранжа.

Если функция f (х) определена на некотором промежутке, непрерывна в каждом из концов этого промежутка (если он ему принадлежит) и имеет производную, равную нулю, во всех внутренних точках промежутка, то функция / (х) постоянна в промежутке (признак постоянства функции).

Теорема Кошм. Пусть функции ф (?) и ц> (t) непрерывны на отрезке [а, § и дифференцируемы на интервале ]а, /3[. Если производная <р' (0#0 при всех ґє]ос, <3[, то на интервале ]а, /J[ найдется хотя бы одна точка І такая, что

9(f)-9 (я) <р'Ц)

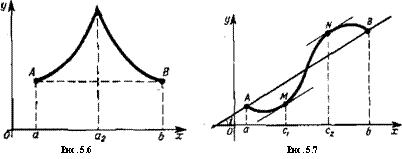Геометрический смысл теоремы Коши тот же, что и у теоремы Лагранжа. Действительно, если функцию (рис. 5.7) задать параметрически соотношениями х = (р (t), у = ф (t) (m^t^fi) так, что координаты точки А соответствуют значению t = a, а координаты точки В— значению ( = 0, то в точках М и N угловой

коэффициент касательной ~-~ равен угловому коэффициенту tg у

<р' (О

хорды АВ, где tg у = .

5.15. Формула Тейлора

Если функция у=/(х) имеет производные до (л 41)-го порядка включительно в некоторой окрестности точки х—а, то для всех х из этой окрестности справедливо равенство

ft ft J'W t л , Г (я) / 42 ,

...+'—^(*-в)Чд,(*),

л!

где

Д,(х) = --— (х-а) (0<В<))

(л+1)!

— остаточный член формулы Тейлора в форме Лагранжа.

Замечание. Полагая х=а + Ах, где Дх^О, формулу Тейлора можно представить в виде

f(a+Ax)-f(a) • Д*+~ ■ (Ах)2 + ...

...Н (Дх) Н (Дх)

л! (л + 1)! V '

(0<в<1),

обобщающем формулу конечных приращений Лагранжа. При в = 0 формула Тейлора принимает вид

1! 2! я!

<0<9<1)

(л + 1)! '

и называется формулой Маклорена.

Формулу Тейлора используют для представления функций многочленами, вычисления приближенных значений функций, при исследовании функций и вычислении пределов.

О Примеры.

1 і "

'Є*=1+Х + + -+...++ !\%, (Х).

2! 3! л!

cosx=l-+ --+ ... + (1)"-— + RM (х).

2! 4! 6! (2л)! 4 J

an-+ ... + (-1Г'-- + Rln(x).

З! 5! 7! (2л-1)!

(1+jc) = ] +тх- х2-к..

2!

...+^-ї14т-п+1)х+ЯАх).

In (l+x) = x-+ --+ ... + (-l)"_1 + R,(x). • 2 3 4 л

lim ф (x)=lim <р (х)= со, то при условии существования lim ——-.. * (х)

существует и lim , причем имеет место равенство

<р (х)

,. *W .. *'(х)

lim =lim

х~а <Р (X) <р' (х)

(правило применимо и в случае, когда а бесконечно).

Ф' (х)

Замечание. Если отношение в точке х = а также предч>' (*)

О оо

ставляет неопределенность вида или то при выполнении

О оо

соответствующих условий правило Лопиталя может быть приме-#'(*)

нено и к , так что

<р' W

ф(х) ф'(х) ф"(х)

lim = lim = hm *

х^в Ч> (х) х^а (?' (х) <р" (х)

причем процесс, если это необходимо, можно продолжить.

Неопределенности вида (Ооо) или (оо —оо) приводятся к неопределенностям или — с помощью алгебраических преоб0 оо

разований.

Неопределенности вида (1™), (оо°), (0°) приводятся к неопределенностям или (— } с помощью предварительного логарифо V00/

мирования. О Примеры.

limi^^^Vlim2^^-. х-,2 х2 + 7х~\&