5.19. наибольшее и наименьшее значения функции на множестве
5.19. наибольшее и наименьшее значения функции на множестве
Пусть функция y—f(x) определена на некотором множестве FeR1 и точка х<)Є V.
Если для всех хє V выполняется неравенство f(x)^f(x0), то говорят, что в точке Xq функция / (х) принимает свое наибольшее значение / (х0) на множестве V.
Если для всех хєУ справедливо неравенство /(x)^f (х0), то в точке х0 функция f(x) принимает свое наименьшее значение f(x0) на множестве V.
Если функция f(x) определена и непрерывна на отрезке [а, Ь], то она достигает на этом отрезке своих наибольшего и наименьшего значений, для определения которых необходимо найти все критические точки функции, принадлежащие отрезку [а, Ь], добавить к ним концы отрезка (точки х=а и х=Ь), найти значения
214
функции во всех выделенных точках и из полученных значений выбрать самое большое и самое маленькое.
Если же функция / (х) имеет на отрезке [а, Ь] конечное число точек разрыва, то для решения задачи отыскания наибольшего и наименьшего значений такой функции к указанным точкам необходимо добавить все точки разрыва функции, принадлежащие отрезку [а, Ь], и исследовать поведение функции в окрестности каждой точки разрыва.
Наконец, если функция / (х) задана на открытом промежутке (например, на интервале ]а, b[, а<Ь), то помимо исследования ранее указанных точек необходимо исследовать также поведение функции в односторонних окрестностях концов промежутка (при х-ю + 0 и при х-*Ь—0).
О Примеры.
1, Функция f (х)=х3 -Зх2 определена я непрерывна на отрезке [1, 3]. Ее производная /' (х) = 3х (х—2), так что точки х=0, х = 2 — стационарные. При этом, однако, х=0^[1, 3]. Следовательно, необходимо рассмотреть лишь точки х—, х = 2, х = 3. Имеем: /(1)= — 2, f{2)= — 4, /(3) = 0. Таким образом, наибольшее значение, равное нулю, функция принимает в точке х = 3, а наименьшее значение, равное ( — 4), — в точке х=2.
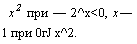 |
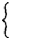 2. Рассмотрим функцию f(x) =
2. Рассмотрим функцию f(x) = Функция определена на отрезке [—2, 2], однако разрывна при х—0 (lim xz = 0, в то время как/(0) = — 1).
Стационарных точек функция f (х) не имеет, так как f (х)=2х при —2<х<0 и/' (х) = 1 при 0<х<2, т. е./' (х)ф0 на отрезке
[-2, 2].
Следовательно, необходимо рассмотреть лишь точки х= —2,
х = 0, х=2. Имеем: Л-2) = 4,/(0)=-1, 1™ f(x) = 0, f(2)= 1.
Таким образом, наибольшее значение, равное 4, функция принимает при х——2, а наименьшее значение, равное (— 1), — в точке х — 0.
3. Функция f(x)=4~х2 определена и непрерывна в полуинтервале [ — 2, 1[. Ее производная f(x)=— 2х, так что точка х=0— стационарная точка, принадлежащая [ — 2, 1[. Необходимо рассмотреть точки х= — 2, х = 0, х— 1. Имеем: /(—2) = 0,
/(0)=4, lim / (х) = lim (4—х2) = 3. Таким образом, наибольшее
Х-.1-0
х-*1~0
значение, равное 4, функция принимает при х = 0, а наименьшее значение, равное 0, — в точке х= — 2. # 5.20. Направление выпуклости графика функции
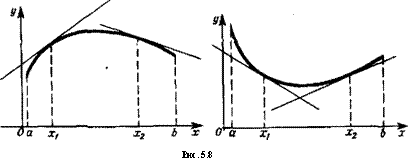
График дифференцируемой функции y=f(х) направлен выпуклостью вверх (выпуклостью вниз) на интервале ]а. Ь{, если в пределах этого интервала он расположен ниже (выше) касательной, проведенной в любой его точке (рис. 5.8).
Достаточное условие выпуклости
Пусть функция y=f(x) определена и дважды дифференцируема на интервале ]а, Ь[. Тогда:
 а) если f (х)<0 во всех точках интервала ]а, Ь[, то график функции/ (л:) направлен выпуклостью вверх на этом интервале;
а) если f (х)<0 во всех точках интервала ]а, Ь[, то график функции/ (л:) направлен выпуклостью вверх на этом интервале;
б) если f (х)>0 во всех точках интервала ]а, Ь[, то график функции f (х) направлен выпуклостью вниз на этом интервале. О Пример. Для функции / (х) = ъу/х • (х — 8) вторая производ4 jt + 4
ная f" (х) = • —=. Поэтому /" (х) < 0 при — 4 < х < 0 и, следовательно, на этом интервале график функции направлен выпуклостью вверх;/" (х)>0 на интервалах ]— оо, — 4[ и ]0, +со[; следовательно, на этих промежутках график функции направлен выпуклостью вниз, #
5.21. Точки перегиба графика функции
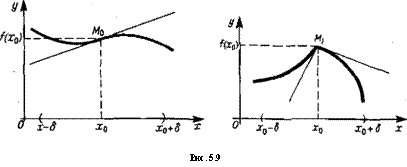
Точка (х0; / (;с0)) называется точкой перегиба графика функции y=f (х), если в этой точке существует касательная к графику и в промежутках ]х0 — S, х£ и ]х0, х0 + гДе ^ — некоторое положительное число, график функции имеет разное направление выпуклости.
Так, на рис. 5.9, а точка М0 является точкой перегиба графика функции, а на рис. 5.9, б точка Mt не является точкой перегиба, хотя в этой точке и происходит изменение направления выпуклости графика (в точке Л/| не существует касательной к графику).
Пусть точка (х0, /(хй)) является точкой перегиба графика функции y—f(x), определенной в некоторой окрестности точки х0. Тогда либо вторая производная /" (хй) не существует, либо /' (ло)=0 (необходимый признак точки перегиба).
 Пусть в точке (х0; / (х0)) существует касательная (хотя бы вертикальная) к графику функции у=/(х) и в некоторой окрестности ]х0—S, х0 + д (<5>0) существует /" (х), за исключением, быть может, точки х0, причем/" (хо)=0 илир (х0) не существует.
Пусть в точке (х0; / (х0)) существует касательная (хотя бы вертикальная) к графику функции у=/(х) и в некоторой окрестности ]х0—S, х0 + д (<5>0) существует /" (х), за исключением, быть может, точки х0, причем/" (хо)=0 илир (х0) не существует.
Если при этом в интервалах ]xa — S, х<Л и ]х0, х0+ё[ производная /" (х) имеет противоположные знаки, то точка (xa;f (х0)) является точкой перегиба графика функции y—f(x) (достаточные условия точки перегиба). О Примеры.
1. Рассмотрим функцию/(jc) = jc3. Ее производная/' (х)~ Ъхг,
а /" (х) = 6х. Тогда /" (х) = 0 при х=0, причем /' (0)~0 (в точке
х = 0 существует касательная к графику). Производная /" (х)<0
при х<0 и/" (х)> О при х>0. Следовательно, точка (0; 0) является точкой перегиба графика функции у=х3.
г- 4 х—2
2. Для функции / (х) — 3v'x (х — 8) имеем /'(jc) = _,
4 х + 4
f" (х)— =, так что/" (х) = 0 при х= — А и/" (х) не существует
4
при х=0. При этом /'(-4)= =, а р(0)-~оо (в точках
V2
х= —4 и х=0 существуют касательные к графику функции, причем при х=0 касательная вертикальна). Кроме того, /" (х)>0 прих<-4,/" (х)<Опри —4<дс<0и/" (х)>0прих>0. Следовательно, точки (—4; 12 3>/4) и (0; 0) являются точками перегиба графика функции. #
Обсуждение Справочник по математике для экономистов
Комментарии, рецензии и отзывы
