7.6. основные свойства определенного интеграла

7.6. основные свойства определенного интеграла

1°. При перестановке пределов интегрирования интеграл меняет знак на обратный:

]f(x)dx=-]f(x)dx.

а Ь

2°. Каковы бы ни были числа а, Ь, с, имеет место равенство

Ь с ь

]f(x)dx=f(x)dx + f(x) dx.

а а с 1

3°. Постоянный множитель можно выносить за знак определенного интеграла:

ъ ь ]Af(x)dx=Af(x)dx.

а а

4°. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:

ь ь ь ъ

] [f(x) + g(x)-h(x)]dx = lf(x)dx+lg(x)dxh(x)dx.

a ana

5°. Теорема о среднем значении. Определенный интеграл от непрерывной функции равен произведению длины промежутка интегрирования на значение подынтегральной функции при некотором промежуточном значении аргумента

]f(x)dx=(b-a)m,

а

где се]а, Ь{.

6°, Если F(x) — какая-либо первообразная от непрерывной функции f(x), то справедлива формула Ньютона — Лейбница

}f(x)dx = F(b)-F(a).

а

7.7. Вычисление определенных интегралов

Основным способом вычисления определенных интегралов является определение первообразной для подынтегральной функции и использование формулы Ньютона — Лейбница, которая может быть записана в виде

f(x)dx=F(x)

= F(b)-F(a).

Определение первообразной для многих функций может быть сложным процессом: не все функции имеют первообразные в виде элементарных функций. Поэтому для вычисления определенных интегралов используют приближенные формулы.

Разбивают отрезок интегрирования [а,Ь] на л равных частей длиной h = (b—a)jn и используют одну из следующих формул:

1) формула прямоугольников *

Jydjf=;A(y0+y1 + ...+yn_l);

2) формула трапеций ь

/Уо+Уп

/Уо+Уп

ydx

■+Уі+Уг + -+Ун-

3) формула парабол (Симпсона) (л — четное)

* h

ІУ йх^-<у0+4Уі +2у2+4у3 +... + 2у„_2+4ул_, +у„)

(чем больше л, тем точнее результат вычисления определенного интеграла).

7.8. Геометрические приложения определенного интеграла

Площадь криволинейной трапеции, ограниченной кривой y=f(x), осью Ох, прямыми х=а, х=Ь, находят по формуле

ь

S=jf(x)dx.

а

Объем тела, образованного вращением кривой y—f(x), ограниченной прямыми х=а, х = Ь при а<х<Ь, вокруг оси Ох, равен

Vx=njy2dx.

л

Объем тела, образованного вращением кривой х—<р(у), ограниченной прямыми у—с, y^dnpu c<y<d, вокруг оси Оу, равен

d

Vy=n[x2dy.

с

Длину дуги плоской кривой у=/(х), ограниченнной прямыми х=а, х=Ь, определяют по формуле

l=y/~Myfdx.

а

Площадь поверхности, образованной вращением кривой y=f(x), ограниченной прямыми х=а, х=Ь, вокруг оси Ох, равна

Sx=2nyyfT(yfdx.

а

Площадь поверхности, образованной вращением кривой х=ф{у), ограниченной прямыми у = с, y=d, вокруг оси Оу, равна

d

S^lnSxy/l + ixfdy.

с

7.9. Несобственные интегралы

Пусть функция f(x) определена и непрерывна на промежутке [а, + со[ (рис. 7.3). Рассмотрим интеграл $f(x)dx. Предел

а

Ь

lim f{x)dx

Ь-* + со а

называют несобственным интегралом первого рода от функции

+ »

f(x) на промежутке [а, + оо[ и обозначают J f(x)dx, т. е.

а

+ оо *

J f(x)dx= Urn lf(x)dx. Если указанный предел конечен, то говорят, что несобственный

+ 00

интеграл J f(x) dx сходится; если бесконечен или не существует, то расходится.

4 Ь

J /(jc)cLc= lim ff(x)dx.

а-* —со a

Пусть функция f(x) определена и непрерывна на интервале ] — со, + со[ и пусть точка се] — со,1 + со[. Тогда сумму

J f(x)dx+ lf(x)dx

(7.4)

называют несобственным интегралом первого рода от функции

+ 00

f(x) на интервале ]— со, +оо[ и обозначают _[ f(x)dx. Этот

интеграл сходится, если оба интеграла J f(x)dx, J f(x)dx

Г lim

J x *-. + a

сходятся. В этом случае сумма (7.4) не зависит от выбора точки с. О Примеры.

1.

і

lim d— lim In b (интеграл расходится).

J x »+ co

■ і

— = lim

l+Jt2 ■—CD

ao

= lim (arctg*-arctga)=

4-» +to

(интеграл сходится).

Пусть функция f(x) определена и непрерывна при а^х<Ь и не ограничена в любой окрестности точки х=Ь (рис. 7.5). Предел

«-.0 a

называют несобственным интегралом второго рода от функции fix) на промежутке [а, Ь{.

Если этот предел конечен, то несобственный интеграл

J/(x)djc=lim J f(x)dx

называют сходящимся; если беског нечен или не существует, то расходящимся.

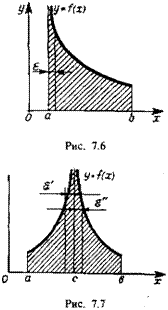
Аналогично определяют несобственные интегралы от функций, определенных и непрерывных при а<х^Ь (рис. 7.6):

ь ь J/(^)dJc=lim J f(x)dx.

a «-»0 д + «

Пусть функция f(x) определена и непрерывна на отрезке [а, Ь)> за исключением точки се]а, Ь[, в любой окрестности которой она не ограничена (рис. 7.7). Тогда несобственный интеграл от этой функции определяется как сумма двух несобственных интегралов на промежутках [а, с[ и ]с, Ь]:

}f(x) dx=]f (х) dx+1 f{x) dx.

Этот интеграл сходится, если оба слагаемых сходятся. О Пример.

dx

dx

+ lim J

d.v

= lim(-^V '+lim(—-V = lim(^-l) + hm(-l+-J

,<-.0 0 «'-ОХ 1+** i-oV / Ґ-А e"J

(интеграл расходится). #

7.10. Кратные интегралы

Двойной интеграл. Наряду с одномерным определеннь интегралом, называемым интегралом Римана, существуют дву! мерные и л-мерные (л-кратные) интегралы. Двумерный, или двойной, интеграл задается для функции двух переменных, явля-^ ющейся кусочно-непрерывной в квадрируемой области fl на плоскости Оху. Под квадрируемостью понимается существование общей числовой грани для бесконечного множества площадей многоугольников, описанных и вписанных в область Q.

Этот интеграл определяется как предел интегральных сумм aN, вычисляемых по формуле

oN=Ylf(Zi,Tli)&xfAyi,

где Ахі Ду(=Д5( — площади элементарных прямоугольников, составляющих конечное разбиение области &; л, — координаты точек Mh выбранных в указанных элементарных прямоугольниках.

Значение интеграла равно

I=\f(x, у)йх6у= lim (тл(Дх,-*0, Д>",—*0).

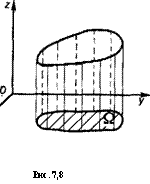
Двойной интеграл имеет геометрический смысл, выражаемый объемом криволинейного цилиндрического бруса, ограниченного поверхностью z=f(x, у), плоскостью Оху и вертикалями ц>( х, у)—6, исходящими из граничных точек области П на плоскости Оху (ряс. 7.8).

Основные свойства двойного интеграла

1°. Если область Q, в которой задана функция f(x, у), разбита

на две слагаемые части £lt и £12, то имеет место равенство

ЯД*, y)dxdy = а

^tffdxdy+tffdxdy.

О, Oj

2°. Постоянный множитель можно выносить за знак интеграла:

l(kj)dxdy~k fdxdy. а а

3°. Интеграл от суммы кусочно-непрерывных функций равен сумме интегралов от этих функций:

fiV+g)dxdy = Hfdxdy+flgdxdy. а по

4°. Если две функции fug связаны в области Q условием

vA/єП /(Л/)^(АГ>, то имеет место неравенство

\]fdxdy*k\gdxdy. а а

5°. Абсолютное значение интеграла удовлетворяет следующему неравенству:

|Цf{x.. у)dxdy*kЯf(x, У) |dxdy. а а

Теорема о среднем для двойного интеграла.

а) Определенный интеграл от кусочно-непрерывной функции

равен произведению площади области интегрирования Л на некоторое значение, лежащее между крайними значениями ти М подынтегральной функции:

ft fix, y)dxdy = p.Sim^u^M); о

б) в том случае, когда функция f(x, у) обладает непрерывностью в области П, это равенство принимает вид

ttf(x,y)dxdy=fiQS, где СеП. а

Вычисление двойного интеграла. Основной способ вычисления двойного интеграла — численное интегрирование с применением формул квадратурной аппроксимации, являющихся аналогами формул прямоугольников, трапеций и парабол, распространенных на области соответствующего профиля.

В качестве точных формул можно использовать формулы повторного интегрирования, сводящие двойной интеграл к следующим равенствам:

а) в области [а, Ь с, d], совпадающей с прямоугольником,

Я/(х, y)dxdy = dx fdy=]dy }/dx;

£1 а с с а

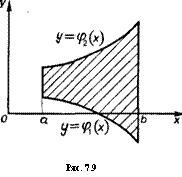
б) в области [a, b; <Ру(х), <р2(х)], совпадающей с трапецией

(рис. 7.9),

llf(x. y)dxdy=idx Y f(x, y)dy;

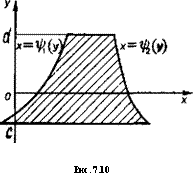
в) в области [ф1 (у), фг (у), с, d], совпадающей'с трапецией (ри .

7.10),

d

\f(x,y)dxdy=ldy J f(x,y)dx.

a c *м

Во всех остальных случаях составляют разбиение области S1 на элементарные прямоугольники и трапеции и используют аддитивные свойства интеграла.

л-кратные интегралы (основные понятия) при л>2. л-кратный интеграл определяется для функции « переменных, являющейся кусочно-непрерывной в измеримой л-мерной области П. Интеграл задается как предел интегральных сумм вида

і-і

где Ахц — приращения 1-й координаты в і-м элементарном л-мер-ном прямоугольнике; fл — значения 1-й координаты, выбранной в і-м элементарном прямоугольнике. Значение интеграла равно

J=lf{xt, хг, .... x„)dxidx2...dxn= lim <тн(Ахі~+0).

n-кратный интеграл не имеет простого наглядного геометрического смысла, но истолковывается как величина (л+ 1)-мерного объема в соответствующем пространстве.

Свойства п-кратных интегралов

На значения л-кратного интеграла переносятся все свойства двойных интегралов.

Теорема о среднем для л-кратного интеграла. На значение п-кратного интеграла переносится теорема о среднем в следующем виде:

а) JJ...$f(xu х2, .... x„)dx1dx2..dxn=ojp,

п

где (о — объем n-мерной области її; р. — среднее значение, лежащее между двумя крайними значениями т и М;

б) tf-JА*1> хг xn)dXi dx2... dx„~<of(C),

а

где СєП.

Вычисление и-кратного интеграла. Основной способ вычисления л-кратного интеграла — численное интегрирование с применением формул л-мерной квадратурной аппроксимации.

В качестве точных формул можно использовать формулы повторного интегрирования, сводящие кратный интеграл к следующим равенствам.

а) В п-мерном прямоугольнике [at, а2, b2 ...; а„,

ft, ft, ь„

Я...|/(х!,х2,....xn)dxidxz...dxH= Jdxt |dx2... f(xl,x2,....x„)dx„.

Примечание. В данной конфигурации допустимы произвольные перестановки порядка повторного интегрирования.

б) В п-мерной трапеции [а1( Ьх; аг, Ь2 ...; q>i (ху, ...,хв_|),

Ф2(х x„_S]

Я-№і^2 x„)dx,dx2...dx„ =

а

= Jdxjdx2... J f(xi,x2. x„)dxe.

Во всех остальных случаях область разбивают на элементарные л-мерные прямоугольники и трапеции и используют аддитивные свойства интеграла.

О Примеры.

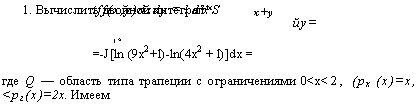
If , 9хЧі

= л: In

2V 4х* + 1

Ч 2

о О

9х2-И 4х" + 1

dx =

,37 г/ 1 1 ^ , 17 1 ^ 1

=1п —+ П ldx=ln~ + -arctg6 — -arctg4.

17 iV^ + l 4x2+J 37 3 2

2. Найти л-кратные интегралы для фунхций вида /(xlf х2, .... x„)=sm(x1 + x2 + ... + xx),

g(xlt х2, .... x„) = cos(x1 + x2 + ...+x„)1

Q — область типа n-мерного прямоугольника с ограничениями

а^х^^, а2^х2^Ьг а„<х„<£„. Имеем

Д...{Дхх, х2, x„)dx1dj:2...dxn=}djf, Jdx2... Jsinf £ x,ldx,,=

О Hi Oj a, /J /

=2"flsin sin,

/-і 2 L2'-i

l...g{xv хг, .... x„)dx1dx2...dj:„=Jdx1 Jdx2... Jcos( ^xJdx,,=2"flsin со.П£(«+*Д f-i 2 L2'-i J

Примечание. Доказательство проводится методом индукции. Прил=1 /= sinх, g—cosх, smxdx=cosa — cosb=z2sm sin

І 2 2

г . ... „ . Ь—а а+Ь

I cosjcdjc=sino — sin a=2 sin cos

І 2 2