1.19. графики элементарных функций
1.19. графики элементарных функций
Целая рациональная функция (многочлен)
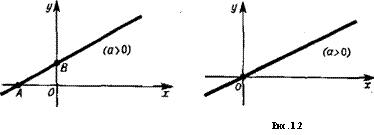
а) Линейная функция у= ах + Ь (рис. 1.1). Графиком этой функции является прямая линия. Функция возрастает при а> О и убывает при а<0. Оси координат пересекаются прямой в точках
А (^~~> ®j и В (0* b)^ слу4^ ^=0 получаем прямую пропорциональность у = ах (рис. 1.2). График функции проходит через начало координат.
Рис. 1.1
 |
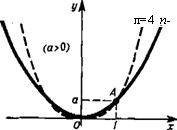
функции является парабола с осью симметрии, параллельной оси
 | |||
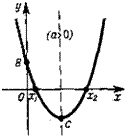 | |||
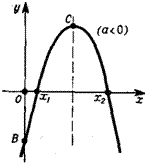
>рдинат. При а>0 ветви параболы направлены вверх, при к 0 — вниз. Ось ординат пересекается кривой в точке В (0; с).
їершина параболы С имеет координаты ( ; .Абсциссы
2а 4в J
с,, х7 точек пересечения параболы с осью Ох определяют по
 . Веформуле хк 2~2а
. Веформуле хк 2~2а
личины X] и х2 являются корнями квадратного уравнения ах2 + bx + c = Q в том случае, когда оно имеет решения на множестве действительных чисел.
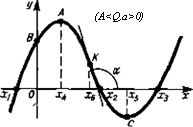
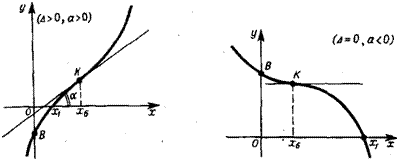
в) Многочлен третьей степени y=*ax3 + bx2 + cx + d (рис. 1.4). Графиком функции явля-
л=5IIn-З
(а>0)
 | |||
 |
ется кубическая парабола. Поведение функции зависит от знаков а и Д = 3дс—b2. В случае Д^О функция возрастает при а>0 и убывает при о<0. Если же А<0, то функция имеет одну точку максимума и одну точку минимума. Кубическая парабола имеет одну точку перегиба К. Ось ординат пересекается кривой в точке В (0; d). Абсциссы точек максимума и минимума х4 и х$ определя-
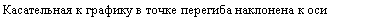 ют по формуле х = Ь
ют по формуле х = Ь
3d
За
Абсцисса точки перегиба хь равна
Ох под углом а таким, что tga=
За
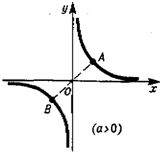
г) Степенная функция у=ах (п> 1 — целое) (рис. 1.5).
Графиком функции является парабола л-го порядка, которая проходит через точки О (0; 0) и Л (1; а) и касается оси Ох в начале координат. При п четном график функции симметричен относите-
(а «У
Рис: 1.6
льно оси Оу ив начале координат имеет минимум при а>0 и максимум при а<0. При п нечетном график функции симметричен относительно начала координат, которое является точкой перегиба графика.
Дробно-рациональная функция
а) Обратная пропорциональа
ность у = (рис. 1.6). Графиком
функции является равносторон'*ИС1-7
няя гипербола, ветви которой симметричны относительно начала координат. Оси координат служат асимптотами графика. В слу
чае а>0 гипербола имеет вершины в точках А (у/а;' у/а), В ( — у/а; -у/а). В случае а<0 вершины имеют координаты Л (~у/а\; у/а), В (у/а\; -у/а).
bx ~t~ Ь
б) Дробно-линейная функция у — (рис. 1.7). Графиком
cx + d
функции является равносторонняя гипербола. Асимптотами слуd а жат прямая х= — , параллельная оси Оу, и прямая у = -, параден с
лельная оси Ох. Расположение ветвей гиперболы зависит от
be —ad
знака величины Д= .
с* а
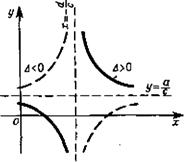
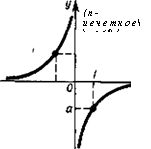
в) ' Степенная функция у = — (л> 1 — целое) (рис. 1.8). ГрафиX
 | |||
 | |||
 -/ О
-/ О /п-четное) ( а>0 J
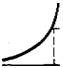
 ком функции является кривая гиперболического типа, проходящая через точку (І; а). Оси координат служат асимптотами графика. При п четном график симметричен относительно оси Оу, при л нечетном имеет место симметрия относительно начала координат.
ком функции является кривая гиперболического типа, проходящая через точку (І; а). Оси координат служат асимптотами графика. При п четном график симметричен относительно оси Оу, при л нечетном имеет место симметрия относительно начала координат.
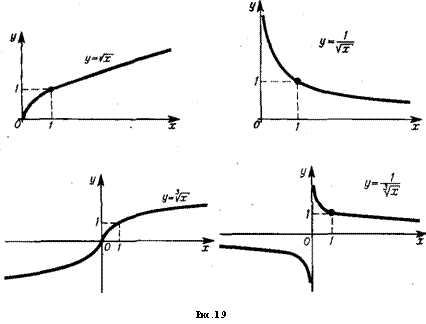
Некоторые иррациональные функции (рис. 1.9). Показательные и логарифмические функции
а) Показательная функция у — а (а > 0, а Ф1) (рис. 1.10). \% -График функции при любом а проходит через точку (0; 1)
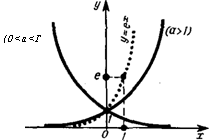 и асимптотически приближается к оси Ох. Функция принимает только положительные значения.
и асимптотически приближается к оси Ох. Функция принимает только положительные значения.
б) Логарифмическая функция у — о\%„х{а>0, аф) (рис.
1.11). График функции при любом а проходит через точку (1;
0) и асимптотически приближается к оси Оу. Функция определена только для положительРис. l.io ных значений аргумента х.
Рис. 1.11
Рис. 1.12
Замечание. Важное место в исследованиях многих явлений (в частности, экономических) занимают показательная функция
у=е* и логарифмическая функция у=ах (у = о^х). Число е — иррациональное (еж2,72).
в) Кривая Гаусса j=e (рис. 1.12). График функции имеет одну точку максимума Л (0; 1), две точки перегиба В—;
и С — ), симметричен относительно оси ординат
>/«/ V у/2 v/e/
и асимптотически приближается к оси абсцисс. Тригонометрические функции
а) Синус и косинус: y~sinx и y=cosx (рис. 1.13). Функции sin х и cos х периодические с периодом 2л.
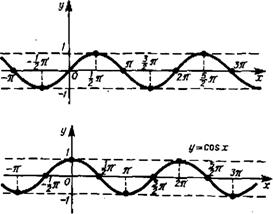
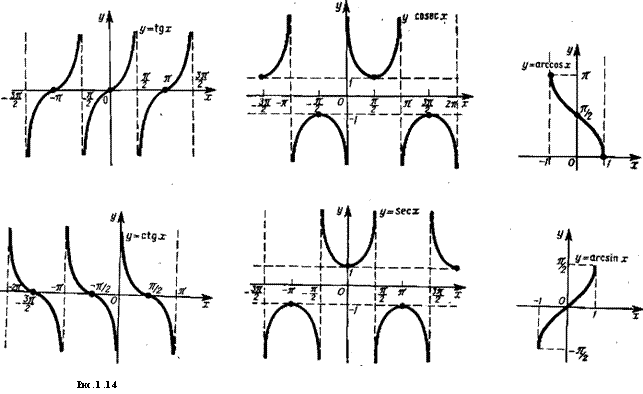
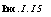 Рис. 1.16
Рис. 1.16
б) Тангенс и котангенс: y=tgx и y=ctgx (рис. 1.14). функции
tgx и ctgjc периодические с периодом 71.
в) Секанс, косеканс: y = secx и ^=cosecx (рис. 1.15);
sec х = 1 , cosecx=^-. Функции secx и cosec х периодические
cos х sin X
с периодом 2я.
Обратные тригонометрические функции
а) Арксинус и арккосинус: j> = arcsin;c и у = arccos х (рис. 1.16), Функция j=arcsinx каждому действительному числу
хє[— 1, 1] ставит в соответствие угол уе — -, - такой, что
sin V—х. Например, arcsin -=-, так как sin -=-.
2 6 6 2
Функция у=arccos х каждому действительному числу
хє[—1, 1] ставит в соответствие угол у є [0, я] такой, что cosy = x.
Я It 1
Например, arccos = -, так как cos = -.
3 3 2
б) Арктангенс и арккотангенс: y = arctg.x и j> = arcctgx (рис. 1.17). Функция y=arctgx каждому действительному числу хє] — оо, + оо[ ставит в соответствие угол уе] — я/2, я/2[ такой,
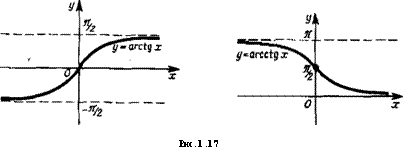 что tgy=x. Например, arctgv/3 = re/3, так как tg (я/3) = ч/з.
что tgy=x. Например, arctgv/3 = re/3, так как tg (я/3) = ч/з.
Функция у arcctgx каждому действительному числу хє] — оо, + со[ ставит в соответствие угол ує]0, я[ такой, что ctgy = x. Например, arcctg 1 = я/4, так как ctg (я/4) = 1.
1.20. Примеры неэлементарных функций и важнейших кривых
Неэлементарные функции
а) у=[х] (читается: «у равно антье х»)— целая часть х. Определяется как наибольшее целое число, не превосхо-
| 2 1 | St і і *i | I y-signx |
| і ! і J | X | |
| ! 0 і | ^ J J | |
| -/ |
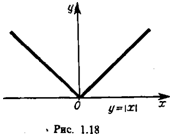 |
б) у — sign jc (читается: «у равно сигнум х») — знак числа х (рис. 1.18):
'— I, если :с<0, sign;c=^ 0, если х = 0, 1, если х>0.
в) У= W — абсолютная величина (модуль) х (рис. 1.18):
х, если х>0, —лг, если х<0.
Важнейшие кривые
Xі у1
а) Эллипс — Н—= 1 (рис. 1.19).
й2 AJ
Xі у1
б) Гипербола——-=1 (рис. 1.20). а2 А2
в) Парабола х2 = 2ру или у2 = 2рх (рис. 1.21)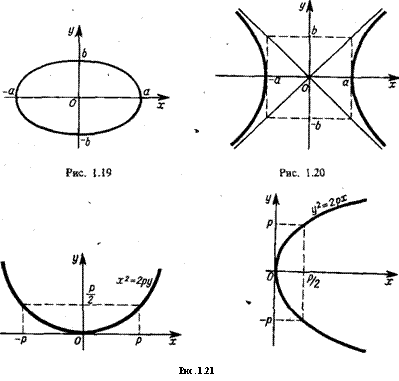
іШшятие множества
Понятие «мводквстваожервичных (неопределяемых) понятий математики. Описательно термин «множество» объясняется как совокупность, коллекция, набор некоторых объектов произвольной природы, объединенных по каким-то общим для них признакам. Объекты, из которых состоит множество, называют его элементами ((ёюмволга^еская запись ай означает принадлежность элемента а множеству А. Запись афАячает, что элемент а не принадлежит множеству А.
Множество А называют подмножеством другого множества Д если каждый элемент множества А является одновременно элементом множества В. В этом случае пишут А Ф (читается: «включается или содержится в В»).
Множества А и? равны (А =В) тогда и только тогда, когда А <Ви В Apr. е. если эти множества состоят из одних и тех же элементов.
Множество, не содержащее ни одного элемента, называется
пустым и обозначается символом 0. Любое множество содержит 0 в качестве подмножества. Очевидно, А а А; А и 0 называют несобственными подмножествами множества А. Все
остальные подмножества множества А называют собственными. „ '
Множество А элементов х, обладающих свойством Р (х), символически записывают в виде А = {х Р(х)}. Например, А = = {х x=2k, к=1, 2, ...} означает, что множество А состоит из четных положительных целых чисел 2, 4, 6, 8, ... .
Обсуждение Справочник по математике для экономистов
Комментарии, рецензии и отзывы
