8.10. авторегрессионная условная гетероскедастичность (аруг)*)

8.10. авторегрессионная условная гетероскедастичность (аруг)*)

В оригинале англоязычная аббревиатура — это ARCH, что соответствует "AutoRegressive Conditional Heteroskedasticity" (примеч. научн. ред. перевода).

В финансовых временных рядах часто наблюдается феномен, который называется объединением в кластеры волатильности

(изменчивости). В этом случае большие возмущения (остатки) имеют тенденцию к последующим большим возмущениям в любом из двух направлений, а малые возмущения имеют тенденцию к последующим малым возмущениям. Например, фондовые биржи обычно характеризуются периодами высокой волатильности и более «ослабленными» периодами низкой волатильности. Это особенно верно для краткосрочной периодичности, например, в ежедневных или еженедельных отчетах, но менее ясно для более долгосрочной периодичности. Один из способов моделировать такие структуры состоит в том, чтобы принять предположение зависимости дисперсии остатков St от ее предыстории.

8. 70. 7. АРУГи ОАРУГ-модели*)

Основополагающей статьей в этой области является статья Энгле (Engle, 1982), в которой вводится понятие авторегрессионной условной гетероскедастичности (АРУГ). Смысл понятия состоит в том, что дисперсия остаточного члена в момент времени t зависит от квадратов остаточных членов из предыдущих периодов. Самая простая форма имеет вид

о= Д{є?|2і_і} = w + о4_і, (8.90)

где lt-і обозначает информационное множество, обычно включающее St-i и всю его предысторию. Такая спецификация называется процессом авторегрессионной условной гетероскедастичности порядка 1, АРУГ(1). Чтобы гарантировать, что а2 > 0 вне зависимости от е2_х, мы должны наложить ограничения w > 0 и a > 0. Моделью АРУГ(1) описывается следующее: если в периоде t — l случается большое возмущение, то более вероятно, что St также имеет большое (по абсолютной величине) значение. Таким образом, когда є2_± является большим, дисперсия следующего остатка et является также большой.

Спецификация модели (8.90) не означает, что процесс St является нестационарным. Просто подразумевается, что значения квадратов е2 и е2_х коррелированны. Безусловная дисперсия St имеет вид:

Англоязычная версия ОАРУГ-модели — это GARCH-Model, Generalized ARCH-Model (примеч. научн. ред. перевода).

a2 = E{s2t} = w + aE{e2t_1}

и для стационарного временного ряда имеет решение

1-а

при условии, что 0 < а < 1. Заметим, что безусловная дисперсия не зависит от момента времени t.

Модель АРУГ(1) легко расширяется на процесс АРУГ(р), который можно написать как

а2 = из + ols+ а2є2_2 + • • • + ар^і-р = ія + а(Ь)є2_г, (8.92)

где a(L) — полином от оператора сдвига порядка р — 1. Чтобы гарантировать не отрицательность условной дисперсии, ти, должны быть неотрицательными и коэффициенты в a(L). Чтобы обеспечить стационарность процесса, требуется также, чтобы а3< 1, j = 1, 2,... ,р. Влияние et-j (при сдвиге на j периодов назад) на текущую волатильность определяется коэффициентом otj. В модели АРУГ(р) старые возмущения более чем на р периодов ранее не имеют никакого эффекта на текущую волатильность.

Присутствие ошибок АРУГ в регрессии или модели авторегрессии не лишают законной силы МНК-оценивание. Однако предполагается, что существуют более эффективные (нелинейные) методы оценивания, чем обычный метод наименьших квадратов. Более важным является возможность предсказывать будущие дисперсии, например, потому что они могут соответствовать степени рискованности инвестиций. Следовательно, уместно тестировать наличие эффектов АРУГ и, если требуется, оценивать модель с учетом этого. Тестирование на авторегрессионную гетероскедастичность порядка р можно провести последовательно с помощью теста на гетероскедастичность Бреуша—Пагана (Breusch—Pagan), обсужденного в главе 4. Достаточно построить вспомогательную регрессию квадратов МНК-оцененных остатков е2 по лагированным квадратам •.. , е2_р и константе, и вычислить Г раз В2. При нулевой гипотезе гомоскедастичности (#! = ... = ар = 0) полученная в результате критическая статистика асимптотически имеет хи-квадрат распределение с р степенями свободы. Другими словами, тестирование гипотезы гомоскедастичности против альтернативной гипотезы, что ошибки следуют процессу АРУГ(р), очень простое.

Модели АРУГ обобщались по-разному многими способами. Полезной модификацией является обобщенная модель АРУГ или модель О АРУГ, предложенная Боллерслевом (Bollerslev, 1986). В общей форме модель ОАРУГ (р, q) можно написать как

Р я

3 = 1 3=1

или

a2 = w + аЩе2^ + {3{L)o2_x (8.94)

где a(L) и (3{L) — полиномы от оператора сдвига. На практике спецификация ОАРУГ (1, 1) часто выполняется очень хорошо. ОАРУГ (1, 1) можно записать в виде

а2 = w + ае2_г + (За2_х (8.95)

где для оценивания имеется только три неизвестных параметра. Для неотрицательности а2 требуется, чтобы ти, а и (3 также были неотрицательны. Если мы определим щ = s2 — а2, то процесс ОАРУГ(1, 1) можно переписать как

є2 = w + (а + (3)е2_х +vt&vt-,

который показывает, что квадраты ошибок следуют процессу АРСС(1,1). Несмотря на то, что ошибка щ является сериально некоррелированной, она является гетероскедастичной. Коэффициент компоненты авторегрессии равен а + /3, поэтому для стационарности требуется, чтобы а + /3 < 1. Значения а + j3 близкие к единице подразумевают высокое постоянство в волатильности Х1 Заметим 12 что при условии стационарности остатков должно выполняться

Е{е2_1} = Е{о2_1} = а2, и тогда безусловную дисперсию St можно написать в виде

а2 = w + аа2 + (За2

или

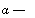2 W

а-(3

(8.96)

Процесс интегрированной ОАРУГ (1, 1) или ИОАРУГ(1, 1) возникает, когда a -fj3 = 1 и возмущения волатильности имеют постоянный эффект (см. Engle, Bollerslev, 1986).

Равенство, которое следует, справедливо, если только et не имеет автокорреляции.

Мы можем рекурсивно подставлять лаги в выражение (8.95), чтобы получить соотношение

a2 = w(l + /3 + (32 + ...) + а(е2_1 + /3є2_2 + (32є2_3 + ...) =

оо

= ^V*E/^l£^, (8-97)

которое показывает, что спецификация модели ОАРУГ(1, 1) эквивалентна спецификации модели АРУГ бесконечного порядка с геометрически убывающими коэффициентами. Это означает, что эффект возмущения на текущую волатильность уменьшается с течением времени. Следовательно, спецификация процесса ОАРУГ может обеспечить экономную альтернативу процессу АРУГ высшего порядка. Уравнение (8.97) можно также переписать в виде, удобном для прогнозирования:

оо

о*-*2 = а£р-є*ч-о*). (8-98)

3 = 1

В литературе предложено много альтернативных спецификаций для моделирования условной волатильности, которые соответствуют различным акронимам (для обзора см. Bollerslev, Chou, Kroner, 1992; Bera, Higgins, 1993; Bollerslev, Engle, Nelson, 1994; Diebold, Lopez, 1995). Важным ограничением вышеприведенных спецификаций моделей АРУГ и ОАРУГ является их симметрия: имеют значение только абсолютные значения возмущений, а не их знак. Таким образом, большое отрицательное возмущение имеет то же самое воздействие на будущую волатильность, что и большое положительное возмущение той же самой величины. Содержательное обобщение находится в направлении асимметричных моделей волатильности, в которых положительные и отрицательные возмущения одной и той же величины имеют разное воздействие на будущую волатильность. Заметим, что различие между положительными и отрицательными возмущениями более ощутимо для фондовых бирж, чем для обменных курсов, где агенты обычно находятся по обе стороны рынка. Таким образом, положительные возмущения для одного агента могут быть отрицательными возмущениями для другого.

Асимметричная модель должна учитывать возможность того факта, что неожиданное снижение цены («плохие новости») имеет большее воздействие на будущую волатильность чем неожиданное увеличение цены («хорошие новости») на ту же величину. Основополагающий подход, улавливающий такие асимметрии, представлен моделью экспоненциальной ОАРУГ или ЭОАРУГ Нельсона (Nelson, 1990), которая имеет вид

log a2 = w + Р log a2_, + 7— + (8.99)

где a, j3 и 7 — постоянные параметры. Так как модель ЭОАРУГ включает уровень et-/crt--> то она асимметрична поскольку 7^0. Когда 7 < 0, то положительные возмущения порождают меньшую волатильность, чем отрицательные возмущения («плохие новости»). Включением дополнительных лагов возможно получить расширение модели ЭОАРУГ. Заметим, что можно переписать модель (8.99) в виде:

log a2 = w + /3 log a2_x + (7 + a)——, если > 0,

log of = t*7 + f3 log cr^_! + (7 — a)^—L? если < 0.

0"t-i

Логарифмическое преобразование гарантирует, что дисперсии никогда не будут отрицательными. Обычно следовало бы ожидать, что 7 + a > 0, несмотря на то, что 7 < 0.

Энгле и Нг (Engle, Ng 1993) охарактеризовали диапазон альтернативных моделей для условной волатильности так называемой кривой воздействия новостей, которая описывает воздействие последнего возмущения доходности (новости) на текущую волатильность (содержащую всю информацию, датированную t — 2 или ранее, в виде константы и фиксации всех лагированных условных дисперсий в безусловной дисперсии а2). По сравнению с моделью ОАРУГ (1, 1) модель ЭОАРУГ имеет асимметричную кривую воздействия новостей (с более высоким воздействием для отрицательных возмущений). Кроме того, поскольку эффект на а2 экспоненциальный, а не квадратичный, кривая воздействия новостей модели ЭОАРУГ как правило имеет более крутые наклоны (см. Engle, Ng, 1993).

Финансовая теория говорит нам, что определенные источники риска оцениваются рынком. То есть, активы с большим количеством «риска» могут обеспечить более высокую среднюю доходность для их компенсации. Если а2 является подходящим измерителем риска, то условная дисперсия может быть одним из факторов, определяющих условное среднее значение функции yt. Один из вариантов модели АРУГ — модель аруг-в среднем или аруг-С Энгле, Лилина и Робертса (Engle, Lilien, Roberts, 1987) специфицируется в виде

yt = х[6 + Ьа + st,

где St описывается процессом АРУГ(р) (с условной дисперсией of). Кампбелл, Ло и МакКинлей (Campbell, Lo, MacKinlay, 1997, Section 12.2) представили дополнительное обсуждение взаимосвязей между моделями АРУГ-С и моделями ценообразования активов, подобных модели оценки финансовых активов, обсужденной в параграфе 2.7.

8.10.2. Оценивание и прогнозирование

Существуют различные подходы к оцениванию условных моделей волатильности. Предположим, что St — остаточный член модели типа13) yt = х[6 + £t, где xt может включать лагированные значения yt. В качестве частного случая xt является просто константой. Кроме того, пусть условная дисперсия et описывается процессом АРУГ(р). Теперь, если мы сделаем предположения об (условном) распределении et, то мы можем оценить эту модель методом максимального правдоподобия. Чтобы понять, как это делается, положим:

st = (JtUt с i/t~ НОНР(0,1)*

Это означает, что условное (по информации It-i) распределение возмущения et является нормальным со средним нуль и дисперсией of. Однако это не подразумевает, что безусловное распределение St является нормальным, поскольку at может быть случайной переменной, если мы не накладываем условие Xt-i • Как правило, безусловное распределение имеет более тяжелые хвосты, чем нормальное распределение. Поэтому мы можем записать условное распределение yt как

/Ы1"г'-1)=7щехрН(!)}'

где

Чтобы избежать путаницы с параметрами ОАРУГ коэффициенты регрессии обозначаются в.

Напомним, что НОНР(а, а2) — это «Независимые Одинаково Нормально Распределенные» случайные величины со средним значением а и дисперсией а2 (примеч. научн. ред. перевода).

of = w + ole + ... + ape2_p и et = ytx't9.

Отсюда логарифмическую функцию правдоподобия можно определить как сумму (по всем t) логарифмов вышеприведенного выражения, подставляя соответствующие выражения для о и St Логарифмическую функцию правдоподобия можно максимизировать обычным способом относительно аь ... , ар и zd. Наложение условий р

стационарности (^Г^ otj < 1) и неотрицательности (ау > 0 для всех j)

может быть трудным на практике, поэтому большие значения для р не рекомендуются.

Если vt не имеет в точности стандартного нормального распределения, то вышеприведенная процедура максимального правдоподобия может дать состоятельные оценки для параметров модели, несмотря на то, что функция правдоподобия при этом специфицирована некорректно. Причина состоит в том, что при некоторых довольно слабых предположениях условия первого порядка процедуры максимального правдоподобия справедливы также, когда щ не имеет нормального распределения. Такой метод оценивания называется методом максимального квазиправдоподобия (см. параграф 6.4). Однако для вычисления стандартных ошибок оценок следует сделать некоторые корректировки (подробности см. у Hamilton, 1994, р. 663).

В вычислительном отношении более простой подход был бы осуществлен с помощью ОМНК (см. главу 4). В этом случае, во-первых, 9 оценивается состоятельно применением обычного МНК. Во вторых, поскольку строится регрессия квадратов МНК-оцененных остатков е2 по е^_1?..., е2_р и константе, то она является той же регрессией, которая используется для вышеописанного теста гетероскедастичности. Расчетные значения из этой регрессии являются оценками для g и могут использоваться для преобразования модели и вычисления оценки взвешенных наименьших квадратов (РОМНК-оценки) для 9. Этот подход работает хорошо, только если расчетные значения для о все строго положительны. Кроме того, подход не приводит к асимптотически эффективным оценкам для параметров АРУГ.

Прогнозирование условной дисперсии из модели АРУГ(р) осуществляется напрямую. Чтобы пояснить это, перепишем модель «в отклонениях от средних» в виде:

2 2 /2 2 , , / 2 2 2 ^

a -а = а^е^-а ) + ...+ap(et_р-<т ) с а =- .

у 1 — а — ... — аю

Предположив для удобства обозначений, что параметры модели известны, получим прогноз на один период вперед

^t+ii* = £{4fїї2*} = v2 + ai(e2t °2) + • • • + *2)Это аналогично прогнозу, получаемому с помощью модели АР(р) для yt, как обсуждалось в параграфе 8.8. Прогноз условной волатильности более чем на один период вперед можно получить, используя рекурсивную формулу

ahh = E{e1+hlt} = <J2 + M<rt2+h-i|t - + • • • + api^t+h-plt ~ а2)і

где &t+j — £2+j если J < 0. Прогноз на /і-периодов вперед сходится к безусловной дисперсии а2, если h становится большим (предполагая, что ai + ... + ар < 1).

В случае модели ОАРУГ прогнозирование и оценивание можно осуществить таким же образом, если мы используем выражения (8.97), (8.98) или обобщение более высокого порядка. Например, прогноз на один период вперед с помощью модели ОАРУГ (1, 1) имеет вид

(J2t+l = (J2 + {a + (5){a2-a2),

где

оо 3 = 1

Прогноз на /і-периодов вперед можно написать как

<T?+hlt = <T2 + (a + (3)h(a?-a2).

Из последнего выражения видно, что прогнозы волатильности сходятся к безусловной дисперсии со скоростью а + р. В случае моделей ЭОАРУГ оценивание можно выполнить также методом максимального правдоподобия, хотя простые выражения в аналитическом виде для прогнозов на /г-периодов вперед недоступны. Эмпирически функция правдоподобия для модели ЭОАРУГ более трудна для максимизации и иногда имеют место проблемы отсутствия сходимости.

8. /0.3. Пример: волатильность в ежедневных обменных курсах

Для того, чтобы проиллюстрировать некоторые обсужденные выше модели волатильности, мы рассмотрим ряд ежедневных обменных курсов между долларом США и немецкой маркой за период с 1 января 1980 по 21 мая 1987. За исключением дней, в течение которых

-0.04 1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

500 1000 1500

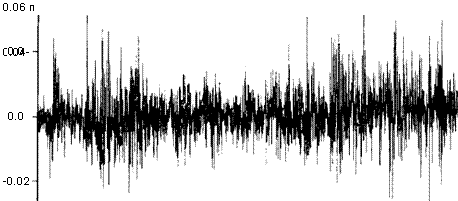
Рисунок 8.10. Ежедневные приращения логарифма обменного курса (доллары США к немецким маркам), 2 января 1980 г. 21 мая 1987 г.

нет котировальных цен (Новый год и т.д.), в итоге имеем Г = 1867 наблюдений. Поскольку логарифмы обменных курсов приближенно аппроксимируются процессом случайного блуждания, мы рассматриваем модель, в которой yt является приращением логарифма обменного курса, а условное среднее включает только свободный член. Временной ряд для yt представлен графиком на рисунке 8.10 и показывает существование периодов с низкой волатильностью и периодов с высокой волатильностью.

МНК-оцененные остатки et построенной регрессии yt по константе, конечно, представляют собой значения yt минус их выборочное среднее. На основе этих остатков мы можем выполнить тесты для эффектов АРУГ, построив регрессию е2 по константе и р лагирован-ным возмущениям. Проверка гипотезы гомоскедастичности против ошибок АРУГ(1) дает критическую статистику (вычисленную как Г, умноженное на R2 вспомогательной регрессии), равную 21,77, которая является высоко значимой для распределения хи-квадрат с

одной степенью свободы. Аналогично мы можем проверить гипотезу гомоскедастичности против ошибок АРУГ(6) со статистикой, равной 83,46, которая также приводит к явному отклонению предположения гомоскедастичности.

Стандартное программное обеспечение для этих моделей доступно, например в MicroFit или ЕViews. В зависимости от рутинных методов оптимизации, начальных значений и критериев сходимости, используемых в этих программах, результаты оценивания могут немного различаться.

Оценивались следующие три модели: АРУГ(6), ОАРУГ(1, 1) и стандартная экспоненциальная модель ОАРУГ14) (ЭОАРУГ(1, 1)). Результаты оценивания представлены в таблице 8.6. Все специфицированные модели оценивались методом максимального правдопо

добия, предполагая, что условное распределение ошибок нормально. Результаты для спецификации АРУГ(6) показывают, что все

лагов имеют значимый и положительный эффект. Кроме того, оказалось, что коэффициенты не снижаются до нуля очень быстро. Более экономная модель ОАРУГ (1. 1) также показывает, что вияние лагированных возмущений снижается очень медленно. Оцененное значение a + /3 равно 0,976, так что оцененный процесс близок к нестационарному процессу. Для экспоненциальной модели ОАРУГ, мы не находим свидетельства асимметрии, поскольку коэффициент

имеет t-отношение, равное только —1.37. Как показано выше, это не является необычным открытием для обменных курсов. Большой коэффициент для log of также отражает высокую степень постоянства в волатильности обменного курса.

ARCH6 EGARCH11 GARCH11

Рисунок 8.11. Условные стандартные отклонения, получаемые из разных моделей, 1 января 21 мая 1987 г.

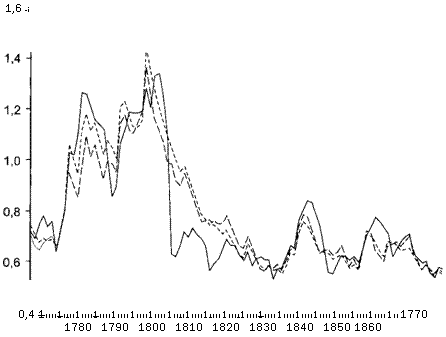минимизировать воздействие начальных условий и оценить различие моделей, мы представили результаты только для последних пяти месяцев 1987 г. На графике видно, что волатильность, предполагаемая спецификацией модели АРУГ(б) менее гладкая, чем для спецификацией моделей ОАРУГ(1, 1) и ЭОРУГ(1, 1). Очевидно, что шесть лагов недостаточны, чтобы зафиксировать постоянство волатильности.