9.5. коинтеграция: многомерный случай

9.5. коинтеграция: многомерный случай

Когда включается больше двух переменных, анализ коинтеграции несколько более сложен, потому что в этом случае обобщением коинтегрирующего вектора является коинтегрирующее пространство, размерность которого априори не известна. Таким образом, когда мы имеем множество из к переменных /(1), то может существовать вплоть до к — 1 независимых линейных соотношений, которые являются /(0), в то время как любая линейная комбинация этих соотношений, по построению, также является /(0). Это означает, что индивидуальные коинтегрирующие векторы статистически больше не идентифицируемы; а есть только пространство, натянутое на эти векторы. В идеале, в коинтегрирующем пространстве можно найти векторы, которые имеют экономическую интерпретацию и могут интерпретироваться как представляющие долгосрочное динамическое равновесие.

9.5.1. Коинтеграция в векторных моделях авторегрессии

Если интересующие нас переменные образуют fc-мерный вектор Yt, элементы которого предполагаются /(1), то могут быть различные векторы (3 такие, что Zt = f3'Yt является /(0). Таким образом, может быть больше одного коинтегрирующего вектора (3. Очевидно, что управлять долгосрочным динамическим поведением к переменных могут несколько соотношений равновесия. В общем, может быть г < к — 1 линейно независимых коинтегрирующих векторов п которые собраны в к х г коинтегрирующую матрицу(3. По построению, ранг матрицы13^ (3 равен г, и называется коинтегриру-ющим рангом Yt. Это означает, что каждый элемент в г-мерном векторе Zt = (3'Yt есть /(0), в то время как каждый элемент в /с-мерном векторе Yt есть /(1).

Теорема представления Грэнжера (Engle, Granger, 1987) непосредственно распространяется на этот общий случай и утверждает, что если Yt коинтегрированный, то существует обоснованное представление данных в виде модели коррекции остатков. Хотя существуют различные способы получить и описать такое представление, здесь мы начнем с векторной модели авторегрессии для Yt, введенной в предыдущем параграфе:

Yt = S + 6iU_! + ... + epYt-p + єр (9.42)

или

e{L)Yt = S + et. (9.43) Для случая р — 3 мы можем написать ВАР в виде

AYt = S+ (Єї + 62 -Ik)Yt-! e2AYt-! + e3AYt-s+et =

= 5+ (ві + Є2 + Оз h)Yt-i 02Дй-і 0з(Д£-і + AYt-2) + ?t

или

AYt = S + ГіAYt-г + Г2ДУ*-2 + (0і + 62 + 63 h)Yt-i + eu

Существование к коинтегрирующих соотношений между к элементами в Yt означало бы, что существуют к независимых линейных комбинаций, которые являются /(0), такие, что, обязательно, все индивидуальные элементы в Yt должны быть 1(0). Ясно, что это противоречит определению коинтеграции как свойства переменных /(1), и отсюда следует, что г < к — 1. Мы придерживаемся принятого в литературе по коинтеграции обозначения коинтегрирующей матрицы греческой строчной буквой (3. См. Приложение. А для определения ранга матрицы.

где Гі = —О] 9з и Г2 = — О3. По аналогии в общем случае, т.е. для любого значения р мы можем написать, что14)

AYt = 6 + ГіAft-i + ... + Гр_і AFt-p+i + + ft, (9.44)

где «долгосрочная динамическая матрица»

П = -6(1) = -(4 Єї ... Ор) (9.45)

определяет долгосрочные динамические свойства Yt1^. Это уравнение является прямым обобщением регрессий, применяемых в расширенном тесте Дики—Фуллера. Поскольку AYt и St являются стационарными (по предположению), то вектор ПЇ^-і в соотношении (9.44) должен быть также стационарным. Это может отражать три различные ситуации. Во-первых, если все элементы в Yt интегрируемые порядка один, и никаких коинтегрирующих соотношений не существует, то в этом случае П = 0 и соотношение (9.44) представляет (стационарную) модель ВАР для AYt. Во вторых, если все элементы в Yt являются стационарными переменными /(0), то матрица П = —0(1) должна иметь полный ранг и быть обратимой, так что мы можем написать векторное представление скользящего среднего Yt = —0-1(L)(5 + St). В-третьих, если матрица П имеет ранг г (0 < г < /с), то элементы в векторе ПУ^-і являются линейными комбинациями, которые стационарны. Если переменные в Yt являются /(1), то эти линейные комбинации должны соответствовать коинтегрирующим векторам. Этот промежуточный случай наиболее интересен. Если матрица П имеет редуцированный ранг г < к — 1, то это означает, что существует г независимых линейных комбинаций из к элементов в Yt, которые являются стационарными, то есть: существует г коинтегрирующих соотношений. Заметим еще раз (см. выше сноску 11), что существование к коинтегрирующих соотношений невозможно: если к независимых линейных комбинаций анализируемых к переменных порождают стационарный ряд, то все к переменных сами должны быть стационарными.

Если матрица П имеет редуцированный ранг, то ее можно записать в виде произведения к х г матрицы 7 на г х к матрицу (3',

Возможно переписать ВАР так, что любой из лагов появляется в уровнях в правой части с теми же самыми коэффициентами, что и в «долгосрочной динамической матрице» П. Для сравнения с одномерным случаем мы выбираем включение первого лага.

В одномерном случае долгосрочные динамические свойства определяются 0(1) где 9{L) — полином АР (см. главу 8).

которые обе имеют ранг г 16 Таким образом, П = 7/?'Подстановка этого выражения в соотношение (9.44) порождает модель в форме коррекции остатков

AY = 5 + Гі ДУ*-1 + • • • + Гр_1 Дй-р+і + lPfYt-i + et. (9.46)

Линейные комбинации f3itпредставляют г коинтегрирующих соотношений. Коэффициенты в 7 измеряют, как элементы в AYt корректируются относительно г «остатков равновесия» Zt— (3fYt-i. Таким образом, модель (9.46) является обобщением модели (9.24) и называется векторной моделью коррекции остатков (ВМКО).

Если взять математические ожидания всех членов модели коррекции остатков, то получаем:

(j _ Гі ... ГР^)Е{AYt} = 5 + 7S{Zt_i}. (9.47)

Нет никакого детерминированного тренда в любой из переменных, если E{AYt} — 0. Для того, чтобы согласно предположению, матрица (I — Ті — ... — Гр_і) была невырожденной, требуется, чтобы S + /yE{Zt-i} = 0 (ср. п. 9.2.3), где E{Zt-\] соответствует вектору свободных членов в коинтегрирующих соотношениях. Если мы налагаем это ограничение, то свободные члены появляются только в коинтегрирующих соотношениях. Но мы можем переписать модель коррекции остатков в терминах zt — Zt— E{Zt-i) и тем самым освободиться от всех свободных членов, то есть:

AYt = ГіAYt-! + ... + Гр_іДУ4-р+і + 7(-<* + /^t-i) + <П,

где а — г-мерный вектор констант, удовлетворяющий

Ei/3'Yt^} = E{Zt-i} = а.

В результате все члены в этом выражении имеют нулевое среднее, и никаких детерминированных трендов не существует.

Если мы добавляем одну общую константу к векторной модели коррекции остатков, то мы получаем

AYt = А + Г: AYt-! + ... + Гр_і Дй-р+і + 7(-<* + /^t-i) + eu

Это означает, что г столбцов в 7 линейно независимы, и что г строк в /3' являются независимыми (см. Приложение А).

где А — fc-мерный вектор с идентичными компонентами Ai. Теперь долгосрочное динамическое равновесие соответствует устойчивому состоянию траектории роста с темпами роста для всех переменных, заданных в виде

^{ДУ4} = (/-Г1-...-Гр_1)-1Л.

Предполагается, что детерминированные тренды в каждом Yjt в долгосрочной динамике должны уравновешиваться (т. е. в итоге исчезать), так что никакой детерминированный тренд не будет присутствовать в модели коррекции остатков. Мы можем даже учитывать отдельные к — г детерминированные тренды, которые уравновешиваются в коинтегрирующих соотношениях, в случае когда мы обращаемся к спецификации (9.46) без ограничений на S. При этом 5 включает г свободных членов в долгосрочных динамических соотношениях и к — г различных детерминированных трендов в переменных в Yt. Если есть больше, чем к — г отдельных детерминированных трендов, они не могут уравновеситься в /3lt-l, и мы должны включить детерминированный тренд в коинтегрирующие уравнения. Дополнительное обсуждение и некоторые альтернативы см. у Харриса (Harris, 1995, р. 96).

9.5.2. Пример: коинтеграция в двумерной векторной модели авторегрессии

В качестве примера рассмотрим случай к = 2. В этом случае число коинтегрирующих векторов может быть равным нулю или единице (г = 0, 1). Рассмотрим (нестационарную) модель ВАР первого порядка для Yt = (Yt, Xt)'Таким образом,

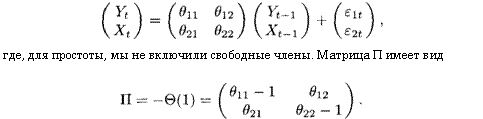Данная матрица является нулевой, если 0П = 022 = 1 и #12 = #21 = О, а значит Yt и Xt — два случайных блуждания. Матрица П имеет редуцированный ранг, если

(011 1)(022 1) #21012 = 0.

(9.48)

В таком случае

/З' = (0П 1 012)

является коинтегрирующий вектором (при условии, что мы выбрали произвольную нормировку), и мы можем написать

П 7/3' =

1

021

(flu -1 М-

011 -1 /

+

+

Yt-i Xt-i

012 022 — 1

є It £2t

011-1

021

Используя эту матрицу, мы можем записать модель в форме коррекции остатков. Сначала напишем

xt) = (x*_i.

Затем перепишем как

(9.49)

є и

£2t

VAX,

fl21 J ((0и ВД-і + 9l2Xt-i) + 011 1 /

Форма коррекции остатков, таким образом, весьма проста, поскольку она исключает любую динамику. Заметим, что как Yt, так и Xt корректируются остатком равновесия, поскольку исключается #21—0. (Также заметим, что #21 = 0 означало бы, что 9ц = #22 = 1 и коин-теграции отсутствует.)

Из этого результата также следует вывод, что линейная комбинация Zt = (9ц — l)Yt + 0i2.Xt является /(0). Заметим, что мы

можем написать

/

021

Zt-1 + (011 1 012)

AZt = (011 1 012)

£2t

V 011 1 /

или (используя условие (9.48)):

Zt = Zt-! + (Єц 1 + 022 l)Zt-l +Щ = (011 + 022 l)Zt-l + Vt

где vt — (0ц — 1)єц + 0i2^2t — остаточный член в форме белого шума. Следовательно, Zt описывается стационарным процессом АР(1),

єсли 0ц ф 1 и 022 ф 1.

9.5.3. Тестирование на коинтеграцию

Если известно, что существует только один коинтегрирующий вектор, то наиболее простым подходом для тестирования существования коинтеграции является подход Энгле—Грэнжера (Engle—Granger), описанный в п. 9.2.3. Этот подход требует построения регрессии Y (переменной, являющейся первым элементом Yt) по другим к—1 переменным >2£, • • • , Ykt и тестирования на наличие единичного корня в МНК-оцененных остатках. Это можно сделать, используя тесты РДФ*) на МНК-оцененных остатках, имея в виду критические значения из таблицы 9.2. Если гипотеза наличия единичного корня отклоняется, то это значит, что отклоняется и гипотеза «отсутствие коинтеграции». В данном случае, статическая регрессия дает состоятельные оценки коинтегрирующего вектора, тогда как на второй стадии можно оценить модель коррекции остатков, используя оцененный коинтегрирующий вектор из первой стадии.

Однако в подходе Энгле—Грэнжера существуют некоторые проблемы. Во-первых, результаты тестов чувствительны к переменной в левой части регрессии, то есть, к нормировке, применяемой к коин-тегрирующему вектору. Во вторых, в случае, если коинтегрирующий вектор, не включает Y^, а только Y^u • • • ? Ykt, тест не приемлем и коинтегрирующий вектор не будет состоятельно оценен регрессией Y по І2£, • • • , YktВ-третьих, возможно, что между переменными Yu, ... , Ykt существует более, чем одно коинтегрирующее соотношение. Если, например, существуют два различных коинтегрирующих соотношения, то обычно МНК оценивает их линейную комбинацию (см. Гамильтон (Hamilton, 1994, р. 590)). К счастью, поскольку нулевая гипотеза для тестов коинтеграции состоит в отсутствии коинтеграции, то тесты все же соответствуют своей цели.

Альтернативный подход без предыдущих недостатков был предложен Иохансеном (Johansen, 1988), который разработал процедуру оценивания максимального правдоподобия, с помощью которой также возможно тестировать число коинтегрирующих соотношений. Детали процедуры Иогансена очень сложны и мы рассмотрим только некоторые аспекты. Более детально с этим подходом можно ознакомиться у Иохансена и Джуселиуса (Johansen, Juselius, 1990) и Иохансена (Johansen, 1991), или в учебниках, таких как Бейнрджи и др. (Banerjee et al, 1993, Глава 8); Гамильтон (Hamilton, 1994, Глава 20); Иохансен (Johansen, 1995, Глава 11) и Стюарт и Гилл (Stewart, Gill, 1998, Разделы 9.4 и 9.5). Отправной точкой процедуры Иохан 

Речь идет о модифицированных РДФ-тестах, использующих критические значения из таблиц, разработанных Дэвидсоном и МакКинноном (примеч. научн. ред. перевода).

сена является представление векторной модели авторегрессии Yt, заданной соотношением (9.44), в виде:

AYt = 5 + Гі ДУ*_і + ... + Гу_! ДУ,_р+1 + ГЩ_! + еи (9.50)

где et является НОНР(0,Т,). Напомним, что применение метода максимального правдоподобия требует, чтобы мы постулировали общий вид закона распределения для элементов белого шума. Предполагая, что Yt является вектором 1(1) переменных, в то время как г линейных комбинаций Yt являются стационарными, мы можем написать

П = 7/3', (9.51)

где, как прежде, 7 и (3 имеют размерность к х г. Снова, (3 обозначает матрицу коинтегрирующих векторов, в то время как 7 представляет матрицу весов, с которыми каждый коинтегрирующий вектор входит в каждое из уравнений AYt. Подход Иохансена основан на оценивании методом максимального правдоподобия системы (9.50), с наложением ограничения (9.51) для заданного значения г.

Первый шаг в подходе Иохансена включает тестирование гипотезы о ранге долгосрочной динамической матрицы П или, что равнозначно, о числе столбцов в (3. При заданном г, можно показать (см., например, Гамильтон (Hamilton, 1994, Sect. 20.2)), что оценка максимального правдоподобия для /3 равняется матрице, содержащей г собственных векторов, соответствующих г наибольшим (оцененным) собственным значениям кхк матрицы, которую можно легко оценить, используя программы, реализующие МНК. Обозначим (теоретические) собственные значения этой матрицы в порядке убывания: Аі > Л2 > ... > Хк. Если существуют г коинтегрирующих соотношений (и П имеет ранг г), то для к — г наименьших собственных значений j=r + l,r + 2,...,fc должно иметь место log (1 — Xj) = 0. Мы можем использовать оцененные собственные значения, скажем Ai>A2>...>Afc, чтобы протестировать гипотезы о ранге П. Например, гипотезу Hq : г < го против альтернативной гипотезы Ні : Го < г < к можно протестировать, используя статистику

к

Atrace(ro) = -Т J2 log (1-АД (9.52)

j=r0 + l

Это так называемый тест следа. С его помощью проверяется, отличаются ли значимо от нуля к — го наименьших собственных значений. Кроме того, мы можем протестировать Hq : г < г о против более

ограниченной альтернативной гипотезы Hi : г — го + 1, используя Amax(ro) -Г log (1 АГо+1). (9.53)

Этот альтернативный тест называется тестом максимального собственного значения, поскольку он основан на оцененном (го + 1)-ом наибольшем собственном значении.

Два описанных здесь теста, фактически, являются тестами отношения правдоподобия (см. главу 6), но не имеют обычных распределений хи-квадрат. Вместо этого соответствующие распределения являются многомерными расширениями распределений Дики— Фуллера. Как и в случае с тестами наличия единичного корня, процентили распределений зависят от факта наличия константы (и временного тренда). Критические значения для этих двух случаев представлены в таблице 9.9. Случай 1 предполагает, что нет никаких детерминированных трендов, и включает г свободных членов в коинтегрирующие соотношения. Случай 2 основан на включении к свободных членов в ВАР (без ограничений), которые подразумевает наличие к —г отдельных детерминированных трендов и г свободных членов в векторах коинтеграции. Критические значения зависят от к — го, числа нестационарных компонентов при нулевой гипотезе. Заметим, что, когда к — г о = 1, эти две критические статистики идентичны и таким образом имеют одно и то же распределение.

Важно понимать, что параметры 7 и (3 идентифицируются не однозначно, в том смысле, что различные комбинации 7 и (3 могут порождать одну и ту же матрицу П = 7/3'. Это потому, что 7/?' = 7РР-1/3/ для любой обратимой г х г матрицы Р. Другими словами, данные могут определить пространство, натянутое на столбцы /3, пространство коинтеграции, и пространство, натянутое на 7. Следовательно, коинтегрирующие векторы в (3 должны нормироваться некоторым образом, чтобы получились однозначные коинтегрирующие соотношения. Часто надеются, что эти соотношения могут иметь разумную экономическую интерпретацию.