10.7.3. оценивание с неслучайно пропущенными данными

10.7.3. оценивание с неслучайно пропущенными данными

Как и в пространственном ("cross-sectional") случае (см. параграф 7.5) смещение из-за пропущенных данных порождает проблему идентификации. В результате при наличии смещения из-за пропущенных данных, если не наложить дополнительные предположения, состоятельное оценивание параметров модели невозможно. В качестве примера предположим, что индикатор пропущенных данных Гц можно объяснить пробит-моделью со случайными эффектами, то есть,

4=47 + & + \%, (10-93)

где Гц — 1, если Гц > 0 и Гц = 0 в противном случае, a zu — (хорошо-мотивированный) вектор экзогенных переменных, который включает хц. Интересующая нас модель задается в виде

yit = x'itf3 + oti + ец. (10.94)

Предположим, что компоненты остатков модели в этих двух уравнениях имеют совместное нормальное распределение. Тем самым приходим к обобщению пространственной выборочной модели с пропущенными данными, которая рассматривалась в п. 7.4.1. Влияние ограничений на формирование выборки для модели (10.94) отражается в математических ожиданиях ее ненаблюдаемых компонентов, условных по экзогенным переменным и индикаторам пропуска, то есть

E{oLizn,..., ziT, Гц,..., riT} (10.95)

и

E{eitziU ziT, riU..., riT}. (10.96)

Можно показать (Verbeek и Nijrnan, 1992), что условное математическое ожидание (10.96) не зависит от времени, если cov {єц, г)ц} = 0,

' Предложенный здесь тест реально не является тестом Хаусмана, поскольку при альтернативной гипотезе ни одна из оценок не является состоятельной. Тем не менее, тест, сам по себе, является корректным; просто, при применении в определенных обстоятельствах он может характеризоваться ограниченной мощностью.

или если 2:^7 не зависит от времени. Это требуется для состоятельности оценок с фиксированными эффектами. Далее, условное математическое ожидание (10.95) равно нулю, если cov {с^, £;} = 0, тогда как условное математическое ожидание (10.96) равно нулю, если cov {ей, r)it} = 0, так что оценка со случайными эффектами состоятельна, если ненаблюдаемые переменные в основном уравнении (10.94) и в уравнении для индикатора пропуска (10.93) некоррели-рованы.

В общем случае оценивание относительно более сложное. В статье (Hausman, Wise, 1979) рассматривается случай, когда панельные данные включают два такта времени, и пропущенные наблюдения имеют место только на втором такте. В более общем случае применение метода максимального правдоподобия для одновременного оценивания этих двух уравнений требует численного интегрирования в пространстве размерности выше двух (чтобы с помощью интегрирования исключить эти два индивидуальных эффекта). В статьях (Nijman, Verbeek, 1992) и (Vella, Verbeek, 1999) представлены альтернативные оценки, основанные на двухшаговом методе оценивания для пространственной выборочной модели с пропущенными данными. По существу, идея состоит в том, что члены в условных математических ожиданиях (10.95) и (10.96), кроме константы, можно определить из пробит-модели (10.93), так что оценки этих членов могут включаться в основное уравнение. В статье (Wooldridge, 1995) представлены некоторые альтернативные оценки на основе несколько других предположений.

Упражнения

Упражнение 10.1 (линейная модель)

Рассмотрим следующую простую модель панельных данных

Ун = Хіф + a* + eiu і = 1,..., N, t = 1,..., Г, (10.97)

в которой /3 — одномерный неизвестный параметр, и предполагается, что

а*=Хг + а{ с ai~HOHP(0,al), eit ~ #О#Р(0, а£2), взаимно независимыми, и независимыми от всех хц, где

Параметр (3 в модели (10.97) можно оценить с помощью оценки с фиксированными эффектами (или с помощью внутригрупповой оценки), заданной в виде

N Т

J2J2(Xit -^){Угі -Уі)

N Т

i=i t=i

Как альтернатива, корреляция между остатком а* + вц и переменной хц может быть учтена с помощью применения метода инструментальных переменных.

а. Приведите выражение для МИП-оценки (Зип параметра /3 в

модели панельных данных (10.97), используя в качестве инструментальной переменной для хц переменную хц — Хі . Покажите,

что (Зип и 0фэ идентичны.

Другой способ исключать индивидуальные эффекты а* из модели состоит во взятии первых разностей. В результате приходим к выражению

Уа Уі,г-1 = {хц Xi,t-l)(3 + (єа Єг,*-і),

(10.98)

г = 1,...,ЛГ, І = 1,...,Г.

б. Обозначьте МНК-оценку, основанную на модели первых разностей (ПР) (10.98), через (ЗпрПокажите, что оценка (Зпр идентична оценкам (Зип и /Зфэ, если Г = 2. Эта идентичность для

Г > 2 больше не справедлива. В таком случае какую из этих

двух оценок Вы бы предпочли? Объясните. (Примечание: для

дополнительного обсуждения см. (Verbeek, 1995).)

в. Рассмотрите межгрупповую оценку (Зм параметра (3 в модели

(10.97). Дайте выражение для оценки (Зм и покажите, что она

является несмещенной для векторного параметра (3 + А.

г. И, наконец, предположите, что мы подставляем выражение для

а* в модель (10.97) и получаем

yit = x'it(3 + х{ + а{ + ец, і = 1,..., N, t = 1,..., Г. (10.99)

Вектор (/З, А)' можно оценить с помощью ОМНК (случайные эффекты) из модели (10.99). Можно показать, что полученная таким образом оценка параметра /3 идентична оценке РфэОзначает ли это, что никакого реального различия между подходами случайных и фиксированных эффектов нет? Примечание: для дополнительного обсуждения см. (Hsiao, 1986, Sect. 3.4.2а.)

Упражнение 10.2 (модель Хаусмана—Тейлора)

Рассмотрим следующую линейную модель панельных данных

Vlt = x'hitPi + X'2it(32 + + ^2,г72 + «і + Єіи (10.100)

в которой Wk,i не зависит от времени, a Xk,u, являются объясняющими переменными, изменяющимися во времени. Переменные с индексом 1 (#і,гг и W\^) строго экзогенны в том смысле, что E{xjtOLi} = 0, Е{хііі8єц} = 0 для всех s и £, E{wjOLi} = 0 и E{wi^6it} — 0. Также предполагается, что Е{и)2,іЄц} — 0, и что выполняются обычные условия регулярности (обеспечивающие состоятельность и асимптотическую нормальность).

а. При каких дополнительных предположениях, МНК, примененный к модели (10.100), обеспечивает состоятельную оценку для

векторов параметров р = (/?i, fa)' и 7 = (7ъ 72)'?

б. Рассмотрите (внутригрупповую) оценку с фиксированными эффектами. При каких дополнительных предположениях она являлась бы состоятельной оценкой для вектора параметров ft?

в. Рассмотрите МНК-оценку для вектора параметров Р на основе

регрессии в первых разностях. При каком (каких) дополнительном предположении (ях) эта оценка является состоятельной для

вектора параметров Р?

г. Обсудите одну или более альтернативных состоятельных оценок для векторов параметров Р и 7 при предположениях:

E{x2,is£it} — 0 (для всех s и £), и E{w2,iSu} = 0. Каковы

ограничения в этом случае на число переменных в каждой из

категорий?

д. Обсудите оценивание вектора параметров /3, если Х2,ц равняется Vi,t-l.

е. Обсудите оценивание вектора параметров /3, если Х2,ц включает

Vi,t-iж. Можно ли оценить состоятельно, как вектор параметров /3, так и вектор параметров 7, если #2,it включает y^t-i? Если можно, то как? В противном случае, почему нет? (В случае необходимости сделайте дополнительные предположения.)

Упражнение 10.3

(динамические модели и модели бинарного выбора)

Рассмотрим следующее динамическое уравнение заработной платы

wit = x'itf5 + jWi^t-i + oti + eit, (10.101)

где wu обозначает логарифм почасовой ставки заработной платы индивидуума, а хи — вектор персональных характеристик и характеристик работы (возраст, время обучения, пол, отрасль промышленности, и т. д.).

а. Объясните на словах, почему МНК, примененный к модели

(10.101), является несостоятельным.

б. Объясните также, почему оценка с фиксированными эффектами, примененная к модели (10.101), является несостоятельной

при N —► ос и фиксированном Г, но состоятельная при N —> оо

и Г —» оо. (Предположите, что остатки Ец являются независимо

и одинаково распределенными.)

в. Объясните, почему результаты из пунктов а и б также означают, что оценка со случайными эффектами (ОМНК-оценка) для

модели (10.101) будет несостоятельной и при фиксированном Г.

г. Опишите простую состоятельную (при N оо) оценку для вектора параметров (3 и параметра 7, предполагая, что осі и Ец

являются независимо и одинаково распределенными и независимыми от всех Хц .

д. Опишите более эффективную оценку для вектора параметров /3

и параметра 7 при тех же самых предположениях.

В дополнение к уравнению заработной платы предположим, что существует модель бинарного выбора, объясняющая, работает индивидуум или нет. Пусть гu = 1, если индивидуум і работал в такте времени £, и Гц = 0 в противном случае. Тогда модель можно написать как

ru = Zits + €i + Vit,

vu 1, если r*t > 0, (10.102)

гu = 0 в противном случае.

где zu — вектор персональных характеристик. Предположим что £і ~ НОНР(0, <т|) и rjit ~ НОНР(0,1 — о-|), взаимно независимы и независимы от всех гц. Модель (10.102) можно оценить методом максимального правдоподобия.

е. Дайте выражение для вероятности того, что Гц — 1, при заданных Zit И & •

ж. Используйте выражение из пункта е, чтобы получить выражение вклада индивидуума і в правдоподобие, легко поддающееся обработке в вычислительном отношении.

з. Объясните, почему невозможно рассмотреть эффекты как

фиксированные неизвестные параметры и оценить 6 состоятельно (при фиксированном Г) из пробит-модели с фиксированными

эффектами?

С этого момента предположим, что соответствующее уравнение заработной платы является статическим и задается выражением (10.101) с параметром 7 = 0.

и. Каковы последствия для оценки со случайными эффектами

модели (10.101), если гін и ец коррелированны? Почему?

к. Каковы последствия для оценки с фиксированными эффектами модели (10.101), если & и щ коррелированны (в то время как rjit и eit нет)? Почему?

А

Векторы и матрицы

Периодически в этом тексте используются понятия и результаты линейной алгебры. Это приложение предназначено для краткого изложения этих понятий и результатов. Более детальное описание можно найти в учебниках по линейной алгебре или, например, в главе 2 книги (Greene, 2000) или в приложении А книги (Davidson, MacKinnon, 1993). Здесь представлены и относительно сложные темы, которые использовались в ограниченном числе мест в тексте. Например, собственные значения и ранг матрицы встречаются только в главе 9, в то время как правила дифференцирования необходимы только в главах 2 и 5.

А.1. Терминология

В этой книге вектор всегда является вектором-столбцом чисел, обозначаемым

/аі

«2

а —

ап/

Транспонирование вектора, обозначаемое о! — (ai, a2,... , an), является строкой чисел, иногда называемой вектором-строкой. Матрица — это прямоугольная таблица чисел. Для размерности п х к

ее можно написать как

А =

( ац

«21

ai2

CL22

0>1п &2n

Первый подстрочный индекс элемента обозначает номер строки, а второй подстрочный индекс — номер столбца. Обозначая j-ый столбец этой матрицы через aj, можно сказать, что матрица А состоит из к вектор-столбцов от ai до а/с, которые мы можем обозначить как

A=[ai a2 ... ak}.

Символ ' обозначает транспонирование матрицы или вектора, приводящее к виду

/ ац а2і ... ani

аі2 а22 аП2

о>к ... ank/

Столбцы матрицы А являются строками транспонированной матрицы А' и наоборот. Матрица является квадратной, если п = к. Квадратная матрица А является симметрической, если А — А!. Квадратную матрицу А называют диагональной матрицей, если aij = 0 для всех і ф j. Отметим, что диагональная матрица является симметрической по построению. Единичная матрица / — это диагональная матрица со всеми диагональными элементами, равными единице.

А.2. Действия с матрицами

Если две матрицы или два вектора имеют одинаковые размерности, то их можно складывать или вычитать. Пусть А и В — две матрицы размерности п х к с элементами а^ и > соответственно. Тогда матрица А + В состоит из элементов а^ + bij, в то время как матрица А — В состоит из элементов а^ — . Отсюда легко следует, что А + В = В + А и (А + В)' = А' + В'.

Матрицу А размерности пхк можно умножить на матрицу В размерности к х т, тогда получим матрицу размерности п х т.

Сначала рассмотрим специальный случай к = 1. Тогда А — о! есть вектор-строка, а В = Ь — вектор столбец. И мы определяем

/Ьі

АВ = a'b = (ai, a2,... , an)

= aibi + a2?>2 + • • • + anbn-

Мы называем произведение a'b скалярным произведением векторов а и Ъ. Отметим, что a'b = b'a. Два вектора называются ортогональными, если a'b = 0. Для любого вектора а* кроме нулевого вектора, имеем, что а'а > 0. Внешнее произведение а есть aa;, которое имеет размерность п х п.

Другой частный случай возникает для m — 1, когда А — п х к матрица, а В = Ъ — вектор размерности к. Тогда с = А В также является вектором, но размерности п. Его элементами являются элементы

Сі = ацЬі + аі2Ь2 + ... + dikbk,

которые является скалярным произведением вектора, полученного из г-ой строки матрицы А и вектора Ъ.

Если m > 1, то В является матрицей, и С = АВ — матрица размерности п х m с элементами

Cfj = anbij + ai2b2j + ... + dikbkj,

являющимися скалярными произведениями между векторами, полученными из г-ой строки матрицы А и j-ro столбца матрицы В. Отметим, что это может иметь смысл, если только число столбцов в матрице А равняется числу строк в матрице В. В качестве примера рассмотрим

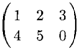
А =

	(1	2
в =	3	4
	1°	5

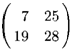
АВ =

С действительными компонентами (примеч. научн. ред. перевода).

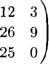
Важно отметить, что АВ ф В А. Даже если матрица АВ существует, то матрица В А может быть не определена, поскольку размерности В и А не соответствуют. Если матрица А имеет размерность п х к, а матрица В имеет размерность к х п, то матрица АВ существует и имеет размерность п х п, в то время как матрица В А существует с размерностью к х к. В вышеприведенном примере мы имеем

( 9

ВА= 19

Для транспонирования произведения двух матриц справедливо, что

{АВУ = В'А'.

Из этого (и (А')' — А) следует, что матрицы А'А и AAf существуют и они симметрические. И, наконец, элементы матрицы сА произведения скаляра с и матрицы А равны произведению каждого элемента матрицы А на этот скаляр с. Таким образом, для скаляра с мы имеем, что матрица с А имеет элемент са^.

А.З. Свойства векторов и матриц

Если мы рассматриваем ряд векторов от вектора а до ак, то мы можем построить линейную комбинацию этих векторов. Со скалярными весами С,... , Ck линейная комбинация порождает вектор

са + C2d2 + ... + с/сзд,

который мы можем кратко записать как Ас, где, как и прежде, A=[ai а2 ... ак] и с = (сь ... , ск)'.

Множество векторов линейно зависимо, если любой из векторов можно записать в виде линейной комбинации других векторов. То есть, если существуют значения сі,... , с^, не все равные нулю, так что

CGL + C2CL2 + . . . + Ckdk = о

(нулевой вектор). Эквивалентно, множество векторов линейно независимо, если единственное решение уравнения

CCL + С2СІ2 + . . . + CkCLk = о

относительно скалярных весов С

Ck равно

с = с2 = ... = ск = 0.

То есть, если единственное решение для Ас = 0 есть с = 0.

Если мы рассмотрим все возможные векторы, которые можно получить как линейные комбинации векторов ai, a2,... , а/-, то эти векторы образуют векторное пространство. Если векторы, ai, a2,... , а/с линейно зависимы, то мы можем уменьшить число векторов, не изменяя векторное пространство. Минимальное число векторов необходимое, чтобы натянуть векторное пространство, называется размерностью этого пространства. Таким способом мы можем определить пространство столбцов матрицы как пространство, натянутое на ее столбцы, а ранг столбцов матрицы — как размерность ее пространство столбцов. Ясно, что ранг столбцов никогда не может превышать число столбцов. Матрица имеет полный ранг столбцов, если ранг столбцов равняется числу столбцов. Ранг строк матрицы — размерность пространства, натянутого на строки матрицы. В общем, справедливо, что ранг строк и ранг столбцов матрицы равны, и, таким образом, мы можем однозначно определить ранг матрицы. Отметим, это не означает, что матрица, которая имеет полный ранг столбцов, имеет автоматически полный ранг строк (это справедливо, если только матрица квадратная). Полезный результат в регрессионном анализе состоит в том, что для любой матрицы А

rank (А) = rank [А!'А) = rank (АА').

А.4. Обратные матрицы

Например,

122

V

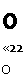
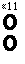
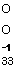
О

v 0

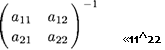a

И

&22 -&21

«12^21

Если ацй22 — &12&21 = О, то 2 х 2 матрица А вырождена: ее столбцы линейно-зависимы, и также линейно зависимы ее строки. Мы называем аца22 — &і2а2і определителем этой 2x2 матрицы (см. ниже).

Предположим, что нас просят решить матричное уравнение Ac — d для заданных матрицы А и вектора d, где матрица А имеет размерность пхп, асис!n-мерные векторы. Такое матричное уравнение является системой из п линейных уравнений с п неизвестными. Если обратная матрица А~1 существует, то мы можем написать

А~1Ас — с — A~ld,

чтобы получить решение. Если матрица А необратима, тогда система линейных уравнений имеет линейные зависимости. Есть две возможности. Либо решению системы уравнений (матричного уравнения) Ас — d удовлетворяет более чем один вектор с, и тогда единственного решения не существует; либо уравнения несовместны, и тогда решение системы не существует совсем. Если d — нулевой вектор, то остается только первая возможность. Непосредственно получается, что

И

(АВ)

-1

В~1А~

(предполагая, что обе обратные матрицы существуют).

А. 5. Идемпотентные матрицы

Специальный класс матриц — класс симметрических и идемпотент-ных матриц. Матрица Р является симметрической, если Р1 — Р, и идемпотентной, если РР = Р. Симметрическая идемпотентная матрица Р имеет интерпретацию проекционной матрицы. Это

означает, что вектор проектирования Рх находится в пространстве столбцов матрицы Р, в то время как остаточный вектор х — Рх ортогонален к любому вектору в пространстве столбцов матрицы Р.

Проекционную матрицу, которая проецирует на пространство столбцов матрицы А можно построить как Р — A(AfА)~хА'. Ясно, что эта матрица является симметрической и идемпотентной. Проецирование дважды на одно и то же пространство должно оставлять результат неизменным, и таким образом, мы должны иметь соотношение РРх = Рх, которое следует непосредственно. Остаток от проецирования есть х — Рх — (I — А(А'А)~хА')х, так что М — I — А(А'А)~хАг также является проекционной матрицей с MP = РМ = 0 и ММ = М = М'. Таким образом векторы Мх и Рх ортогональны.

Интересная проекционная матрица (которая используется в главе 10) — это Q — I — (1/п)и;, где і — n-мерный вектор единиц (так что о! является матрицей единиц). Диагональные элементы в этой матрице равны 1 — 1/п. а все не диагональные элементы равны — 1/п. Тогда Qx является вектором, содержащим отклонения х от своего среднего значения. Вектор средних значений порождается матрицей преобразования Р = (1/п) а7. Отметим, что РР = Ри QP = 0.

Единственной невырожденной проекционной матрицей является единичная матрица. Все другие проекционные матрицы вы-рожденны, каждая имеет ранг равный размерности пространства, на которое они проектируют.

А.6. Собственные значения и собственные векторы

Пусть А — будет п х п симметрической матрицей. Рассмотрим следующую проблему поиска комбинаций вектора с (кроме нулевого вектора) и скаляра Л, которые удовлетворяют

Ас = Лс.

В общем, существует п решений А,... , Ап, называемых собственными значениями (характеристическими корнями) матрицы А, соответствующих п векторам с, ... , сп, называемых собственными векторами (характеристическими векторами). Если с является решением, тогда, кс для любой константы к тоже является собственным, вектором, поэтому собственные векторы определены с точностью до константы. Собственные векторы симметрической матрицы ортогональны, то есть c[cj = 0 для всех г ф j.

Если собственное значение равно нулю, соответствующий вектор с удовлетворяет Ас = О, тогда подразумевается, что матрица А неполного ранга, и, следовательно, вырождена. Таким образом, вырожденная матрица имеет, по крайней мере, одно нулевое собственное значение. В общем, ранг симметрической матрицы соответствует числу ненулевых собственных значений.

Симметрическую матрицу называют положительно определенной, если все ее собственные значения положительны. Ее называют положительно полуопределенной, если все ее собственные значения неотрицательны. Положительно определенная матрица обратима. Если матрица А положительно определенная, то для любого вектора х (не нулевого вектора) справедливо, что

х'Ах > 0*}.

Причина состоит в том, что любой вектор х можно написать в виде линейной комбинации собственных векторов как

х = dc + ... + dncn

для скаляров d,... , dn, и мы можем написать

XіАх = {dc + ... + (1пСпУA(dici + ... + dncn) = = \dcc + ... + dnc'ncn > 0.

Точно так же для положительно полуопределенной матрицы А мы имеем, что для любого вектора х

х'Ах > 0*}.

Определитель симметрической матрицы равен произведению ее п собственных значений. Определитель положительной определенной матрицы положителен. Симметрическая матрица вырождена, если определитель равен нулю (то есть, если одно из собственных значений равно нулю).

Верно и обратное утверждение, поэтому это свойство используется также и как определение положительной (неотрицательной) определенности матрицы (примеч. научн. ред. перевода).

А.7. Дифференцирование

Пусть х будет n-мерным вектор-столбцом. Если с также является n-мерным вектор-столбцом, с'х является скаляром. Рассмотрим с'х как функцию от вектора х. Тогда мы можем рассмотреть вектор производных с'х относительно каждого элемента в векторе х, то есть

дс'х дх

Вектор производных является вектор-столбцом из п производных и типичный элемент равен с*. Более обще, для векторной функции Ах (где А — матрица) мы имеем, что

дАх , дх

Элемент в столбце г, строке j этой матрицы является производной j-ro элемента функции Ах относительно Х{. Далее, для симметрической матрицы А

дх'Ах Л А —— = 2Ах. ох

Если матрица А не является симметрической, то мы имеем

дх jA.x , . * і

Все эти результаты следуют из результатов поэлементного дифференцирования.

А.8. Некоторые матричные действия, связанные с методом наименьших квадратов

Пусть Хі = {хц,Хі2, .. • , хІК)' с Хц = 1 и (3 = (/5Ь /?2, • • •, Рк)'Тогда

x • = Рі+ Р2ХІ2 + . . . + РкХіКМатрица

/ Хц

хіх'і =

N

Xi2

(хц,Хі2, . . . , Хік) =

1=1

1=1

ХіК/

1=1

N

г=1 N

1=1

N

г=1

N

N

V г=1

г=1

/

является КхК симметрической матрицей, содержащей суммы квадратов и перекрестных произведений. Вектор

/"

г=1 N

N

У2 ХЯУ*

1=1

i=l

N

г=1 /

имеет длину К, так что система

N ч N

YXiX'i)b = YlXiyi

кі=1 ' г=1

является системой К уравнений с К неизвестными (в векторе Ъ).

N

Если матрица Хіх обратима, то существует единственное решег=1

N

ние. Обращение требует, чтобы матрица ^Г^ Хіх[ была полного ранга.

і=1

Если она неполного ранга, то существует ненулевой К-мерный вектор с такой, что х'гс = 0 для каждого г и существует линейная

N

зависимость между столбцами/строками матрицы ^ Хіх.

г=1

В матричной системе обозначений N х К матрица X определяется как

/ Хц Xi2 ... ХК

Х= : : •. :

Хт XN2 .-. XNK/

и у = (уі, у2, • •. 5 Улг)'• Отсюда легко проверить, что

N

х'х = ]Г

г=1

и

N

і=1

Матрица X'X не является обратимой, если матрица X неполного ранга. То есть, если между столбцами матрицы X («регрессорами») существует линейная зависимость.

в

Теория статистики и теория распределений

В этом приложении кратко рассматриваются основы теории статистики и теории распределений, которые используется в этом тексте. Подробности можно найти, например, в книге (Greene, 2000, Chapter 3) или (Davidson, MacKinnon, 1993, Appendix В).

B.1. Дискретные случайные переменные

Случайная переменная — это переменная, которая может принимать различные значения (исходы) в зависимости от «состояния природы». Например, исход одного броска игральной кости случаен, с возможными исходами 1, 2, 3, 4, 5, и 6. Обозначим произвольную случайную переменную через Y. Если Y обозначает исход эксперимента игры в кости (а кость предполагается честной, т. е. симметричной), вероятность каждого исхода равна 1/6. Мы можем обозначить ее как

Р{У = у} = для г/= 1,2,...,6.

Функция, которая связывает возможные исходы (в этом случае у = 1,2,...,6) с соответствующими вероятностями, называется

В. 2. Непрерывные случайные переменные

579

функцией вероятностной меры или, более обще, функцией, задающей закон распределения вероятностей. Мы можем обозначить ее как

f(y) = P{Y = у}.

Отметим, что f(y) не является функцией случайной переменной У, а является функцией от всех ее возможных исходов.

Функция /(у) имеет свойство, что, если мы просуммируем ее по всем возможным исходам, то в результате получим единицу. То есть

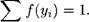
Математическое ожидание дискретной случайной переменной равно взвешенному среднему всех возможных исходов, где веса соответствуют вероятностям отдельных исходов. Мы обозначаем

E{Y} = Y,Vif(yi) 

Отметим, что E{Y} не обязательно соответствует одному из возможных исходов. Например, в эксперименте с игрой в кости математическое ожидание равно 3,5.

Распределение является вырожденным, если оно сосредоточено только в одной точке, то есть, если P{Y — у} = 1 для одного отдельного значения у и P{Y = у} = 0 для всех других значений.

В.2. Непрерывные случайные переменные

На графике вероятность P{a < Y < b} равна площади под функцией f(y) между точками а и Ь. Взяв интеграл от функции /(у) по всем

Непрерывная случайная переменная может принимать бесконечное число различных исходов, например, любое значение в интервале [0,1]. В этом случае каждый отдельный исход имеет нулевую вероятность. Вместо функции вероятностной меры, мы определим функцию плотности вероятностей /(у) > 0 как возможным исходам, получим

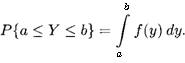оо

J f{y)dy = .

— оо

Если случайная переменная Y принимает значения только в пределах определенного интервала, то неявно предполагается, что функция /(у) = 0 везде вне этого интервала.

Мы также можем определить кумулятивную функцию плотности (кфп) как*)

у

F(y) = P{Y<y}= J f(t)dt,

— оо

так что f(y) = F'(y) (производной). Кумулятивная функция плотности имеет такое свойство, что 0 < F{y) < 1, и является монотонно возрастающей функцией, то есть

F(y) > f(x), если у > х.

Из этого легко следует, что P{a < Y < b} = F(b) — F(a).

Математическое ожидание или среднее значение непрерывной случайной переменной, часто обозначаемое /і, определяется в виде

оо

» = E{Y}= J yf(y)dy.

— оо

Другой мерой положения является медиана, которая является значением m, для которого мы имеем

P{Y<m}>± и Р{у<т}<1-.

Таким образом, 50\% наблюдений располагается ниже медианы, а 50\% наблюдений — выше. Мода — это просто значение у, для которого функция f(y) принимает свое максимальное значение. Она нечасто используется в эконометрических приложениях.

Распределение является симметрическим относительно своего среднего значения, если f(fi — y) — /(// + у). В этом случае среднее значение и медиана распределения идентичны.

Широко распространено также определение функции F(y) как функции распределения вероятностей (примеч. научн. ред. перевода).

В.З. Математическое ожидание и моменты

Если Y и X — случайные переменные, а а и Ъ — константы, тогда справедливо, соотношение

E{aY + 6Х} = aE{Y} + 6£{Х},

которое показывает, что математическое ожидание является линейным оператором. Аналогичные результаты необязательно справедливы, если мы рассматриваем нелинейное преобразование случайной переменной. Для нелинейной функции д, в общем, не справедливо, что E{g(Y)} = g(E{Y}). Если д является вогнутой функцией, то неравенство Иенсена говорит, что

E{g(Y)} < g(E{Y}).

Например, E{og (Y)} < log E{Y}. Отсюда вытекает следствие, что мы не можем определить математическое ожидание функции от случайной переменной Y только из математического ожидания Y. Конечно, по определению справедливо, что

оо

Е{д(У)}= j g(Y)f(Y)dy.

— оо

Дисперсия случайной переменной, часто обозначаемая а2, является мерой разброса распределения. Она определяется как

a2 = V{Y} = E{(Y-tf}

и равняется математическому ожиданию квадрата отклонения от среднего значения. Ее иногда называют вторым центральным моментом. Полезным результатом является соотношение

E{(Y fi)2} = E{Y2} 2E{Y}fi + fi2 = E{Y2} /Д

где E{Y2} — второй момент. Если случайная переменная Y имеет дискретное распределение, то его дисперсия определяется как

v{Y} = j2(Y-rff(y^

г

где і индексирует различные исходы. Для непрерывного распределения мы имеем

оо

V{Y}= J (y-»)2f(y)dy.

— оо

Используя эти определения, легко проверить, что

V{aY + b} = a2V{Y},

где а и Ь — произвольные константы. Часто мы будем также использовать среднеквадратичное (стандартное) отклонение случайной переменной, обозначаемое сг, определяемое как квадратный корень из дисперсии. Среднеквадратичное отклонение выражается в тех же самых единицах, что и случайная переменная Y.

В большинстве случаев распределение случайной переменной не описывается полностью только ее средним значением и дисперсией, и мы можем определить fc-ый центральный момент в виде

Е{(¥-ц)к}, fe = 1,2,3,... .

В частности, третий центральный момент является мерой асимметрии, нулевое значение которого указывает на симметричное распределение, и четвертый центральный момент измеряет эксцесс. Он является мерой тяжести «хвостов» распределения.

В.4. Многомерные распределения

Функция совместной плотности двух случайных переменных Y и X, обозначаемая /(у, х), определяется в виде

Ь ь2

P{ai < У < 6i, a2 < X < b2} = J J f(x, y) dy dx.

Если Y и X независимы, то справедливо соотношение

f(y,x) = f(y)f(x),

так что

P{ai < Y < Ьь a2 < X < Ъ2} = Р{аг < Y < b1}P{a2 < X < Ь2}.

В общем, частное (маргинальное) распределение случайной переменной Y характеризуется функцией плотности

оо

ш = /

f(y, х) dx.

Это подразумевает, что математическое ожидание Y имеет вид

оо оо оо

E{Y}= J yf(y)dy = J j yf(y,x)dxdy.

— oo —oo —oo

Ковариация между случайными переменными Y и X является мерой линейной зависимости между этими двумя переменными. Она определяется как

axy = cov {У, X} = E{(Y ^)(Х //*)},

где Цу = E{Y} и цх = Е{Х}. Коэффициент корреляции задается в виде ковариации, стандартизированной двумя среднеквадратичными отклонениями, то есть,

_ cov {У, X} _ аху

Руа

y/V{Y}V{X} °х°у

Коэффициент корреляции всегда лежит между —1 и 1, и не зависит от масштаба переменных. Если ковариация cov {У, X} = 0, то говорят, что случайные переменные Y и X — некоррелированны. Если а, 6, с, d — константы, то справедливо, что

cov {aY + Ь,сХ + d} = ас cov {У, X}.

Кроме того,

cov {aY + ЪХ, Х} = а cov {У, X} + b cov {X, X} = = acov {Y, X} + bcov {X}.

Из этого также следует, две случайные переменные Y и X коррелированны полностью (рух = 1), если Y = аХ для некоторого ненулевого значения а. Если переменные Y и X коррелированны, то дисперсия линейной функции от переменных Y и X зависит от их ковариации. В частности,

V{aY + ЪХ} = a2V{Y} + b2V{X] + 2ab cov {Г, X}.

Если мы рассматриваем if-мерный вектор случайных переменных Y — (Yi,..., Yk)', то мы можем определить его вектор математических ожиданий в виде

E{Y} =

E{Yk}J

а его дисперсионно-ковариационную матрицу дисперсии (или просто ковариационную матрицу) как

( V{YX}

V{YltYK}

V{Y} =

V{YK,YX}

V{YK} J

Отметим, что эта матрица является симметрической. Если мы рассматриваем одну или более линейных комбинаций элементов в У, скажем ДУ, где R имеет размерность J х К, то справедливо, что

V{RY} = RV{Y}R'.

В.5. Условные распределения

Условное распределение описывает распределение случайной переменной, скажем, У, при заданном условии на значения другой случайной переменной X. Например, если мы бросаем две игральные кости, то переменная X могла бы обозначать исход первой игральной кости, и переменная У могла бы обозначать исход суммы этих двух игральных костей. Тогда мы могли бы интересоваться распределением переменной У, условным по исходу первой игральной кости. Например, чему равна вероятность броска с исходом суммы, равной 7, если первая игральная кость имела исход, равный 3. Или исход 3 и меньше? Условное распределение следует из совместного распределения анализируемых двух переменных. Мы определяем

f(yX = x)=f(yx) = l^.

/0*0

Если случайные переменные У и X независимы, то из этого непосредственно следует, что f(yx) = /(у). Из определения, данного выше, следует соотношение

/(у, я) = f(yx)f(x),

которое говорит, что совместное распределение двух случайных переменных можно разложить на произведение условного и частного (маргинального) распределения. Аналогично мы можем написать

f(y,x) = f(yx)f(y),

Условное математическое ожидание случайной переменной Y для данного значения переменной X — х является математическим ожиданием условного распределения Y. То есть,

E{YX = х} = J yf(yx) dy.

Условное математическое ожидание является функцией х, если только переменные Y и X не являются независимыми.

Аналогично мы можем определить условную дисперсию как

V{Yx} = J(y-E{Yx})2f(yx)dy, которую можно написать в виде

V{Yx} = E{Y2x} (E{Yx})2.

Справедливо, что

V{Y} = EX{V{YX}} + VX{E{YX}},

где Ex и Vx обозначают математическое ожидание и дисперсию,

соответственно, на основе маргинального распределения переменной X. Члены и £{Y|X} являются функциями случайной

переменной X и поэтому эти члены сами являются случайными

переменными.

Рассмотрим соотношение между двумя случайными переменными Y и X, где E{Y} — 0. Тогда отсюда следует, что переменные Y и X являются некоррелированными, если

E{YX} = cov{Y,X} = 0.

Если переменная Y (при EY = 0) является условно независимой в среднем от переменной X, то это означает, что

E{YX} E{Y} = 0.

Это условие более строгое, чем нулевая корреляция, поскольку = 0 предполагает, что E{Yg(X)} = 0 для любой функции д. Если переменные Y и X независимы, то снова это условие более строгое, и оно означает, что

E{9l{Y)g2{X)} = E{9l(Y)}E{g2(X)}

для произвольных функций ji и йЛегко проверить, что это условие предполагает условную независимость в среднем и нулевую корреляцию. Отметим, что E'jFlX} = 0 необязательно означает, что E{XY} = 0.

В.6. Нормальное распределение

В эконометрике нормальное распределение играет центральную роль. Функция плотности для нормального распределения со средним jjl и дисперсией сг2 имеет вид

U ^ 1 { 1 (у x/W i 2 а2

Этот факт обычно обозначается как Y ~ Л/"(/і, сг2). Легко проверить, что нормальное распределение является симметрическим. Стандартное нормальное распределение получается, если і — 0 и сг = 1. Отметим, что стандартизированная переменная (F — /і)/сг распределена, как Л/*(0,1), если Y ~ Л/*(/х, сг2). Плотность стандартного нормального распределения, как правило, обозначаемая 0, имеет вид

ф{у) = vfeexpHy2

Полезное свойство нормального распределения состоит в том, что линейная функция от нормальной переменной является также нормальной. Таким образом, если Y ~ Л/*(/х, сг2) тогда

aY + b ~ Я(ац + 6, а2 а2).

Кумулятивная функция плотности нормального распределения выражается в виде

(у-(л)/(т

р{у<у} = р[Ц»<^] = ф(^)= J т*.

— оо

где Ф обозначает кумулятивную функцию плотности стандартного нормального распределения. Отметим, что Ф(у) = 1 — Ф(—у) из-за симметрии.

Симметрия также подразумевает, что третий центральный момент нормального распределения равен нулю. Можно показать, что четвертый центральный момент нормального распределения имеет вид

E{(Y-rf} = 3*

Отметим, что это подразумевает это Е{У4} = 4<т4.Как правило, эти свойства третьего и четвертого центральных моментов используются в тестах проверки нормальности распределения.

Если вектор (У, ХУ имеет двумерное нормальное распределение с вектором средних р = (цу, рхУ и ковариационной матрицей

Е = ( Gl ау*

СГух (УІ )

обозначаемое, как (У, X)' ~ Л/*(/х, S), то функция совместной плотности распределения имеет вид

f(y,x) = f(yx)f(x),

где как условная плотность переменной Y при условии заданной переменной X, так и маргинальная плотность X являются нормальными. Условная функция плотности задается как

,[2^7 12 ег у Ух

= г — ехр <j ^

ух

где — условное математическое ожидание переменной Y для данного X, имеет вид

*ух ГУ ' 2 ах

і ®УХ ( Vyx = Ну + —(Х-Нх),

}ух

а avx ~~ условная дисперсия переменной Y для данного X,

2

2 2 2/1 2

<7у|* = ~ ~Z2 = ауУ1 ~ Pyxh их

с Pyx j обозначающим коэффициент корреляции между переменными

и X. Эти результаты имеют некоторые важные следствия. Во-первых, если две (или больше) переменных имеют совместное нормальное распределение, то все маргинальные и условные распределения также нормальны. Во вторых, условное математическое ожидание одной переменной при заданном значении другой(их) переменной является линейной функцией (со свободным членом). В-третьих, если рух — 0, то из этого следует, что f(yx) = /(у), так что

f{yx) = f(y)f(x),

и переменные Y и X независимы. Таким образом, если переменные

и X имеют совместное нормальное распределение с нулевой корреляцией, тогда, они автоматически независимы. Вспомним, что в общем случае для независимости имеется более строгое требование, чем некоррелированность.

Другой важный результат состоит в том, что линейная функция от нормальных переменных является также нормальной, то есть, если (У, ХУ ~ Л/*(/х, Е), тогда

аУ + ЬХ ~ Я{aiiy + b/ix, a2 a2 + b2a2x + 2abayx).

Эти результаты можно обобщить на if-мерное нормальное распределение. Если if-мерный вектор имеет нормальное распределение с вектором средних /і и ковариационной матрицей Е, то есть

у ~ЛГ(а*,Е),

—*

то справедливо, что распределение І2У, где R — J х К матрица, является J-мерным нормальным распределением, заданным как*)

RY~Af(Rfr KER').

В моделях с ограниченными зависимыми переменными мы часто сталкиваемся с формами усечения. Если случайная переменная Y имеет плотность /(у), то распределение У, усеченное снизу в данной точке с (У > с), дают

f (

f{yY > с) = -, если у > с, и 0 в противном случае.

-Г {У > с}

Если У — стандартная нормальная переменная, усеченное распределение У > с имеет среднее значение

E{YY>c} = X1(c),

где

Ai(c) =

Ф(с)'

и дисперсию

>с} = 1-Лі(с)[А1(с)-с].

Если распределение усечено выше (У < с), то справедливо, что

Я{У|Г <с} = А2(с),

с

Л2(с) = w

Это утверждение справедливо при условии, что матрица преобразования (R) является матрицей полного ранга (примеч. научн. ред. перевода).

Если Y имеет нормальную плотность со средним ц и дисперсией сг2, то усеченное распределение Y > с имеет среднее значение

E{YY >с} = /і + аАі(с*) > //,

где с* = (с — /і)/<7, и, точно так же

£{Y|Y < с} /х + <тА2(с*) <

Когда вектор (У < X/ имеет двумерное нормальное распределение, как и выше, мы получаем, что

E{YX >с} = »у + ^{Е{ХХ > с} цх] =»у + ^А!(с*).

сх ax

Подробности можно найти в книге (Vaddala, 1983, Appendix).

В.7. Распределения, связанные

с нормальным распределением

Помимо нормального распределения важными являются несколько других распределений. Сначала, мы определим хи-квадрат распределение следующим образом. Если Yi,... , Yj — совокупность независимых стандартных нормальных переменных, то справедливо, что

имеет хи-квадрат распределение с J степенями свободы. Мы обозначим £ ~ Xj • Более обще, если Y,... , Y3— совокупность независимых нормальных переменных со средним i и дисперсией сг2, то тогда следует, что

имеет хи-квадрат распределение с J степенями свободы. Более обще, если Y = (Yi,... , Yj)f — вектор случайных переменных, который имеет совместное нормальное распределение с вектором средних i и (невырожденной) ковариационной матрицей Е, то из этого следует, что

Если £ имеет хи-квадрат распределение с J степенями свободы, то справедливо, что Е{£} = J и V{^} = 2J.

Теперь рассмотрим t-распределение (или распределение Стью-дента). Если X имеет стандартное нормальное распределение, X ~ Л/*(0,1), и £ ~ \%j, и если X и £ независимы, то отношение

_ X

имеет і-распределение с J степенями свободы. Как и стандартное нормальное распределение, і-распределение является симметрическим около нуля, но оно имеет более тяжелые хвосты, особенно для малых J. Если J стремится к бесконечности, то ^-распределение стремится к нормальному распределению.

Если £1 ~ Xj и £2 ~ Xj? и если £1 и £2 независимы, то отношение

f = &м

имеет распределение с «Л и J2 степенями свободы в числителе и знаменателе соответственно. Из этого легко следует, что обратное отношение

также имеет F-распределение, но с J2 и Ji степенями свободы соответственно. Таким образом, F-распределение является распределением отношения двух независимых хи-квадрат разделенных переменных, деленных на их соответствующие степени свободы. Если Ji = 1, то £1 — квадрат нормальной переменной, скажем, £1 = X2, и из этого следует, что

(2=(тш) =mr!~F]>Таким образом, F-распределение с одной степенью свободы числителя является просто квадратом і-распределения. Если J2 является большим, то распределение

хорошо аппроксимируется хи-квадрат распределением с J степенями свободы. Таким образом, для большого J2 знаменатель пренебрежимо мал.

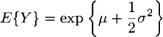
(сравните с неравенством Йенсена выше).

И, наконец, мы рассмотрим логарифмически нормальное распределение. Если log Y имеет нормальное распределение со средним jjl и дисперсией <т2, тогда Y > 0 имеет так называемое логарифмически нормальное распределение. Плотность логарифмически нормального распределения часто используется, чтобы описать распределение генеральной совокупности (трудового) дохода или распределения доходностей активов (см. Campbell, Lo, MacKinlay, 1997). Если E{ogY} = і, то справедливо, что