Глава 9 системы регрессионных уравнений
Глава 9 системы регрессионных уравнений
Задача 9.1
Рассмотрим следующую модель:
 | |||
 | |||
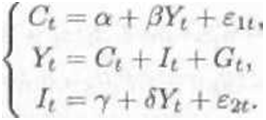Решение I
Введем обозначения:
 |
z, =
Тогда модель может быть записана в матричной форме:
Bzt + Twi = et,
где
1 О -0 В= 0 1 -8
-1 -1 1
Приведенная форма записывается в ваде:
-7 О
О О
-1
 | |||
 | |||
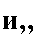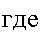в-1 =
1-0-6
1-6 0 0 5 1-0 S 1 1 1
П =
1-0-6
| Га — 6а 4/з7 | 0" | 4 | ||
| 7 — 0*у 4а<5 | 6 | — | ті | |
| а 47 | 1 | 4 | 4 |
*)
Ha шесть коэффициентов приведенной формы наложены два огранн-ения:
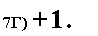7ГуТТС + 7Г, ,
7Гу= 7Г(-
(**)
Покажем, что по заданным коэффициентам приведенной формы (элементам матрицы П), удовлетворяющим ограничениям (**), можно единственным образом восстановить коэффициенты а, /3, 7 и б, т. е. уравнение (П -|Г — 0 всегда имеет единственное решение. В самом деле, из (*) получаем (если тгу ф 0):
8 =
7Г
1 < V 1 1
о 47 =
7Г
1 1
а{-6) + 10
7Г
Подставив 5 и /3 в последние два уравнения, получим систему относи-іьпо 7 и а:
7Г?.
Oc + J =
-і
а 1
7Г
1
V
7Г,
+ 7-f = —
7Гі
О
Подставляя у = —— а во второе уравнение, получаем:
7TV
о:
1
7Г!
7г;
7Ґ
7Г
о
y
1
— а
7Г
7Г
Отсюда
0(Ку Г») 7г£.) = 7Г£
44
или, в силу (**),
 |  | ||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
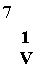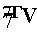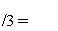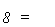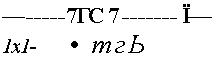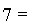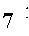Задача 9.2
ч
Рассмотрим проблему идентифицируемости каждого из уравнений в следу ющей модели:
Pt + РпЩ
+ 7nQ<
+ 7ізЛ-і
= Єн,
+ 732-Si + 7ззР/-і + 7:мМ'(-п = Єзь
где Pt, Wt, Nt индекс цен, зарплата, профсоюзный взнос соответствен!! (эндогенные переменные), a Qt И 5< — производительность труда и кол чество забастовок (экзогенные переменные). Как выглядят порядковое и ранговое условия, если известно, что:
а) 711 =0,
б) 021 = 722 = 0,
в) 7зз = 0?
Решение
При исследовании идентифицируемости уравнений в системе одновреме ных уравнений при наличии простейших ограничений (равенство нулю го или иного коэффициента) можно воспользоваться следующим практическим приемом, суть которого может быть продемонстрирована на данном примере.
В нашем случае мы имеем три эндогенные неременные — Pt, Wt, Nt, экзогенные — Qt, St и две легированные эндогенные — Pt-i, И V— і ПреД ставим исходную систему в виде следующей таблицы, в ячейках которо стоят коэффициенты при соответствующей переменной в соответствуют^ уравнении:
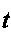
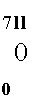е уравнение
е уравнение
е уравнение
Pt
1
021
0
Wt
012 1
032
Nt Q
0
023 1
St
0
722 732
Pt
7i3 0
733
i
Wt-0
724 734
Тогда выполнение порядкового условия эквивалентно тому, что в к дом уравнении число нулей не меньше числа уравнений минус 1 (|J IiaJ
случае — 2). Отсюда следует, что для каждого уравнения порядковое условие выполнено даже без дополнительных ограничений а), б), в). Проверка выполнения рангового условия для любого уравнения осуществляется так. Надо взять какой-либо нулевой коэффициент этого уравнения, выписать весь соответствующий столбец таблицы (исключая этот нулевой коэффициент), повторить эту операцию для всех нулевых коэффициентов уравнения и получить матрицу, число строк которой будет на единицу меньше числа уравнений, а число столбцов не меньше, чем число уравнений минус 1, в силу выполнения порядкового условия. Тогда выполнение рангового условия эквивалентно тому, что построенная матрица имеет полный ранг (т.е. число уравнений минус 1).
В пашем случае соответствующие матрицы таковы:
1-е уравнение —
2-е уравнение •
3-е уравнение
023 122 724
1 732 734
I
7И 713
711
О
0 7зз
1
021
Тогда получаем:
а) если 7i ] = 0, то первое уравнение идентифицируемо, а второе и третье
нет;
б) если 02} = 722 = 0, то первое и второе уравнения идентифицируемы,
^третье нет;
в) если 7зз = 0, то первое и третье уравнения идентифицируемы, а второе
нет.
•адача 9.3
7i2X2t = Єи
+ 723^3* = C2ti
733^31 = єз*Опишите процедуру оценивания каждого из уравнений следующей системы:
УП + 012У21 + 711
У21 + 721
032У21 + Узь + 731
>ешение
Как и в задаче 9.2, составим таблицу.
| У и | h'2t | . У3t | const | 3*2/ | Ш | |
| е уравнение | 1 | 0X2 | 0 | 7и 1 | 712 | 0 |
| еуравнение | 0 | 1 | 0 | 721 | 0 | 723 |
| е уравнение | 0 | 032 | 1 | 7зі | 0 | 7зз |
Применяя процедуру, описанную в задаче 9.2, получаем, что первое и і второе уравнения идентифицируемы, а третье нет, несмотря на то, что для каждого уравнения выполнены порядковые условия. Согласно двухшагово-му методу наименьших квадратов, для оценивания первого уравнения надо осуществить регрессию у2/ иаагге» x3t и константу, получить прогнозные значения у21, а затем провести регрессию ум на У2и 32t» и константу. Для оценивания второго уравнения достаточно провести регрессию У2і на х*м и константу.
Задача 9,4
Рассматривается следующая система уравнении:
Ун = 7ю * &12У2І + 0ЇЩІ + \%1Щ + 7i2^2t +
У2і = 720 + 02Уи + 721-Ти + gfti
Узг = 7зо + tklVtt + 032У21 + 7зі^и + 7зз^зі + £з*
Идентифицируемо ли каждое из уравнений системы? Что получится, если применить к первому уравнению двухшаговый метод наименьших квадратов?
Решение
Составим таблицу (ср. задача 9.2).
| Уи | У:и | const | Х2І | хзі | |||
| 1-е уравнение | -1 | 012 | 0X3 | 7ю | 7п | 712 | 0 |
| 2-е уравнение | 021 | -1 | 0 | 720 | 721 | 0 | 0 I |
| 3-е уравнение | 0zx | 032 | -1 | 7зо | 731 | 0 | 7зз |
Для первого и третьего уравнений не выполнены порядковые условия, следовательно, они не идентифицируемы. Для второго уравнения выполнено как порядковое, так и ранговое условие, поэтому оно идентифицируемо;
Применение к первому уравнению двухшагового метода наименьш квадратов приведет к системе с точной коллинеарностью.
Задача 9.5
Задана система одновременных уравнений (ї/і, уг, Уз — эндогенные переме ные).
Ун = 7ю + 02У2ь +7пяи +€Щ
У2І f 720 + 023УЗІ + l2X -Ь 723^3* + £2£>
Узг = 0зУи + 032У21 + 731 хп + 732^2/ + 7зз#з* + ЄЩ
а) Для каждого из трех уравнений определите, выполняются ли порядкои ранговые идентифицируемости. • ■ ^^^^^Г^Е
б) Повторите п. а) при дополнительном оі раннчении: 73»=,»^^^^ш
в) Пов'л>рите п.а) ним доиолиителыи>м <►граничении: 732^Вн^^^^^^Ы
г) Повторите п. а) при дополнительном ограничении: 732 = 7зз
Решение
Составим таблицу (ср. задача 9.2).
| У и | У21 | Узі | const | X2t | *3t | ||
| 1-е уравнение | -1 | Р2 | 0 | 7io | 7П | 0 | 0 |
| 2-е уравнение | 0 | -1 | #23 | 720 | 721 | 0 | 723 |
| 3-е уравнение | Ді2 | -1 | 0 | 7зі | 732 | 733 |
а) Как видим, для первого и второго уравнений порядковые условия выполняются (число нулей в строке не меньше 2). Для третьего уравнения порядковое (а значит, и ранговое) условие не выполняется.
Матрицы для проверки рангового условия доя первого и второго уравнений следующие:
1-е уравнение —
2-е уравнение —
'023 -1
-1
0 723
732 7зз
0
7зз
Ранговые условия выполняются для обоих уравнений, следовательно, первое и второе уравнения идентифицируемы.
б) Если положить 7з2 — 0, то порядковые условия для первого и второго уравнений не изменятся, а для третьего уравнения порядковое условие становится выполненным.
Ранговое условие для первого уравнения выполняется, для второго и третьего нет. Следовательно, только первое уравнение идентифицируемо.
Если положить 7з2 = 1, то для проверки ранговых условий в нервом и втором уравнениях достаточно подставить 732 = 1 в матрицы из п. а). Ранговые условия выполняются, значит, первое и второе уравнения идентифицируемы.
Чтобы проверить идентифицируемость третьего уравнения, сделаем замену переменной: положим 234 = уы X2t Тогда таблица примет вид:
3-е уравнение —
7ш 0
720 023
Ее ранг равен 2, следовательно, третье уравнение идентифицируемо.
г) Если положить 7з2 = 7зз» то аналогично п. в) подставим это условие в матрицы из п. а) и убедимся, что первое и второе уравнения остались идентифицируемыми.
Чтобы проверить идентифицируемость третьего уравнения, сделаем замену переменной: положим Z2t ~ хм + ХЦ. Тогда таблица примет вид:
3-е уравиепие —
710 О
720 723
Ее рані' равен 2, следовательно, третье уравнение идентифицируемо.
Задача 9.6
Рассматривается модель, состоящая из двух внешне не связанных уравнений (SUR):
Vti =0i -Fen, J
Уі2 =02Xt+St2
По 50 наблюдениям (по каждому уравнению) получены следующие рез,У-^ таты: £хь = 100, £х2 = 600, £зд(1 = 60, Щхгуь2 = 50, £>і = l°{h £У« = 500, gj/tif 2 = 150, Х>2 = 50, £у?3 = 90.
а) Напишите формулу для GLS-оценки параметров 0, 02б) Найдите OLS-оценку этих параметров.
в) Найдите SUR (FGLS)-oueHKy этих параметров и оцените матрицы ковариаций этих оценок. ■ ^^^^^^4ш.
Решение m# ^^Ci
а) Обозначим ковариационную матрицу вектора [є\, £(.2]' через
Oil °2
Модель SUR, следуя обозначениям из разд. 9.1, можно записать в виде
С у = Х/3 + е,
Их
02
Ух
У2
где
. х =
. є =
, 0 =
У
~Х, О
О Х2
Є2
Опенка ^Зсьб равна:
ДоЬЗ^ХЧГ'ХГ'ХЇГ^.
Матрица О-1 равна:
і
(J22 —С 12
0[СГ22 ~ Щп ~°*Г2 17п
ГГ1 = 5Г1 ®/„ =
.2
Матрица X'fi 'X равна:
X'ft 'X
]
(7\022 &12
(Т22« — 012 Е а'<
~0Ї2І>1 0*22 ЕЛ'?
Вектор Х'П'""у равен:
'о 1.
Х'П 'у =
^11^22 ?|2
022 Е ум *ria£V«3
-012 Е .ї-Ч.у/1 + Oil 52 **Уй
Матрица (Х'П 'X)"1 равна:
'r»-l 011022 ~ 012 ГЛі Е^? 0*12 £)Ж
Oil 0*22™ Ел;? (Е-^
012
Оценка ySc:ls равна:
і
о №l СГ22 E A E уп O-l 10-12 E -Г? E ?/i2
Ші^22п£а| щ (E-Tt)
0?2 Е xt X] $t»M + о-! іffi2 E x< E ЭД12)»
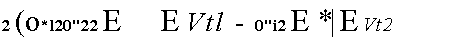І2 =
0ц 022'>Е-т? °и (Ext) 0-120*22" E xtVa +о-ца22пЕ^гг/і2)-
б) МНК-оценки параметров 0 и 02 получаются оцениванием двух уравнений отдельно. Поэтому
п*-*50 3' 02 5>Г " 600 -°-0833' JV/
в) Сначала оценим параметры матрицы Е и оценим ковариационную матрицу оценки 3ols-
т
71
/1
Еї/м (ЕЫ:
7v
500 _ 1502 _ 50 502" ~ '
<?22
= 0.917.
1^2 1Г / ЕХ'У'2 V Ез 50 (50)2
50 50 • 000
п Е а'?
=
Е
ті
IV
= ЛулУг2 Еш Ei/t2 _ Е^Уи Т,хіУг2 ^ Еуп Е-^У'зЕ^
п2ї>?
50
502
50 • ООО
170 150-50 200-50 150-50-100
502•600
= 0.567.
Ковариационная матрица оценки /?ous равна:
-і
I о о 1
1 п 0 0 1
"Е1? L ?іа °22п
= 0.02,
1J
і • 600
50 • 600 0.917-50
50 • 600 0.567 • 100
50 • 600
Подставим в эту формулу оценки с?,-, и получим:
= 0.00153,
V( А) =
0.00189.
v(A) =
C^(A,A) =
Подставив оценки дц в формулу для оценки /3gls> получим значения
0ЦЄИОК &FGLS- I p'^^j^ I
Л, 2.549, 02 0.135. Ш Ж Ковариационная матрица оценки /3GLS равна
, v(pGUi) = (xn-1x)
Подставив оценки 9\% в формулу для получаем:
У{0) = 0.0147, V(/?2) = 0.00112, Co^(0Xl02) = 0.00139.
Обсуждение Сборник задач к начальному курсу эконометрики
Комментарии, рецензии и отзывы