Раздел з проверка гипотез, выбор «наилучшей» модели и прогнозирование по оцененной модели тема 3.1 проверка статистических гипотез о значениях отдельных коэффициентов и общей линейной гипотезы

Раздел з проверка гипотез, выбор «наилучшей» модели и прогнозирование по оцененной модели тема 3.1 проверка статистических гипотез о значениях отдельных коэффициентов и общей линейной гипотезы

В примере 2.2.2 был построен 95\%-й доверительный интервал для параметра в2 в виде:

02 ~ W15)^2 <в2<в2 +/а975(15)54,

т.е.

-0.0075 < в2 < 0.2580.

Полученный результат следует интерпретировать следующим образом: при любом истинном значении параметра в2 вероятность накрытия этого значения построенным доверительным интервалом равна 0.95.

Рассмотрим значение в2 = 1, построенный интервал его не накрывает. Однако если в2 действительно равняется 1, то вероятность такого ненакрытия равна: 1 0.95 = 0.05. Таким образом, факт ненакрытия значения в2 1 построенным интервалом представляет (в случае, когда в2 = 1) осуществление довольно редкого события, имеющего малую вероятность 0.05. И это дает основания сомневаться в том, что в действительности в2 = 1.

То же самое относится и к любому другому фиксированному значению в2, не принадлежащему указанному 95\%-му доверительному интервалу: предположение о том, что в действительности в2 = в°2, представляется маловероятным.

Априорные предположения о значениях параметров модели называют в этом контексте статистическими гипотезами (statistical hypothesis). О базовой проверяемой гипотезе говорят как об исходной — нулевой (null), ее обозначают Н0. Таким образом в последнем случае имеем дело с гипотезой

Н0: в2

■ el

В соответствии со сказанным выше такую гипотезу естественно отвергать (отклонять), если значение в не принадлежит 95\%-му доверительному интервалу для #2, т.е. интервалу [-0.0075, 0.2580].

Вспомнив, как этот интервал строился, заметим, что в не принадлежит этому интервалу тогда и только тогда, когда

0 2 ~~ @2

> ^0.975 (1^)»

т.е. когда наблюдаемое значение отношения

0~> — $?

«слишком велико» по

абсолютной величине. Последнее означает «слишком большое» отклонение оценки в2 от гипотетического значения в параметра в2 по сравнению

с оценкой sq2 значения ^D(d2) — корня из дисперсии оценки этого параметра. Итак, будем отвергать гипотезу Н0 : в2 = в, если выполнено неравенство

$2 ~~ 6 2

0.975

(15).

(3.1)

02

Однако это неравенство может выполняться и тогда, когда гипотеза Я0 верна, т.е. когда в2 = в°2. Вероятность такого события равна: 1 0.95 = 0.05. Следовательно, если в действительности в2 = в2, но неравенство (3.1) выполняется, то в соответствии с принятым соглашением отвергаем гипотезу Я0 и совершаем при этом ошибку 1-го рода (error of the first kind). Вероятность ошибки 1-го рода равна здесь 0.05, т.е. такая ошибка происходит в среднем в 5 случаях из 100.

Если бы мы выбрали произвольный доверительный уровень 1 а, то отвергали бы гипотезу Я0 : в2 = в при выполнении неравенства

0 2 ~ в

>>,_Л15),

о2

и ошибка 1-го рода допускалась в среднем в 100а случаев из 100. Точнее, вероятность ошибки 1-го рода была бы равна а:

Р{#0 отвергается | Я0 верна} = а.

Правило решения вопроса об отклонении или неотклонении статистической гипотезы Я0 называется статистическим критерием проверки гипотезы (statistical test of hypothesis) Я0, а выбранное при формулировании этого правила значение а называется уровнем значимости критерия (significance level).

В практических исследованиях по умолчанию обычно используют уровень значимости а = 0.05, хотя иногда используют и другие уровни значимости (например, а = 0.01 или а = 0.10). Выбор большего или меньшего значения а определяется степенью значимости для исследователя исходной гипотезы Я0. Скажем, выбор между а = 0.05 и а = 0.01 в пользу а = 0.01 означает, что исследователь заранее настроен в пользу гипотезы Я0, и ему требуются очень весомые аргументы против этой гипотезы, чтобы отказаться от нее. Выбор же в пользу уровня значимости а = 0.05 означает, что исследователь не столь сильно отстаивает гипотезу Я0 и готов отказаться от нее и при менее убедительной аргументации против этой гипотезы.

Заметим только: если в рассматриваемой ситуации выбираем меньшее значение а и тем самым уменьшаем вероятность ошибки 1-го рода, то уменьшаем также и вероятность отвергнуть гипотезу Н0 : в2 = в2, когда в действительности в2 = в * в. Последнюю вероятность называют мощностью (power) рассматриваемого критерия при альтернативе в2 = в.

В реальных ситуациях статистические критерии часто имеют довольно низкую мощность, так что рассматриваемая нулевая гипотеза отвергается соответствующим критерием довольно редко и в случаях, когда она неверна. Поэтому если некоторая гипотеза Я0 оказалась не отвергнутой статистическим критерием, правильнее говорить именно о неотвержении этой гипотезы, а не о ее принятии.

Всякий статистический критерий основывается на использовании той или иной статистики (статистики критерия, тестовой статистики — test statistics), т.е. случайной величины, значения которой могут быть вычислены (по крайней мере, теоретически) на основе имеющихся статистических данных и распределение которой известно (хотя бы приближенно).

В нашем примере критерий для проверки гипотезы Я0 : в2 = в основывался на использовании /-статистики (t statistic)

02 — в2

значение которой можно вычислить по данным наблюдений, поскольку в —

заданное число, а в2 и s$2 вычисляются по данным наблюдений. Критерии,

основанные на использовании /-статистик, называют /-критериями (t tests).

Каждому статистическому критерию соответствует критическое множество (critical region) R значений статистики критерия, при которых гипотеза Я0 отвергается в соответствии с принятым правилом. В нашем примере таковым является множество значений указанной /-статистики, превышающих по абсолютной величине значение / „(15).

1 2

Итак, статистический критерий определяется заданием:

а) статистической гипотезы Я0;

б) уровня значимости а;

в) статистики критерия;

г) критического множества R.

Можно подумать, что пункты б) и г) дублируют друг друга, поскольку в нашем примере критическое множество R однозначно определяется по заданному уровню значимости а. Однако одному и тому же уровню значимости можно сопоставлять различные критические множества, что дает возможность выбирать множество R наиболее рациональным образом — в зависимости от выбора гипотезы Н0 (выбор наиболее мощного критерия).

В компьютерных пакетах программ статистического анализа данных первоочередное внимание уделяется проверке гипотезы

Я0: д. = 0

в рамках нормальной линейной модели множественной регрессии

Уі=0Хп+... + 0рхір+єі9 i = l л,

с et ~ i.i.d. N(0, а2). Эта гипотеза соответствует предположению исследователя о том, что j-я объясняющая переменная не имеет существенного значения с точки зрения объяснения изменчивости значений объясняемой переменной у, так что она может быть исключена из модели. Для соответствующего критерия:

а) Я0: 9 = 0;

б) уровень значимости а по умолчанию обычно выбирается равным 0.05;

в) статистика критерия имеет вид:

если гипотеза Я0 : ^ = 0 верна, то эта статистика имеет ^-распределение Стьюдента с(п-р) степенями свободы:

-J—Kn-p);

\%

в связи с чем ее обычно называют /-статистикой (t statistic) или /-отношением (t ratio);

в1

г) критическое множество имеет вид:

>К_М~р)-

При этом в распечатках результатов регрессионного анализа (т.е. статистического анализа модели линейной регрессии) сообщаются:

значение оценки #у параметра Oj в графе «Коэффициенты» (Coefficients)',

значение знаменателя /-статистики в графе «Стандартная ошибка» (Std. Error);

значение отношения —— в графе «/-статистика» (t statistic).

Сообщается также Р-значение (P-value), т.е. вероятность того, что случайная величина, имеющая распределение Стьюдента с (п р) степенями свободы, примет значение, не меньшее по абсолютной величине, чем наблю-

денное значение

0,

, — в графе «Р-значение» (P-value или Probability).

В отношении полученного Р-значения возможны следующие варианты. 1. Если Р-значение меньше выбранного уровня значимости а, это равно-сильно тому, что значение /-статистики попало в область отвержеsa

ния гипотезы Н0 : 0j = О, т.е. Я0 отвергается.

в,

> t а (п р). В этом случае гипотеза

1-2

не попало в область от2. Если Р-значение больше выбранного уровня значимости а, это равно-сильно тому, что значение /-статистики

вержения гипотезы Н0 : в}О, т.е. потеза Н0 не отвергается.

в.

< t а (п р). В этом случае ги1-2

3. Если (в пределах округления) Р-значение равно выбранному уровню значимости а, то в отношении гипотезы Я0 : в}0 можно принять любое из двух возможных решений.

В случае, когда гипотеза Я0 : Oj, = 0 отвергается (вариант 1), говорят, что

оценка 6j параметра ^ статистически значима или статистически значимо отличается от нуля (statistically significant estimate). Это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели существенно для объяснения наблюдаемой изменчивости объясняемой переменной.

Напротив, если гипотеза Я0 : ^ = 0 не отвергается (вариант 2), говорят,

что оценка 0. параметра в} статистически незначима или статистически незначимо отличается от нуля (statistically non-significant estimate). В этом случае в рамках используемого статистического критерия мы не получаем убедительных аргументов против предположения о том, что dj = 0. Это соответствует признанию того, что наличие j-й объясняющей переменной в правой части модели несущественно для объяснения наблюдаемой изменчивости объясняемой переменной, следовательно, можно обойтись и без включения этой переменной в модель регрессии.

В соответствии с вышесказанным гипотезу Я0 : ^ = 0 часто называют гипотезой значимости для коэффициента 0j (hypothesis of the statistical significance of the coefficient 0j9 hypothesis that the coefficient 0is equal to zero).

Впрочем, выводы о статистической значимости (или незначимости) оценок того или иного параметра модели зависят от выбранного уровня значимости а. Так, решение в пользу статистической значимости оценки может измениться на противоположное при уменьшении а9 а решение в пользу статистической незначимости оценки может измениться на противоположное при увеличении а. Заметим только: выбор уровня значимости следует производить до обращения к самим статистическим данным, используя соображения, высказанные выше.

ПРИМЕР 3.1.1

В рассмотренном выше примере с уровнями безработицы в США имеем в распечатке R2 = 0.212375 и таблицу, полученную на основе протокола применения метода наименьших квадратов в пакете Econometric Views (табл. 3.1).

В самом протоколе оценивания в пакете Econometric Views результаты оценивания оформляются в следующем виде (табл. 3.2).

Соответственно при выборе уровня значимости а = 0.05 оценка коэффициента при переменной ZVET признается статистически незначимой (Р-значе-ние больше уровня значимости). Однако если выбрать а = 0.10, то Р-значение меньше уровня значимости, и ту же оценку коэффициента при переменной ZVET придется признать статистически значимой. ■

ПРИМЕР 3.1.2

При исследовании зависимости спроса на куриные яйца от цены (данные в табл. 1.7) получаем R2 = 0.513548 и табл. 3.3.

Здесь оценка коэффициента при объясняющей переменной CENA статистически значима даже при выборе а = 0.01, так что цена признается существенной объясняющей переменной. ■

ПРИМЕР 3.1.3

При регрессионном анализе потребления свинины на душу населения США в зависимости от оптовых цен на свинину (данные в табл. 1.8) получаем R2 0.054483 и табл. 3.4.

В этом примере оценка коэффициента при переменной CENA оказывается статистически незначимой при любом разумном выборе уровня значимости а(а = 0.01, а = 0.05, а=0.10).И

у/ Замечание 3.1.1. Ранее отмечалась возможность ложной линейной связи между двумя переменными и соответственно возможность ложного использования одной из переменных в качестве объясняющей для описания изменчивости другой переменной. Проиллюстрируем такую ситуацию на основе рассмотренных методов регрессионного анализа.

ПРИМЕР 3.1.4

В числе прочих подобных примеров мы получили модель линейной связи между мировым рекордом по прыжкам в высоту с шестом среди мужчин (Я, см) и суммарным производством электроэнергии в США (Е, млрд кВтч). Было указано на высокое значение коэффициента детерминации для этой модели: R2 = 0.900. Теперь можно привести результаты регрессионного анализа (табл. 3.5).

Формально переменная Я признается существенной для объяснения изменчивости переменной Е, так что здесь сталкиваемся с ложной (паразитной) регрессией переменной Е на переменную Я, обусловленной наличием выраженного (линейного) тренда обеих переменных во времени. ■

ПРИМЕР 3.1.5

Исходя из примера 2.2.3, обратимся снова к дефлированным (к 1972 г.) данным о совокупном располагаемом доходе (DPI) и совокупных расходах на потребление (CONS) в США за период с 1970 по 1979 г. Результаты регрессионного анализа приведены в табл. 3.6.

Как и было указано при рассмотрении примера 2.2.3, гипотеза о том, что постоянная составляющая в модели наблюдений равна нулю, отвергается на 5\%-м уровне значимости.■

Проверка значимости параметров линейной регрессии и уточнение спецификации модели с использованием F-критериев

В табл. 3.7 приведены ежегодные данные о следующих показателях экономики Франции за период с 1949 по 1960 г. (млрд франков, в ценах 1959 г.):

Y — объем импорта товаров и услуг во Францию;

Х2 — валовой национальный продукт;

Х3 — совокупное потребление домашних хозяйств.

Выберем модель наблюдений в виде:

У і = 0хп + Огхп + <V/3 + / = 1,..12,

где Xjj — значение показателя Xj в z-м наблюдении (/-му наблюдению соответствует (1948 + /)-й год, хп = 1 (значения «переменной»^, тождественно равной 1).

Предположим, что єи \% ~ i.i.d. N(0, а2) и значение а2 нам неизвестно.

При регрессионном анализе получим R2 = 0.9560 и результаты, приведенные в табл. 3.8.

Обратим внимание на выделенные жирным шрифтом Р-значения. В соответствии с ними проверка каждой отдельной гипотезы Н0 : в2 = 0, Н0 : въ 0 (даже при уровне значимости 0.10) приводит к решению о ее неотклонении. Соответственно при реализации каждой из этих двух процедур проверки

оценка соответствующего параметра (в2 или 93) признается статистически незначимой. И это выглядит противоречащим весьма высокому значению коэффициента детерминации.

В связи с этим возникает необходимость построения статистической процедуры для проверки совместной гипотезы

#0 : в2 = въ 0,

конкретизирующей значения не одного, а сразу двух коэффициентов.

Эта задача вкладывается в общую задачу проверки линейных гипотез (linear hypotheses) в нормальной линейной модели

М:# = ^хп+... + 0р i = l,..., л, п>р9

sX9...9s„~U.d.N(09 сг2), с целью уточнения спецификации модели. Линейные гипотезы имеют вид:

апвх+... + аХрвр=сх

aqX9x+... + aqp0p=cq9 где akj иск(к= 1,q9 j = 1, ...9р) — заданные числа.

Предполагается, что линейные комбинации в левых частях не дублируют друг друга, точнее, векторы (аП9 аХр)Т9 (aql9 aqp)T линейно независимы. В этом случае говорят, что имеется q линейных ограничений (linear restrictions) на коэффициенты вХ9вр (на вектор в-(вХ9вр)т).

В матричной форме такая линейная гипотеза принимает вид:

где А

#о :А9=с9

матрица размера (q х р), имеющая полный строковый ранг, гапкЛ = q9

4р

А =

, с =

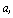яру

Если в — оценка наименьших квадратов вектора конечно, вряд ли стоит ожидать, что если гипотеза Я0 : Авс верна, то будет выполнено и соотношение Ав = с. Однако можно ожидать, что при этом разность Ав с не будет слишком сильно отклоняться от нулевого вектора, так что «слишком большие» отклонения А в с от нуля могут указывать на невыполнение гипотезы Н0 Авс. Для формализации этой идеи заметим: поскольку случайный

вектор в имеет р-мерное нормальное распределение Np(e, сг2(ХТХ)~х случайный вектор Ав с, получаемый из него линейным преобразованием и сдвигом, также имеет нормальное распределение, а поскольку rank^ = q, это будет ^-мерное нормальное распределение. Найдем математическое ожидание и ковариационную матрицу вектора А в с:

Е(Ав-с) = АЕ(в)-с = Ав-с,

Соу(Ав-с) = Соу(Ав) = ACov0)AT = а2 А(ХТ X)~l Ат.

Если гипотеза Н0 :Ав=с верна, то Е(А в с) = 0, так что

A0-c~Nq{p, <j2A(XTX)~l Ат).

Обозначим для краткости V = А(ХТХ)~1АТ. Поскольку a2V — ковариационная матрица ^-мерного нормального распределения, матрица V симметрична и положительно определена. Поскольку матрица V симметрична и положительно определена, такой же будет и обратная к ней матрица V~ Но тогда существует такая невырожденная (п х и)-матрица Р9 что Vх = РТР. Используя матрицу Р, преобразуем вектор А в с к вектору

(Ав-с)* =Р(Ав-с).

При этом Е(А в с)* = 0 и ковариационная матрица вектора (А в с)*

Cov((A в-сУ) = Cov(P(A в-с)) = Р Cov(A в-с)Рт= a2PVPT.

Но V= (V~Y = (РТРУтак что

Cov((A в-с)*) = а2Р(РтРу1 Рт = ст2РР-{ (Рт )-1 Рт = a2Iq,

(Ae-cY~Nq(09<r2Iq).

Таким образом, компоненты вектора (А в с)* являются независимыми, одинаково распределенными случайными величинами, имеющими нулевое математическое ожидание и дисперсию <т2. Но тогда сумма квадратов этих компонент, предварительно разделенных на <т, есть сумма квадратов q независимых нормальных величин, имеющих стандартное нормальное распределение. А такая сумма по определению имеет распределение хи-квадрат с q степенями свободы. Остается заметить, что указанная сумма квадратов

нормированных на а компонент вектора (А 9 с)* равна

а'2(А в с)*|2 = <т~2р(А в с) |2 = а~2 [р(А 9-с)]Т [р(А в-с)}=

= а'2(Авс)т ртр(А 9-с) = а~2(А9cf V~l (А9-с) = = а'2 (А9с)т (а{ХтХ)~х Ат)а9-с).

Следовательно,

(А9-с)т (а(ХгХУ1 АтУ(А9-с)

■Г (?)•

С

При «слишком больших» отклонениях (А в с) от нуля получаются и «слишком большие» (положительные) значения последнего отношения. Таким образом, гипотезу Н0 : Ав= с естественно отклонять, если значения

этого отношения превышают квантиль Х-а(я) распределения хч)^ гДе а — выбранный уровень значимости статистического критерия.

Проблема, однако, в том, что значение дисперсии <т2 неизвестно исследователю. Преодолевается это затруднение аналогично тому, как это было сделано для получения f-статистики: неизвестное значение а2 заменяется его несмещенной оценкой S2.

Рассмотрим следующую статистику (F-отношение — F ratio, или F-ста-тистика — F statistics):

F_(A3-c)T {а(ХтХУ1 АтУ(Авc)/q S2

Представим ее в виде:

р _ а~2(АО-с)т(а(ХтХ)~1 Ат)Ав-c)/q a-2RSS/(n-p)

Если гипотеза Н0 : Ав-с верна, то в числителе этой дроби стоит деленная на q случайная величина, имеющая распределение Z2(<l)> а в знаменателе — деленная на (п р) случайная величина, имеющая распределение хп ~ Р)-Можно доказать, что эти две случайные величины независимы (подробнее см. (Магнус, Катышев, Пересецкий, 2005)). Но тогда по определению последнее отношение имеет F-распределение Фишера с q и (п р) степенями свободы:

F~F(q, п-р).

На этой основе строится F-критерий (F test) для проверки гипотезы Я0 : Ав = с в нормальной линейной модели с выполненными стандартными предположениями:

• при заданном уровне значимости а гипотеза Я0 : Авс отвергается, если наблюдаемое значение статистики F превышает критическое значение, равное FKp=F{_ a(q, п -р), т.е. если F>FX_ a(q, п -р).

С указанной F-статистикой связана статистика Вальда (Waldstatistic)

s

на основании которой строится критерий Вальда (Wald test) для проверки гипотезы Я0 : Ав-с. При этом используется тот факт, что при п -> оо случайная величина S2 сходится по вероятности к а2. Из этого факта и известной из курса теории вероятностей теоремы Слуцкого вытекает, что W имеет то же предельное распределение, что и отношение

(Авс)Т (а(ХтХ)~1 Ат У (А в-с)

а2

которое, как было сказано выше, имеет распределение х\<1)При использовании критерия Вальда гипотеза Я0 : Ав1 = с отвергается,

если выполняется соотношение W > Zi-аія) • Поскольку критическое значение Х-а(я) рассчитывается по предельному при п -> оо (асимптотическому) распределению статистики W, использование его оправданно при больших значениях п. Соответственно о критерии Вальда говорят как об асимптотическом критерии (asymptotic test). В противовес этому F-критерий, рассмотренный выше, является «точным», неасимптотическим критерием (non-asymptotic test) — в том смысле, что распределение F-статистики при любом конечном количестве наблюдений п > р имеет при сделанных предположениях F-pac-пределение F(q, п р), соответствующее этому количеству наблюдений.

Таким образом, если выполнена гипотеза Я0 : Ав= с (с q линейными ограничениями), то статистика

Г^(Ав-с)т(А(ХтХГ1АтУ(Аё-с)/д S2

имеет распределение F{q, п р), а значит, с вероятностью 1 а выполняется неравенство

F^Fx_a(q,n-p),

т.е.

(Ав-с)т(а(ХтХУ{ AT)A9-c)<qS2Fx_a(q, п-р).

Следовательно, если верна гипотеза

Я0:^=^°,...,^=^, т.е. Н0:6> = 6>

так что q = р и А = 1р (единичная матрица), то тогда с вероятностью 1 а выполняется соотношение

ф-в,)ТХТхф-в,) < pS2Fx_a(p,n-p),

определяющее 100(1 а)\%-й доверительный эллипсоид для в0 (имеющий уровень доверия /= 1 а).

При р = 2 получаем доверительный эллипс для коэффициентов модели.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Что такое статистический критерий? Опишите его структуру.

Как формулируется гипотеза значимости для отдельного коэффициента линейной эконометрической модели? Каким образом проверяется эта гипотеза?

Что такое статистически значимая (статистически незначимая) оценка коэффициента линейной эконометрической модели?

Как зависят выводы о статистической значимости (о статистической незначимости) оценок коэффициентов от выбора уровня значимости статистического критерия? Чем руководствуется исследователь при выборе уровня значимости статистического критерия?

Какой из двух уровней значимости — а = 0.10 или а = 0.01 — является более высоким? Как влияет выбор между уровнями значимости а = 0.10 и а = 0.01 на мощность статистического критерия?

Опишите использование /-критерия для проверки гипотезы о значении отдельного коэффициента линейной эконометрической модели.

Какие основные результаты линейного регрессионного анализа приводятся в протоколах оценивания?

Что такое Р-значение? Какие выводы делаются на основе этого значения при проверке гипотезы значимости для отдельного коэффициента линейной эконометрической модели?

Означает ли статистическая значимость оценки коэффициента при объясняющей переменной в линейной эконометрической модели наличие причинной связи между объясняющей и объясняемой переменными?

Какая гипотеза относительно коэффициентов линейной эконометрической модели называется линейной? Как такая гипотеза представляется в матричной форме?

Как выглядит F-отношение (F-статистика) для проверки линейной гипотезы относительно коэффициентов линейной эконометрической модели? Какое вероятностное распределение имеет это отношение в случае, когда проверяемая линейная гипотеза верна и выполнены стандартные предположения о модели?

Как выглядит статистика Вальда для проверки линейной гипотезы относительно коэффициентов линейной эконометрической модели? Чем она отличается от соответствующей F-статистики? Почему ее применение оправданно только при большом количестве наблюдений?

Как определяется доверительный эллипсоид (доверительный эллипс) для коэффициентов линейной модели?