Тема 7.2 подбор стационарной модели arma для ряда наблюдений

Тема 7.2 подбор стационарной модели arma для ряда наблюдений

Если предположить, что некоторый наблюдаемый временной ряд xl9 хп порождается моделью ARMA, то при этом возникает проблема подбора конкретной модели из этого класса. Решение этой проблемы предусматривает три этапа:

идентификация модели (identification stage);

оценивание модели (estimation stage);

диагностика модели (diagnostic checking stage).

На этапе идентификации производится выбор некоторой частной модели из всего класса ARMA, т.е. выбор значений р и q. Используемые при этом процедуры являются не вполне точными, что при последующем анализе может привести к выводу о непригодности идентифицированной модели и необходимости замены ее альтернативной моделью. На этом же этапе делаются предварительные грубые оценки коэффициентов аХ9 а2, ар9 bl9 bl9 bq идентифицированной модели.

На втором этапе производится уточнение оценок коэффициентов модели с использованием эффективных статистических методов. Для оцененных коэффициентов вычисляются приближенные стандартные ошибки, которые при дополнительных предположениях о распределениях случайных величин Х{9 Х29 ... дают возможность строить доверительные интервалы для этих коэффициентов и проверять гипотезы об их истинных значениях с целью уточнения спецификации модели.

На третьем этапе применяются различные диагностические процедуры проверки адекватности выбранной модели имеющимся данным. Неадекватности, обнаруженные в ходе такой проверки, могут указать на необходимую корректировку модели, после чего производится новый цикл подбора, и т.д. до тех пор, пока не будет получена удовлетворительная модель.

Разумеется, если уже имеется достаточно отработанная и разумно интерпретируемая модель эволюции того или иного показателя, можно обойтись и без этапа идентификации.

Если ряд порождается моделью ARMA(p, q)9 то в дальнейшем для краткости будем обозначать это как Xt ~ ARMA(p, q). Соответственно если ряд порождается моделью AR(p)9 то Xt ~ AR(/i), и если ряд порождается моделью MA(q)9 то Xt ~ МА(#).

Идентификация стационарной модели ARMA

Основной отправной точкой для идентификации стационарной модели ARMA является наличие различий в поведении автокорреляционных и частных автокорреляционных функций (ACF — autocorrelation function, PACF — partial autocorrelation function) рядов, соответствующих различным моделям ARMA.

О поведении автокорреляционных функций для различных моделей ARMA было сказано выше. Однако по поведению только автокорреляционной функции трудно идентифицировать даже порядок чистого (без МА составляющей) процесса авторегрессии. Решению этого вопроса помогает рассмотрение поведения частной автокорреляционной функции (PACF) стационарного процесса Хг Ее значение Ppart(k) на лаге к — частная автокорреляция {partial autocorrelation) — определяется как значение коэффициента корреляции между случайными величинами Хг и Xt+k9 очищенными от влияния промежуточных случайных величин Xt+ х,Xt+k_ х.

Это соответствует тому, что ppart(k) является коэффициентом при Xt_k в линейной комбинации случайных величин Xt_l9 Xt_k9 наилучшим образом приближающей случайную величину Хг Исходя из последнего, можно

показать (см., например, (Hamilton, 1994, р. 111)), что ppart(k) определяется как решение относительно ак системы первых к уравнений Юла — Уокера

p(s) = axp(s -1) + a2p(s 2) +... + akp(s -к), s = 1,2,... Д,

которую в этом случае удобнее записать в виде:

p(s )ах + p(s 2)а2 +... + p(s к)ак = p(s), s = 1,2,..., к,

подчеркивая, что неизвестными здесь являются al9 а2, ак9 а р( к), р(к 1) — известные коэффициенты. Исходя из этого и применяя правило Крамера решения системы к линейных уравнений с к неизвестными, находим, что вычисление PACF можно производить по формулам:

PPart(0) = h

l Ml)

МО M2)

/W(i) = /*i),

Р parti2) =

1 МО

Mi) і

р{2)-р\)

1-Р20) '

РраЛЗ) =

1	МО	МО
Ml)	1	Р(2)
Р(2)	МО	Р(3)
1	МО	Р(2)
МО	1	МО
Р(2)	МО	1

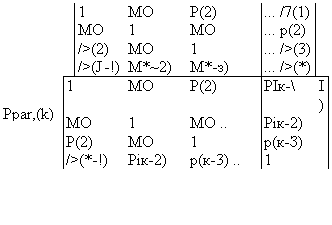Здесь определитель в числителе выражения для ppart(k) отличается от определителя в знаменателе этого выражения только заменой последнего столбца столбцом, состоящим из значений р(), р(2)9р{к).

Замечательным является тот факт, что если Xt — процесс типа AR(p), тогда

РраЛк) = ° ДДЯ Ь>р.

Это позволяет по графику PACF определять порядок процесса авторегрессии и отличать процесс авторегрессии от процессов скользящего среднего и ARMA(p, q) с q > 0.

Напомним, что зануление ACF после лага q соответствует процессу МА(#). Теперь же видно, что зануление PACF после лага р соответствует процессу AR(p). Поэтому идентификация этих моделей по ACF и PACF более определенна по сравнению с идентификацией моделей ARMA(p, q)cp*09q*0.

В то же время вместо неизвестных истинных последовательностей автокорреляций р(к) и частных автокорреляций ppart(k) приходится довольствоваться только их оценками — выборочной ACF (sample ACF — SACF), образованной выборочными автокорреляциями (sample autocorrelations)

1 Т~к

г(к) = ^±^-т = 4^, * = U.,r-i,

1 t = l

1 T

где jd-x = —^xt — оценка для ju = E(Xt); 1 T~k

y(k) = —— ju)(xt+k -fi)— оценка для y(k),

и выборочной PACF (sample PACF — SPACF), образованной выборочными частными автокорреляциями r^iK) (sample partial autocorrelations). Получить последние можно, заменив входящие в выражения для ppart(k) автокорреляции p(s) их оценками r(s). Однако проще поступить иначе. Исходя из того, что ppart(k) является коэффициентом при (Xt_k ju) в линейной комбинации случайных величин Xt_x -//, Xt_kju, наилучшим образом приближающей случайную величину Xt /л, можно просто методом наименьших квадратов оценить коэффициенты в модели

Xt = а + axXt_x + a2Xt_2 +... + akXt_k + ut

(в которой составляющая ut получается как разность

ut=Xt-(a + axXt_x + a2Xt_2 +... + akXt_k),

так что на нее не накладывается никаких предварительных ограничений). Полученная в результате оценка коэффициента ак и есть rpart(k).

Если у ARMA(p, q) процесса a(L)Xt = b(L)st все корни алгебраических уравнений a(L) = О и b(L) = О лежат за пределами единичного круга на комплексной плоскости, е19 єТ ~ i.i.d. и Е(є?) < оо, то указанные оценки /Ї, /(к), г(к) и rpart(k) являются состоятельными оценками для ju, у(к), р(к) и ppart(k) соответственно (см. (Hamilton, 1994, р. 199)). Но поскольку г(к) и rpart(k) всего лишь оценки для р(к) и ppart(k), то их наблюдаемые значения могут значительно отличаться от р(к) и ppart(k). В частности, если при некоторых к = кх ик = к2ъ модели, порождающей наблюдения, р(кх) = 0 и ppart(k2) = О, то, как правило, г(кх) * 0 и rpart(k2) Ф 0, что вносит дополнительную неопределенность в задачу идентификации. Более того, характер изменения теоретической автокорреляционной функции вовсе не обязательно будет воспроизводиться в ее выборочном аналоге — в выборочной автокорреляционной функции.

Тем не менее во многих случаях поведение теоретических ACF и PACF в какой-то мере отражается и на поведении их выборочных аналогов. Поэтому представление о поведении теоретических ACF и PACF может помочь в решении задачи идентификации соответствующих моделей в рамках общего класса моделей ARMA. Имея это в виду, сведем в табл. 7.3 свойства ACF и PACF для некоторых популярных моделей стационарных временных рядов.

Исходя из возможности идентификации моделей AR(p) и МА(#) по графикам функций г (к) и rpart(k) желательно иметь статистические критерии для

проверки гипотез о равенстве нулю тех или иных значений р(к) и ppart(k) на основе наблюдаемых значений г(к) и г^^к). Вопрос этот весьма сложный, ограничимся только двумя приближенными рецептами, которые предполагают гауссовостъ инноваций (т.е. что st — гауссовский белый шум).

lim E(r(k)) = p(k),

Г->оо

1. Если Xt — процесс типа МА(д), то и при больших Т

1 ( « ^

D(r(h))« + 2^р\]) 1 У=і

для k > q,

так что чем длиннее ряд наблюдений, тем надежнее выявляются нулевые значения р(к), k>q.

Более того, при больших Тик> q распределение случайной величины г(к) близко к нормальному. Отсюда вытекает, что естественный приближенный критерий проверки гипотезы #0 : «Xt — процесс типа МА(#)» состоит в том, чтобы отвергать эту гипотезу, если

для k>q.

Уровень значимости такого критерия приближенно равен 0.05.

В частности, если q = 0, то Xt ~ МА(0) — белый шум, и гипотеза Н0: «Xt — белый шум» отвергается указанным приближенным критерием при

2

к>0.

{k)\>-j=,

2. Если Xt — процесс типа AR(p), то при больших Тик>р распределение Графік) можно аппроксимировать нормальным распределением

rpart(k)*N(09T-l\% так что D(rpart(k)) « Г"1.

Следовательно, если гипотезу Я0 : Xt ~ AR(p) отвергать при

rpart(k)\>-lT> к> Р>

то получим критерий, уровень значимости которого приближенно равен 0.05.

С учетом двух указанных приближенных критериев в процедурах анализа временных рядов обычно предусмотрена распечатка графиков выборочных

2

ACF и PACF, на которые нанесены границы полосы ±-т=. В этих границах

с вероятностью, близкой к 0.95, должно заключаться при к > 0 значение г(к если Xt — белый шум, и при к > р значение rpart(k), если Xt ~ AR(p). Здесь следует сделать одно важное предупреждение: оба построенных критерия имеют уровень значимости, близкий к 0.05, только в том случае, когда гипотеза Н0 проверяется при некотором фиксированном к.

Что, однако, обычно происходит на практике? Рассмотрим это на примере смоделированного белого шума, график которого уже приводился ранее. Всего там было получено Т= 499 наблюдений хих29 х499. В табл. 7.4 приведены значения выборочных автокорреляционной и частной автокорреляционной функций для значений (лагов) к= 1, 2, 36.

2

В значениях ACF замечаем, что из полосы ±-7= = ±0.0895 выбивается

значение г(13) = 0.102. Означает ли это, что нужно отвергнуть гипотезу Я0: Xt — белый шум? В значениях PACF также обнаруживаем данные, выходящие за пределы этой полосы, что приводит к тому же вопросу.

Поскольку количество наблюдений у нас весьма велико (Т = 499), можно воспользоваться утверждением об асимптотической независимости rpart(k),

£=1,2,...

Пусть Вк — событие, состоящее в том, что rpart(k) выходит за пределы по-2

лосы ±-т=-. Вероятность этого события приближенно равна 0.05. Тогда веро-УІТ

ятность выхода за пределы полосы ровно двух (из 36) rpart(k к = 1,2, 36, приближенно равна:

р2 = С26 0.052(1 0.05)36"2 = ^1 0.052 • 0.9534,

и

Wi) = lg(630) + 21g(0.05) + 341g(0.95) = 0.560.

Отсюда находим: Р2 = 0.275, так что вероятность двух выходов из полосы графика выборочной PACF при рассмотрении 36 лагов вовсе не мала.

Что касается вероятности единственного выхода из полосы выборочной ACF, то здесь можно воспользоваться утверждением об асимптотической независимости г(к), к= 1,2, при условии, что Xt — белый шум (в случае МА(#) процесса с q > 1 это не так). При этом вероятность наличия единственного выхода выборочной ACF из все той же полосы приближенно равна:

Р2=С6 0.05(1-0.05)35,

так что lg(P,) = -0.780, откуда находим: рх = 0.166.

Рассмотренный пример показывает, что к интерпретации графиков выборочных ACF и PACF следует подходить достаточно осторожно1. Сюда же относится и то обстоятельство, что выражение, используемое при вычислении значений г(к) в пакете EViews, отличается от приведенного выше: в формуле для у (к) деление производится не на (Тк), а на Г. Последнее приводит к тому, что вычисляемая таким образом оценка для р(к) имеет смещение в направлении нуля.

В распечатках анализа временных рядов вместе с графиками выборочных ACF и PACF обычно указаны значения (7-статистики (Q-statistics), относящиеся к критерию для проверки гипотезы о том, что наблюдаемые данные являются реализацией процесса белого шума.

Существует несколько вариантов g-статистик. Одна из таких статистик — статистика Бокса — Пирса (Box-Pierce Q-statistic) была предложена Боксом и Пирсом в работе (Box, Pierce, 1970) и имеет вид:

м

Є = г£г2(*).

к =

Вспомним приведенные ранее результаты об асимптотической независимости г(1), г(2),г(М) в случае, когда Xt — белый шум, и отметим, что при

больших Т в этом случае г (к) «N(0,1), так что Tr2(k) « [N(0, I)]2 = J2(l) (заметим, что в этой ситуации не требуется гауссовость Xt — см. (Хеннан, 1974)). Отсюда вытекает, что при больших Г приближенно имеем

Против гипотезы Н0 говорят, скорее, большие значения этой статистики. Поэтому если выбрать уровень значимости равным 0.05, то естественно отвергать эту гипотезу при выполнении неравенства

Q>Z2o.9s(M),

где z$m9S(M) — квантиль уровня 0.95 распределения хи-квадрат с Мстепенями свободы.

В распечатках коррелограмм приводятся Р-значения (наблюдаемые уровни значимости) статистики Q для последовательных значений М1, 2,... При конкретном значении М гипотеза Н0 отвергается, когда соответствующее Р-значение меньше 0.05.

Впрочем, исследования показали, что статистика Бокса—Пирса плохо приближается распределением Х2(№) ПРИ умеренных значениях Г. Вместо нее

По этой причине в распечатках коррелограмм не будем давать графическое изображение границ полосы ± -j=r.

в таких случаях предпочтительнее использовать статистику Л юн га — Бокса

(Ljung-Box Q-statistic), предложенную в работе (Ljung, Box, 1979):

которая (при Т —>оо) также имеет асимптотическое распределение \%2(М), но ближе к этому распределению при умеренных значениях Г, чем статистика Бокса — Пирса. В пакете EViews значения статистики Л юнга—Бокса распечатываются вместе с приближенными Р-значениями, соответствующими распределениям z2(M) При практическом использовании g-статистик возникают определенные трудности. Посмотрим на таблицу Р-значений g-статистики Люнга — Бокса для рассмотренного выше примера с реализацией процесса белого шума (табл. 7.5).

Здесь Р-значения, соответствующие М14, 15, 17—22, меньше 0.05, так что формально при использовании статистики Люнга — Бокса с любым из этих значений М гипотеза Н0 : «Xt — белый шум» должна отвергаться. При остальных значениях М соответствующие Р-значения больше, чем 0.05, и гипотеза Н0 в этом случае не отвергается.

Какого-либо определенного рецепта, указывающего, как поступать в подобных ситуациях, на какое значение М следует ориентироваться, до сих пор не существует. Среди многочисленных исследований в этом направлении можно отметить работы (Kwan, 1996) и (Kwan, Sim, 1996).

Уже из рассмотренного примера ясно, что на этапе выбора подходящей модели среди множества ARMA моделей используемые процедуры являются не вполне точными и часто приводят к довольно неопределенным выводам. В результате этого этапа возможно оставление для дальнейшего исследования не одной, а нескольких потенциальных моделей. Более определенные выводы при выборе модели на первом этапе можно получить, применяя информационные критерии отбора моделей.

Использование информационных критериев. Если заранее ограничиться рассмотрением только AR моделей, т.е. полагать, что процесс Xt следует модели AR(k)

к

с неизвестным истинным порядком к, то для определения к в таких ситуациях долгое время использовался информационный критерий Акаике (Akaike information criterion —AIC) (см. Akaike, 1973). Согласно этому критерию среди альтернативных значений к выбирается такое, которое минимизирует величину

Ok

А1ОД = 1п<т,2+у,

где Т — количество наблюдений;

ак — оценка дисперсии инноваций st в AR модели £-го порядка1.

Для вычисления ак производится подбор модели к-то порядка с использованием уравнений Юла—Уокера

к

Ps=yEakjPs-j> У = 1

полученные оценки коэффициентов а0,у = 1, к, подставляются вместо akj в уравнение модели, /л заменяется на х, так что получаются оценки для et

к

it = (xt х) - akj (xt_j x),

7 = 1

после чего crk определяется как

1 т

Впоследствии было выяснено, что оценка Акаике несостоятельна и асимптотически переоценивает (завышает) истинное значение к0 с ненулевой вероятностью. В связи с этим были предложены состоятельные критерии, основанные на минимизации суммы

Приведенное выражение несколько отличается от предложенного в работе Акаике и используемого в пакете EViews. В нем опущено слагаемое, которое не зависит от порядка модели, а потому не влияет на результат выбора среди альтернативных значений к. Это замечание относится и к другим информационным критериям, рассмотренным ниже.

1п&\% + ксТ,

где ст = 0(Т~хпТ) (т.е. сг при Г -> оо имеет тот же порядок малости, что и ^^пГ).

Одним из таких критериев является часто используемый в настоящее время информационный критерий Шварца (Schwarz information criterion — SIC) (см. (Schwarz, 1978)):

SIC = ln<rj?+Jfc

In Г

Несколько позднее был предложен критерий Хеннана — Куинна (Нап-nan-Quinn information criterion — HQC) (см. (Hannan, Quinn, 1979)), в котором сТ = 2скТ~хЫпТ, о 1,

ттг. , л2 , 2с1п1пГ

UQ = lnak +k ,

обладающий более быстрой сходимостью к истинному значению к0 при Т оо. Однако при небольших значениях Т этот критерий недооценивает порядок авторегрессии.

ПРИМЕР 7.2.1

Рассмотрим модель процесса AR(2)

=1.2*M-0.36Jr,_2+£r Уравнение a(z) = 0 принимает в этом случае вид

l-1.2z + 0.36z2=0

и имеет двойной корень zx>2 = — >1, так что процесс, порождаемый такой

моделью, стационарен.

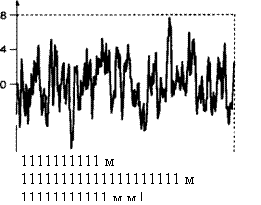Смоделированная реализация этого процесса для /= 1,2,..., 500 изображена на рис. 7.23.

х

Здесь из полосы ± —ч= = ±0.089 выходят только значения выборочной PACF, л/Т

соответствующие лагам к = 1, 2. В соответствии с приближенным критерием, указанным ранее, это приводит к неотвержению гипотезы Я0 : Xt ~ AR(2).

Для подтверждения этой гипотезы сравним значения информационных критериев Акаике и Шварца, получаемые при оценивании AR моделей 4-го, 3-го, 2-го и 1-го порядков, допускающих ненулевое математическое ожидание соответствующих AR процессов (табл. 7.6). Оба критерия выбирают модель AR(2).B

Если не будем ограничивать себя моделями AR и допустим, что модель, порождающая данные, имеет вид ARMA(p0, q0) (с неизвестнымир0,Яо)

a(L)Xt=b(L)et9

то для этого случая имеется несколько процедур оценивания пары (р0, q0 одну из которых сейчас рассмотрим (Kavalieris, 1991).

На первом шаге этой процедуры уже известными нам методами производится подбор модели авторегрессии AR(&):

к

Xt = YsakiXt-j+£t>

7 = 1

Построенная по этой реализации выборочная коррелограмма имеет следующий вид: вычисляются оценки коэффициентов а^9 7=1, к9 и на их основе получаются оценки инноваций

к

^k(0 = Xt-^lgXt-j'

7 = 1

Порядок к авторегрессионной модели на этом шаге должен быть достаточно высоким. Его можно выбрать путем сравнения значений критерия Акаике для оцененных моделей авторегрессии различных порядков. (Вспомним, что критерий Акаике склонен завышать порядок модели, а это в данном случае как раз и устраивает нас.)

На втором шаге берутся регрессии .Y, mXt_j9 j = 1,и регрессии Л", на ёк (t -у), У=1, q. По первым из них получаем начальные оценки наименьших квадратов для параметров aJ9 т.е. aj9 j = 1,р9 а по вторым — оценки bj для bJ9 7=1,q. Соответственно оценками полиномов a(z)9 b(z) служат

a(z) = l-£a,V,

7=1 7=0

и с помощью оцененных полиномов получаем оценку для инноваций

st = b~l(L)a(L)xt9

на основании которой строим уточненную оценку для дисперсии инноваций

1 Т 1 t =

При этом предполагается, что сами инновации, если известны точно коэффициенты ARMA модели, можно найти по формуле st = b~x(L)a(L)xt9 что соответствует обратимости этой модели.

В качестве оценок для р09 q0 берется пара значений (р9 q)9 при которой минимизируется величина

SIC(^?) = ln^?+(p + 9)^.

Существенно, что SIC (5^) — возрастающая функция от р и q9 когда p>p09q>q09 что ведет к состоятельности оценок (р9 q).

Оценивание коэффициентов модели

После того как произведена идентификация (стационарной) модели ARMA, т.е. на основании имеющихся наблюдений принято решение о значениях параметров р9 q модели ARMA(p, q)9 порождающей данные, переходят к этапу оценивания коэффициентов модели. На этом этапе обычно используется метод максимального правдоподобия, который в случае нормальности инноваций сводится к методу наименьших квадратов. За исключением некоторых наиболее простых случаев (например, модели AR(1)), эта задача решается итерационными методами, требующими задания некоторых начальных (стартовых) значений параметров, которые затем последовательно уточняются.

В качестве таких начальных значений можно использовать предварительные оценки, полученные на первом этапе. Начальные значения можно найти, приравнивая неизвестные истинные значения автокорреляций р(к) значениям г(к) выборочной автокорреляционной функции и используя функциональную связь между значениями р(к) и значениями коэффициентов модели. Например, если оценивается модель AR(p), то коэффициенты al9 а2, ар определяются из системы первых р уравнений Юла — Уокера

р

р(к) = YjajP(k~-J)> к = 19...9р9

7 = 1

в которые вместо неизвестных значений р()9pip) автокорреляций подставляются наблюдаемые (вычисляемые по реализации ряда) значения г(1),..., г(р) выборочных автокорреляций.

При оценивании моделей с MA(q) составляющей (q > 0) существенным оказывается условие обратимости, сформулированное выше. Покажем это на примере МА(1) модели

Xt-/i = et+bxet_X9 / = 1,...,Г.

Имея наблюдаемые значения хх, хТ, последовательно выразим єІ9 єт через эти значения и (ненаблюдаемое) значение є0:

єх =ХХ-р-Ьє0,

є2 = Х2 -р -Ьєх = Х2 р -Ь(ХХ -р -Ьє0) = (Х2 -р) -Ь(ХХ р) + Ь2є0,

єт = Хт -р-Ьєт_х = (Хх -р)-b(XT_x -р) + Ь2(ХТ_2 -р)-...+ + (-iy->bT-Xl-M) + (-fbTs0.

Максимизация (по Ь) условной функции правдоподобия, соответствующей наблюдаемым значениям xl9 хп при фиксированном значении є0, равносильна минимизации суммы квадратов

Q(b) = £f +є\%+.+

которая является нелинейной функцией от Ь. Для поиска минимума этой суммы квадратов приходится использовать численные итерационные методы оптимизации, которые, в свою очередь, требуют задания начального (стартового) значения параметра Ь. Как уже говорилось, такое стартовое значение может быть получено на этапе идентификации модели. Однако полученное в итоге итераций оптимальное значение Ь зависит от неизвестного значения є09 что затрудняет интерпретацию результатов. Задача интерпретации облегчается, если выполнено условие обратимости Ь < 1, и при этом значение Ь существенно меньше 1.

Действительно, при выполнении этого условия можно просто положить є0 = 0. Эффект от такой замены истинного значения є0 на нулевое быстро убывает, так что сумма квадратов, получаемая в предположении є0 = 0, может служить хорошей аппроксимацией для суммы, получаемой при истинном значении є0, при достаточно большом количестве наблюдений. Те же аргументы пригодны и для модели MA(q) с q > 1: в этом случае можно положить є0 = є_х = ... = £-q+i = 0. Для получения более точной аппроксимации в пакетах статистических программ (в том числе и в EViews) предусмотрена процедура backcasting, в которой процесс итераций включает также оценивание значений є0 = є_х = ... = є_д+х путем построения для них обратного прогноза.

Если в результате оценивания получена модель, в которой условие обратимости не выполняется, рекомендуется повторить процедуру оценивания с использованием другого набора начальных значений.

Более подробное изложение процедур оценивания стационарных ARMA моделей методом максимального правдоподобия можно найти, например, в (Hamilton, 1994, р. 117—151). Там же можно прочитать о том, каким образом вычисляются приближения для стандартных ошибок оценок коэффициентов этих моделей, которые можно использовать при большом количестве наблюдений обычным образом.

В заключение сделаем одно важное замечание.

Пусть имеем стационарную AR(p) модель

a(L)Xt = S + sr

Ранее говорилось о том, что в этом случае математическое ожидание ju процесса Xt связано с константой 8 соотношением

д

М= >

-ах а2-...ар

При этом можно сначала оценить коэффициенты аХ9 а29 ар и S, применяя обычный метод наименьших квадратов к модели

Xt = 8 + axXt_x + a2Xt_2 +... + apXt_p + et,

а затем, используя полученные оценки dl9 ар и S9 получить оценку для ju в виде:

Однако можно поступить иначе, как это предусмотрено, например, в пакете EViews. Можно записать ту же модель в виде:

Xt = ju(-ax -a2-...-ap) + axXt_x + a2Xt_2 +... + apXt_p + et

и одновременно оценивать и ах, а2, ар, и /и. Такая процедура теоретически более эффективна. Однако в такой форме модель оказывается нелинейной по параметрам, и это обстоятельство, как и при оценивании МА моделей, требует применения нелинейного метода наименьших квадратов (NLLS — nonlinear least squares) и численных итерационных методов оптимизации.

ПРИМЕР 7.2.2

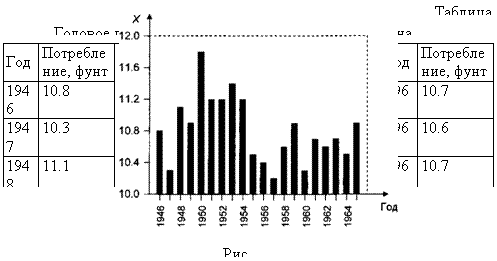Рассмотрим ряд данных о годовом потреблении рыбных продуктов в США (на душу населения, в фунтах). Статистические данные приведены в табл. 7.7, график ряда — на рис. 7.24.

Ориентируясь на указанные ранее приближенные критерии, прежде всего 2 2

найдем значение —j= = -7= = 0.447. Из полосы ±0.447 не выходит ни одна л/Т V20

из выборочных автокорреляций и частных автокорреляций. Поэтому исходя из этих критериев не должна отвергаться гипотеза о том, что наблюдаемый ряд порождается моделью МА(0)

Х0=;и + єг

В то же время если ориентироваться на критерий Люнга — Бокса, то пик ACF на лаге 1 является статистически значимым. Это означает, что в качестве потенциальных моделей порождения данных можно предварительно рассматривать модели AR(1) и МА(1). Таким образом, здесь сталкиваемся с конфликтной ситуацией: статистические выводы, получаемые при использовании разных критериев, не соответствуют друг другу. Подобная ситуация не является чем-то исключительным и достаточно часто встречается при идентификации модели, порождающей наблюдаемый ряд, тем более что используемые критерии — асимптотические, тогда как обычно в распоряжении исследователя имеется не слишком большое количество наблюдений. ■

Последнее обстоятельство связано в значительной степени с тем, что для многих экономических рядов периоды, на которых порождающая ряд модель может считаться стационарной, обычно непродолжительны из-за изменения общей экономической обстановки, в которой эволюционирует рассматриваемый ряд. Это соображение можно легко проиллюстрировать на примере того же самого ряда данных о потреблении рыбных продуктов в США, если привлечь дополнительно статистические данные за период с 1940 по 1945 г. (годы Второй мировой войны). Эволюция ряда на расширенном периоде с 1940 по 1965 г. представлена на рис. 7.25.

Провал траектории ряда в 1942—1944 гг. не позволяет трактовать этот ряд как стационарный на всем периоде с 1940 по 1965 г. Поэтому продолжим далее рассматривать значения ряда только на послевоенном периоде — с 1946 по 1965 г.

X

12 4

11

10

гтттттттттттттттттттт

OCN^t<OOOOCN^<DOOO

СМ

Год

Рис. 7.25

Если остановиться на модели AR(1), то для нее, как мы знаем, р() = ах. Поэтому, приравняв неизвестное значение р() значению г() = 0.429, получим предварительную оценку для неизвестного значения ах. В то же время, непосредственно оценив модель AR(1) с ненулевым математическим ожиданием нелинейным методом наименьших квадратов, получим следующие результаты (табл. 7.8).

Таблица 7.8

В данной ситуации уточненная оценка практически совпадает с предварительной оценкой для ах.

Если остановиться на модели МА(1), то в ней р(1) =

+ъ;

. Приравнива-

ние неизвестного значения р(1) значению г(1) = 0.429 приводит к уравнению

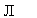
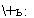= 0.429. Корни последнего уравнения равны 0.567 и 1.704. Первый

Объясняемая переменная X

Backcast: 1945

корень соответствует обратимой МА(1) модели, второй корень — необратимой МА(1) модели. Уточненное оценивание МА(1) модели с использованием обратного прогноза (backcasting) дает следующие результаты (табл. 7.9).

В этом случае уточненное значение коэффициента Ьх существенно отличается от предварительной оценки этого коэффициента. Отметим также большое отличие Р-значений для tи F-статистик в отношении значимости коэффициента Ьх. Это можно объяснить тем, что величина стандартной ошибки вычисляется согласно асимптотической процедуре, тогда как в нашем распоряжении имеется лишь 20 наблюдений.

Если не производить обратного прогнозирования значения инновации для 1945 г., то результаты получаются близкими (табл. 7.10).

Объясняемая переменная X

Method: Least Squares; Sample (adjusted): 1946 1965; Included observations: 20 after adjusting endpoints; Convergence achieved after 24 iterations; Backcast: OFF

Диагностика оцененной модели

После выбора типа модели и оценивания ее коэффициентов производится диагностика оцененной модели, т.е. выяснение того, насколько хорошо модель соответствует данным наблюдений (адекватна данным наблюдений). Это — третий этап процедуры подбора модели.

Для диагностики можно использовать целый ряд различных статистических процедур, которые направлены в основном на проверку гипотезы Я0 о том, что в модели, порождающей наблюдения, последовательность et действительно образует процесс белого шума.

Пусть на этапе идентификации остановили свой выбор на модели ARMA(p, q)

a(L)Xt=b(L)sn

т.е.

Xt = axXt_x + a2Xt_2 +... + apXt_p +st+ bxst_x +... + bqst_q, и на втором этапе оценили ее как

a(L)Xt=b(L)sn

где

a(L) = l-axL-...-apLp,

b(L) = l + bxL + ... + bqLq. Если MA составляющая модели ARMA(p, q) обратима, то

и оценки для st теоретически можно получить заменой a(L) и b(L) на a(L) и b(L) соответственно:

* _ a(L)

st —— Л .

b(L)

На практике, конечно, эту формулу можно использовать лишь частично, поскольку бесконечный ряд в правой части приходится обрывать из-за наличия только конечного количества наблюдений.

При большом количестве наблюдений поведение st должно имитировать поведение самих єг Следовательно, если ошибки st образуют процесс белого шума, то остатки должны имитировать процесс белого шума.

Основываясь на этом соображении, Бартлетт {Bartlett, 1946) и Бокс и Пирс (см. (Box, Pierce, 1970)) предложили исследовать статистическую значимость выборочных автокорреляций для ряда инноваций st:

Т-к

ге{к) = ^-Т

t =

и суммы их квадратов

м

Qbp = Т^Гє(к) ((^-статистика Бокса — Пирса).

к=

Если модель правильно специфицирована, то QBP имеет распределение, которое близко к распределению J 2(Мp-q) при условии, что Г и М велики, а отношение М/Гмало. Гипотеза адекватности подобранной модели отвергается, если

Qbp> ХІ95ІМ-Р-Я)-Однако впоследствии было замечено, что при конечных Т распределение статистики QBP может существенно отличаться от распределения j2(Mр q). Используя результаты Люнга и Бокса, можно показать, что

E(QBP)*(M-p-q) 2Г + 2 .

М(М + 5)

Следовательно, если отношение — существенно, то использова2Т + 2

ние x2W~p q) приближения не является оправданным.

Люнг и Бокс предложили два способа преодоления проблемы смещения. Первый — прямой метод — состоит в использовании приближения

Qbp*xE(Qbp)

где для E(QBP) используется указанное выше выражение (модифицированный

критерий Бокса — Кокса).

сто — берется ———. Это приводит к (^-статистике Люнга — Бокса

Второй способ учитывает более точное выражение для D(rs(k)) — вме1 ^ Т-к

— берется —

Т Т + 2Т

М 2

QLB=T(T + 2)£ £

к=1Т-к

которая имеет то же асимптотическое распределение хМ р q), что и QBP, но зато при конечных Г распределение статистики QBP гораздо ближе к \%2(Мр q чем распределение статистики QBP. При этом качество приближения ухудшается, если значения параметров находятся вблизи границы стационарности или обратимости модели; особенно это заметно при малых М. Заметим: хотя первоначально вывод асимптотического распределения статистики Люнга — Бокса производился в предположении, что et — гауссовский белый шум, в дальнейшем было установлено, что этот критерий достаточно устойчив к отклонениям распределения et от нормального. Важно только, чтобы была конечной дисперсия D(et). Последнее условие часто нарушается для рядов, описывающих эволюцию быстро изменяющихся финансовых показателей (цен на акции, биржевых индексов, обменных курсов). Для таких рядов et обычно имеет распределение с тяжелыми «хвостами» (heavy-tailed distribution), т.е. достаточно часто наблюдаются большие по абсолютной величине значения ег В связи с этим для описания таких рядов необходимы более сложные модели.

В пакете EViews в распечатке результатов оценивания моделей ARMA рядом с коррелограммой ряда остатков приводятся Р-значения для наблюдаемых значений g-статистики Люнга — Бокса.

Для рассмотренных выше моделей AR(1) и МА(1) коррелограммы рядов остатков имеют следующий вид.

В обоих случаях все Р-значения для статистики QBP больше 0.05, так что гипотеза о том, что в специфицированных моделях составляющие et образуют процесс белого шума, не отвергается. Заметим также, что в обоих случаях не отвергается гипотеза нормальности распределения et Р-значения критерия Харке — Бера равны соответственно 0.480 и 0.608. Об оправданности применения последнего критерия при анализе временных рядов будет сказано ниже.

Проверка предположения о нормальности. Многие статистические процедуры, используемые при анализе временных рядов, опираются на предположение гауссовости (нормальности) анализируемого ряда. Последнее означает, что для любого набора tl9 tn случайные величины Xt9 Xt

имеют совместное нормальное распределение.

Имея в распоряжении одну-единственную реализацию временного ряда, невозможно проверить справедливость такого утверждения. В то же время можно проверить гипотезу о нормальности одномерного (маргинального) распределения стационарного временного ряда. Соответствующая процедура предложена в работе Ломницкого (Lomnicki, 1961).

Пусть

1 t=

_ т3 _ т4

Щ т2

В указанной работе было доказано, что если Xt — стационарный гауссов-ский временной ряд, то при больших Т статистики Gx и G2 имеют приближенно нормальные распределения с нулевыми математическими ожиданиями и дисперсиями

W,) = f |>3(*), Z>(G2) = ^f>4(*).

Оценить эти дисперсии можно путем замены бесконечных сумм степеней автокорреляций р(к) конечными суммами степеней выборочных автокорреляций г (к). Используя такие оценки D(G{)9 D(G2)9 получим статистики

Г* - Gl Г* G2

д/ОД) JD(G2)

которые при гипотезе нормальности имеют распределения, аппроксимируемые стандартным нормальным распределением. Поскольку последние статистики еще и асимптотически независимы, то при Т -> оо

(G;)2+(G2*)2*j2(2).

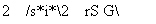распределением хи-квадрат в пакете EViews в статистике критерия вместо множителя Т используется множитель (Т К), где К — количество коэффициентов, оцениваемых при построении модели исследуемого ряда.

Правда, здесь мы не заметили еще одного подводного камня. Мы предполагали неявно, что остатки берутся как результат оценивания правильно идентифицированной модели. Как будет влиять на свойства критерия неправильное определение порядка модели?

При больших Т критерий Шварца достаточно надежно определяет порядок (р, q) модели ARMA, так что проверка нормальности инноваций по модели, выбранной критерием Шварца, асимптотически равносильна проверке нормальности инноваций по правильно идентифицированной модели.

На третьем шаге производят также проверку выбранной модели на оптимальность, при этом имеется в виду, что «более сложные» модели не должны существенно отличаться от подобранной модели. Точнее говоря, при увеличении порядка модели оценки коэффициентов при добавленных составляющих должны быть статистически незначимыми, а оценки коэффициентов при сохраняемых составляющих должны изменяться не очень существенно.

J Замечание 7.2.1. При построении статистики Харке — Бера для проверки нормальности инноваций в модели ARMA существенным является центрирование остатков, полученных в результате оценивания модели, т.е. вычитание из каждого остатка et среднего et всех полученных остатков.

При оценивании модели линейной регрессии методом наименьших квадратов сумма полученных остатков равна 0, так что остатки автоматически являются центрированными. Поскольку же при оценивании ARMA моделей приходится привлекать метод максимального правдоподобия, получаемые остатки необязательно являются центрированными, и надо позаботиться об их центрировании. В противном случае статистика Харке — Бера уже не имеет асимптотического распределения j2(2) (см. (Yu, 2007)).

ПРИМЕР 7.2.3

Обратившись опять к результатам оценивания МА(1) и AR(1) моделей для данных о потреблении рыбных продуктов в США, заметим, что гипотеза Н0 : ах = 0 в AR(1) модели и гипотеза Н0 : b{ = 0 в МА(1) модели не отвергаются. Это означает, что обе эти модели могут быть редуцированы к модели МА(0)

Xt = ju + sr

При оценивании последней получим результаты, приведенные в табл. 7.11. Однако оцененная коррелограмма для этой модели уже была приведена выше (в примере 7.1.2) и именно она дала повод рассматривать в качестве

возможных кандидатур модели AR(1) и МА(1). При этом, решая вопрос о статистической значимости р() и ppart(l\% мы опирались на асимптотические результаты, хотя имели в распоряжении лишь небольшое количество наблюдений, и это может быть причиной несогласованности полученных выводов.

Впрочем, можно воспользоваться и точным критерием, основанным на статистике Дарбина — Уотсона. Поскольку в последней модели нет никаких объясняющих переменных, кроме константы, можно получить таблицы непосредственно для критических значений этой статистики, а не для границ, между которыми заключены эти критические значения. Соответствующие критические значения приведены в (Sargan, Bhargava, 1983). В частности, для уровня значимости 0.05 и Т= 21 критическое значение равно 1.069. Ориентируясь на него, мы не отвергаем гипотезу о том, что наблюдаемые данные порождены процессом МА(0).

Сравним оцененные модели МА(0), МА(1) и AR(1) по критериям Акаике и Шварца (табл. 7.12).

Предпочтительной по критерию Акаике является модель AR(1), тогда как с точки зрения критерия Шварца более предпочтительна модель МА(0). Такое положение в практическом анализе временных рядов возникает достаточно часто: если критерии Акаике и Шварца выбирают разные модели, то критерий Акаике выбирает модель более высокого порядка. ■

ПРИМЕР 7.2.4

Обратимся к приведенной в примере 7.2.1 реализации процесса авторегрессии второго порядка= 2Xt_x 036Xt_2 + єг Используя выборочную кор-релограмму, построенную по этой реализации, мы (правильно) идентифицировали порядок этого процесса. Среди AR моделей порядков 4, 3, 2 и 1 оба критерия — АІС и SIC — также выбрали модель второго порядка. Оценивание модели с ненулевым математическим ожиданием нелинейным методом наименьших квадратов приводит к следующим результатам (табл. 7.13).

Все Р-значения для статистики QBP намного больше 0.05, так что гипотеза о том, что в специфицированной модели составляющие st образуют процесс белого шума, не отвергается. Не отвергается также и гипотеза нормальности st (Р-значение в критерии Харке — Бера равно 0.616). Вместе с тем оценка математического ожидания процесса Xt статистически незначима, что позволяет не отвергать гипотезу о нулевом математическом ожидании AR(2) процесса. Оценив модель с нулевым математическим ожиданием, получим результаты, приведенные в табл. 7.14.

Исследуем последнюю модель на оптимальность в указанном выше смысле. С этой целью приведем коэффициенты оцененных AR(2), AR(3) и AR(4) моделей и Р-значения для тех коэффициентов двух последних моделей, которые являются «лишними» с точки зрения «оптимальной» модели AR(2) (табл. 7.15).

Эта таблица показывает, что в моделях с неоправданно высоким порядком «лишние» коэффициенты оказались статистически незначимыми, а коэффициенты при переменных, включенных в «оптимальную» модель, практически не изменяются при изменении порядка модели. Именно это и характеризует подобранную модель AR(2) как оптимальную.

Интересно, наконец, обратить внимание еще на одно обстоятельство. Как было уже отмечено ранее, в теоретической модели AR(2), по которой строилась исследуемая реализация, уравнение a(z) = 0, т.е. 1 1.2z + 0.36z2 = 0,

имеет двойной корень z = ^-«1.67. Этот корень больше 1, что обеспечивает

стационарность процесса, порождаемого такой моделью. В то же время для оптимальной модели, полученной в результате подбора, соответствующее уравнение имеет корни, обратные величинам, указанным в последней строке распечатки результатов оценивания этой модели. Указанные в этой строке величины равны 0.63 ± 0.05/, так что сами корни равны z 1.58 ± 0.125/. Хотя эти корни, конечно, отличаются от (двойного) корня уравнения a(z) = 0 в теоретической модели, тем не менее оба они больше 1 по абсолютной величине, а значит, подобранная AR(2) модель также является стационарной. ■

КОНТРОЛЬНЫЕ ВОПРОСЫ

Какие три этапа используются при подборе стационарной модели ARMA для ряда наблюдений? В чем состоят эти этапы?

Что является отправной точкой для идентификации стационарной модели ARMA?

Как можно идентифицировать процесс авторегрессии и его порядок?

Как можно идентифицировать процесс скользящего среднего и его порядок?

Как можно идентифицировать сезонные процессы авторегрессии и скользящего среднего?

Каким образом производится оценивание коэффициентов модели, идентифицированной как AR(p)?

Каким образом производится оценивание коэффициентов модели, идентифицированной как МА(#)?

Какие статистические процедуры применяются для диагностики подобранной модели?