Раздел 6 методология векторных авторегрессий тема 6.1 прогнозирование по модели векторной авторегрессии, проверка наличия причинности по грейнджеру для двух рядов и более
Раздел 6 методология векторных авторегрессий тема 6.1 прогнозирование по модели векторной авторегрессии, проверка наличия причинности по грейнджеру для двух рядов и более
В рамках моделей векторных авторегрессий (VAR) довольно часто производят проверку гипотезы о том, что некоторая из переменных, образующих VAR, является причиной по Грейнджеру ((7-причиной) для некоторой другой переменной, входящей в эту же VAR.
Рассмотрим пару переменных (два временных ряда) xtnyt. Пусть:
— информационное множество, содержащее значения хТ9 хт_ l9 Q/ — информационное множество, содержащее значения уТ9 ут_ l9 ...; Qf,y — объединение этих двух множеств;
у T+h | Q = E(yT+h IQ) — оптимальный прогноз ряда yt на h шагов вперед относительно информационного множества Q, где в качестве Q могут выступать информационные множестваQj или Qjy.
Говорят, что переменная х не является причиной по Грейнджеру для переменной j (х is Granger-noncausal for у), если
УТ+И -(yT+h П£) < ЕyT+h -(yT+h ПХТ'У)
для h = 1, 2,
так что дополнительная информация о значениях хТ9 xT_l9 ... не улучшает оптимальный прогноз для yT+h — для его построения достаточно использовать только значенияуТ9ут_l9 ... . Если же такая информация улучшает оптимальный прогноз, то переменная х является причиной по Грейнджеру для переменной j (х Granger-causes у).
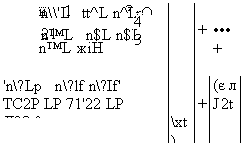
Пусть поведение переменных х и у описывается двумерной VAR
C2J ҐгЛ
71 \ "12 п2 п22 J
fx
+ п,
ҐХ Л Vl
+ ■■■ +
t-p
22 J
4" 4рЛ
(p) -(p)
П2
fx Л
(с
62tJ
C2J
y*-pj
62tJ
Случайные величины єХп s2t образуют случайный вектор et = (єХп є2,)Т9 компоненты которого не коррелированы по времени и не коррелированы с запаздывающими значениями переменных: et — вектор инноваций (обновлений) относительно информационного множества
0^^м,хм,Л_2,х,-2,...). Указанную модель можно записать в виде:
X, = СХ + tfftVl + • • • + Я\-р + ПпУі+ • • • + *АіУі-р + єь > У<=С2+ Л^Х,-! + ... + 7t^Xt_p + 7T{£yt_x + ... + n{£yt_p + €2t.
Отсюда видно, что оптимальные прогнозы переменных х„ yt на один или несколько шагов вперед задаются формулами:
*7+1
Q
(!>1
r(P)
і + п|}х, + ... + + ЯпУі + • • • + *гУі-р+\>
 |
C2J
"11 П2
О л-(1) , и п22 j
ґх Л xtкУі-w
+ ••• +
О Ttgj
fx } Уі-р)
• у не является G-причиной для х, если 7ГІ2 = ••• = = 0, т.е. если матрицы коэффициентов П. являются нижними треугольными:
| = V | о Л | (х Л xt- | л\ | 0 ) | fx } | (г Л | |||||
| + | л22 ) | + ••• + | + | ||||||||
| C2j | .л2 | *£) | KS2t) |
Если рассматриваемая двумерная VAR стабильна1, то для проверки гипотезы Н0: «у не является G-причиной для х» достаточно произвести OLS-оце-нивание модели
х, = сх + axxt_x +... + apxt_p + pxyt.x +... + /3pyt_p + ut
(с (2p + 1) коэффициентами) и, используя F-критерий, проверить гипотезу
Я0: рх=... = рр=0.
При нулевой гипотезе асимптотически статистика критерия имеет распределение, близкое к F-распределению F(p, Т-2р-). Асимптотически эквивалентным этому критерию является критерий, основанный на статистике pF, которая при нулевой гипотезе имеет асимптотическое распределение \%2(р). Соответственно для проверки гипотезы Н0: «х не является G-причиной для у» достаточно произвести ttLS-оценивание модели
yt = сх + axxt_x +... + apxt_p + pxyt_x +... + fipyt_p + ut
(с (2p + 1) коэффициентами) и, используя F-критерий, проверить гипотезу
Н0:ах=... = ар=0.
J Замечание 6.1.1. Результаты практического применения любого из тестов на существование причинности по Грейнджеру чрезвычайно чувствительны к выбору глубины запаздываний р ик методам, предусмотренным для случая потенциально нестационарных рядов.
Причинность по Грейнджеру не следует истолковывать как причинность в философском смысле! Это всего лишь попытка спецификации необходимого условия для причинной связи. Причинность по Грейнджеру предоставляет возможность улучшить качество прогнозов одной из переменных с привлечением информации о прошлых значениях другой переменной, в дополнение к информации о прошлых значениях самой переменной. Интерпретация причинности по Грейнджеру как необходимого условия для причинной связи
наталкивается на следующее затруднение: отношение х—^—»>> (переменная
х является причиной для переменной;;) не является транзитивным. Например,
См. разд. 8 ч. 2 данного учебника.
возможно, что z—^—>jc и х—^—>у, но переменная z не является G-причиной для переменной;;.
Если в модели для пары переменных xt и yt обе переменные реагируют на изменение некоторой третьей переменной, не включенной в модель, то Грейнджер-причинность между переменными xt uyt может обнаружиться и при отсутствии G-причинного влияния одной из этих переменных на другую.
В связи с последним обстоятельством рассмотрим трехмерную VAR, описывающую совместную динамику переменных хпyt и zt
 |
Л, Л
xt)
Последнее соотношение можно записать в форме:
 |
съ)
zt
xt J
или
Vc3 7
7tn{L) лп{Ь) 7tn{L)
я2хЩ 7i22{L) я1Ъ(Ь) *зі(L) пъ2 (L) яъъЩ
xtJ
r є Л
°2f
Непосредственный перенос условия G-причинности х >у для VAR
-»z И Zс двумя переменными на VAR с тремя переменными приводит к следующему условию отсутствия такой связи: 7tn(L) = 0. Но если остальные элементы
матрицы отличны от 0, то х->у, т.е. такое определение
G-причинности не является транзитивным в системах с тремя переменными и более.
Пусть, например,
yt~c+ *\Уі+ n2Zt+
Zj — C2 л22 Zt— Л23Хі— £2t*
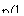
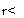 X, -C3 +7t^2zt+ Л3з'*(-1 +£2f
X, -C3 +7t^2zt+ Л3з'*(-1 +£2f
Запаздывания переменной х не входят непосредственно в правую часть уравнения для у (7т[3 = 0). Однако zM = с2 + n22zt_2 + nrixt-2 + ^ 2,м» так что
Л = С1 + П\Уі+ * U (С2 + Т&Ч-г + *2зЧ-2 + *2,/-1)+ єи =
Чтобы исключить влияние запаздываний переменной х на >>, надо положить (дОПОЛНИТеЛЬНО К УСЛОВИЮ л3 = 0) или п2 = 0, или я2Ъ(Ь) = 0:
7Tl2(L) = 0 и 7Tn(L) = 0 (случай 1)
7rl3(L) = 0 и 7r23(L) = 0 (случай 2).
В первом случае в выражение для yt входят только прошлые значения самой этой переменной:
Щ1) =
*n(L) яІЗ(£)ї
?г(1) пъг(Р) ХзЛ1).
0 0 *2і(£) ^22 (L) *23 СО *зі (L) ^32 W *зз(Д
Во втором случае в выражение для у, входят еще и прошлые значения переменной z. Однако выражения для последних не содержат прошлых значений переменной х, так что и в этом случае прошлые значения переменной х не входят в выражение для у,:
П(1) =
яг(1) яіз(£)" я-21(І) л-22(І) л-23(І)
^з,(І) л-32(І) /r33(Z,)
4,(0 *12(І) 0 ^
^31(І) я32Щ я„{Ь)
В обоих случаях матрица ЩЬ) является блочно-треугольной с двумя блоками размеров (2 х 2) и (1 х 1).
Если рассматривать пару переменных z и у, то как непосредственное, так и опосредованное (через посредство переменной х) влияние переменной у на переменную z исключается при выполнении условий:
7r3i(L) = 0 и 7Г21(Ь)-0 (случай 3)
либо условий:
я-21(1) = 0 и 7т2Ъ{Ь) = 0 (случай 4). В случае 3 матрица ЩЬ) имеет вид:
fJtn(L) яп(Ь) щ3(Ь)Л
0 к22(1) я2Ъ(Ь) 0 щ2{Ь) жъъ{Ь)/
в случае 4:
U{L) =
яі,(і) о
tf31(I)
Л"12(І)
л-22(І) rr32(L)
о
л-33(І)
/г12(1) о
В последней ситуации матрица Щ/,) не является блочно-треугольной, но если поставить переменную х на второе место, а переменную z — на третье место, то матрица ЩЬ) примет блочно-треугольную форму:
Щ1) =
/г23(1) л-33(1)
/г21(1) о
nn(L) пхъ(1^
В подобных случаях говорят о блочной экзогенности (block exogeneity) одной группы переменных (или некоторой переменной) в отношении другой группы переменных (или другой переменной). Блочная экзоген-ность означает, что запаздывающие значения второй группы переменных не входят в уравнения для переменных первой группы.
В рассмотренных выше четырех ситуациях (при выполнении соответствующих четырех пар условий) получаем:
в случае 1: переменная у блочно экзогенна в отношении переменных z и х (переменные z и х не участвуют в ее формировании);
в случае 2: пара (у, z) блочно экзогенна в отношении переменной х (переменная х не участвует в формировании у и z);
в случае 3: пара (z, х) блочно экзогенна в отношении переменной>> (переменная у не участвует в формировании х и z);
в случае 4: переменнаяz блочно экзогенна в отношении переменных у их (переменныеу их не участвуют в ее формировании).
Пусть теперь имеется N переменных (N временных рядов) у1п уЪ9 yNt9 составляющих векторный ряд^,^ = (уи, г )Г (верхний индекс Г означает транспонирование вектора). Рассмотрим разбиение вектора^, на две части:
где yjl) = (yu, Пусть:
yt =
„(2)
КУі J 9yKt)T9 1<NX<N.
(i)
Q<2)
информационное множество, содержащее значения yiT9 yit т_ x, (/ = 1,Nx) первой группы переменных;
информационное множество, содержащее значения yiT, yt> т_ х, (i = Nx + 1, N) второй группы переменных;
Q^1,2) — объединение этих двух множеств;
уиT+h Q = E(yt T+h Q) — оптимальный прогноз і-й переменной первой группы на h шагов вперед относительно информационного множества Q, где в качестве Q могут выступать информационные множества Q <1} или Q <U).
Говорят, что переменные второй группы не являются Грейнджер-при-чиной для переменных первой группы, если
У,,т+н -(Лг+М0) <EyUT+h-(yUT+h «>V)
для h = 1, 2, ..
так что дополнительная информация о значениях переменных второй группы не улучшает оптимальный прогноз переменных первой группы — для его построения достаточно использовать только значения yiT9 yif т_ х ,...(/= 1, ..., Nx) первой группы переменных. Если же такая информация улучшает оптимальный прогноз, то переменные второй группы являются причиной по Грейнджеру для переменных первой группы.
Пусть динамика (Nx 1)-вектора;;, представлена гауссовской VAR(p):
yt=c + Uxyt_x +... + Upyt_p + єп et~ Ltd. N(0, Ї),
и гипотеза состоит в том, что переменные второй группы не являются Грейнджер-причиной для /-й переменной первой группы (/' = 1,2, Nx). Для проверки этого предположения оценивается уравнение
и проверяется гипотеза
но: Кі =л2і = ... = Ярі=0.
Если рассматриваемая VAR стабильна, то использование F-статистики для проверки этой гипотезы асимптотически оправданно. Проблемы возникают в случае нестабильной VAR.
Если рассмотреть в качестве нулевой гипотезу
Н0:ЛХІ=Л2і=... = Лрі=0, i = l,2,...,Nl9
1 См. разд. 8 ч. 2 данного учебника.
охватывающую все Nx уравнений первой группы, то такая гипотеза соответствует блочной экзогенности первой группы переменных в отношении второй группы переменных. Если эта гипотеза выполняется, то в порождении переменных первой группы не участвуют переменные второй группы. Соответственно N2 уравнений второй группы образуют открытую VAR1, которую можно рассматривать самостоятельно.
Последняя гипотеза накладывает Nxp ограничений на коэффициенты VAR(p) для N = NY + N2 переменных и при Nx > 1 имеет перекрестный характер, затрагивая коэффициенты сразу нескольких уравнений (точнее, коэффициенты Nx уравнений). Проверить эту гипотезу можно, применяя критерий отношения правдоподобий (/,7?-критерий), статистика которого равна:
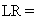 UNRESTR IrESTR
UNRESTR IrESTR
) = T(ln
* RESTR
-In
"unrestr
 unrestr'
unrestr'
Irestr
HI —
логарифм максимума функции правдоподобия при оценивании VAR(p) без ограничений на коэффициенты; логарифм максимума функции правдоподобия при оценивании VAR(p) с ограничениями на коэффициенты, соответствующими проверяемой гипотезе;
определитель оцененной ковариационной матрицы инноваций, вычисляемой двумя разными способами:
= det
1
или
= det
1
Т t
Статистика LR имеет асимптотическое распределение хи-квадрат с числом степеней свободы, равным количеству зануляемых коэффициентов.
Нестационарные VAR
Пусть динамика (N х 1)-вектора>>, представлена моделью VAR(p): yt=a + Uxyt_x +... + Upyt_p + €t, st ~ u.d.9 E(st) = 0, Cov(st) = I. Последнее представление можно записать следующим образом: yt ~ пі^-і ~ • • •" ПрУі-Р =а + єп
или
Yl(L)yt =а + єп
где
U(L) = IN-UxL-..^UpLp.
Во второй части учебника (разд. 8, тема 8.2) уже говорилось о том, что условие стабильности такой VAR состоит в следующем:
Все корни алгебраического уравнения det U(z) = 0 лежат за пределами единичного круга на комплексной плоскости (т.е. модули всех этих корней больше 1).
Замечание 6.1.2
Если VAR рассматривается на всей оси времени, то из стабильности VAR вытекает ее стационарность как векторного процесса (стационарность в широком смысле).
Если VAR рассматривается только с некоторого момента времени при заданных начальных условиях, то из стабильности VAR вытекает ее асимптотическая стационарность.
Существуют (не рассматриваемые обычно) стационарные модели VAR, для которых условие стабильности не выполнено.
Если VAR, рассматриваемая на всей оси времени, нестационарна, то она нестабильна.
Пусть компоненты вектора уп динамика которого представлена моделью VAR(p), являются Д1)-рядами (интегрированными рядами порядка 1), так что ряды их приращений (ряды разностей) являются стационарными временными рядами, а сама VAR нестабильна. Стандартную форму векторной авторегрессии порядка р
yt=a + Ylxyt_x +... + Upyt_p + et (6.1)
можно переписать в виде:
yt = £ Лум +... + Cp_xAyt_p+x +а + pyt_x + et, (6.2)
где /7 = П1+... + П/?,
^ =-(П,+1 +П,+2 +... + Пр) для s= 1, 2,
Некоинтегрированная VAR
Если р = IN, то компоненты yt не коинтегрированы, и модель принимает форму векторной авторегрессии VAR(p 1) в разностях:
4У, =САУі-х +-+ Ср-АУі-р+і +<* + єг (6.3)
При оценивании статистической модели (6.2) независимо от того, а = О
или а * О в DGP, совместное распределение оценок матричных коэффициентов £і, £ х является асимптотически нормальным, причем это асимптотическое распределение точно такое же, как и для совместного распределения
оценок матричных коэффициентов £ х в модели (6.3). Соответственно
для проверки гипотез об этих коэффициентах (как в рамках уравнения (6.2), так и в рамках уравнения (6.3)) можно использовать (асимптотически) стандартные tи F-критерии или статистику qF ~ хч)> гДе Ч — количество (линейно независимых) линейных ограничений на элементы матриц ^, ..., С,р_х,
Непосредственно в рамках уравнения (6.1) возможно использование стандартных тестов для проверки гипотезы
H0:DGP = VAR(p0)9 Po>h
против альтернативы
HA:DGP = VAR(p)9 р>р0,
с целью выбора оптимальной глубины запаздываний. Но, например, F-крите-рий для проверки гипотез о значении суммы П{ + ... +Пр (т.е. о значении р) в этой ситуации неприменим: оценка для этой суммы имеет нестандартное распределение. Кроме того, статистики критериев для проверки на причинность по Грейнджеру отдельных переменных или подгруппы переменных (компоненту) не имеют обычных асимптотических распределений. Поясним этот факт.
Пусть компоненты вектора yt являются /(І)-рядами (интегрированными рядами порядка 1), так что ряды их приращений (ряды разностей) являются стационарными. Опять рассмотрим разбиение вектора yt на две подгруппы, включающие соответственно Nx и N2 = N N{ переменных, и пусть гипотеза Н0 состоит в том, что переменные второй группы не являются Грейнджер-причиной для переменной yit первой группы. Для проверки этой гипотезы в стационарном случае мы записывали модель в уровнях в виде:
уі, = ф1у? + tM-l+<оіУ\%+4jS+• • •+<л+лТР,у(>2-Р+аі+£і>
и проверяли гипотезу
#0: = Л2І = ... = Лрі = 0. Перепишем эту модель в виде:
yit = Pi Дуй + у* А/Д + Pi Ау\% + /І Ау(Л +...+
+pTp_h, AyZU + rU і *y*U+ «<•+іїу" + s?y\% + e» ■
При такой записи модели нулевая гипотеза принимает вид:
причем статистика F-критерия для проверки такой гипотезы численно идентична статистике F-критерия для проверки гипотезы Н0: Лиг = Л2І = ••• = &рі ~ 0-Но оценка для 8( имеет нестандартное распределение. Моделирование показывает, что при использовании F-критерия в подобных ситуациях слишком часто определяется ложная причинность по Грейнджеру.
Осложнений, возникающих при проверке гипотезы об отсутствии причинности по Грейнджеру в рамках уравнения для уровней, не возникает при проверке аналогичной гипотезы в рамках уравнения (6.3) для рядов разностей, т.е. для VAR в разностях.
Коинтегрированная VAR
Если имеем дело с коинтегрированной VAR, компоненты которой являются /(І)-рядами, модель (6.2) можно записать в форме модели коррекции ошибок (error correction model — ЕСМ):
ДУ, = & АУг+ • • • + Ср+ а + BATyt_x + et,
где 5 — (Nx г)-матрица коэффициентов адаптации;
А — (N х г)-матрица, столбцы которой представляют г линейно независимых коинтегрирующих векторов; г — ранг коинтеграции, 1 < г < N 1 (при г = О коинтеграции нет; при г = N все ряды стационарны).
Если At — /-я строка матрицы АТ9 то линейные комбинации zx = Axyt_X9 zr Aryt_, стационарны, и потенциально все эти стационарные линейные (коинтегрирующие линейные) комбинации должны быть включены в правые части уравнений системы в качестве объясняющих переменных:
+ (СІГ1) АД +... + С&~1)*Ук ) +
Дум = (CnАд ,-i + • • • + & А?* ) + (а2/ Дд ,_2 +... + C£NAyNt ,_2) +... + + Ад +... + йРм] АУм ) +
+ Я* + 5iVlZl, /-1 + • • • + BNrZr, /-1 +£Nf
При этом обязательно должно выполняться условие В ф О, так что хотя бы один из коэффициентов BiJ9 і = 1, N9 j = 1, г, должен быть отличен от нуля. Если это, скажем, коэффициент BiJ9 то в прогнозировании /-й переменной помогают, во всяком случае, прошлые значения тех переменных, у которых коэффициенты в у-й коинтегрирующей линейной комбинации отличны от нуля.
Если компоненты ряда>>, являются /(І)-рядами и ранг коинтеграции равен 1, то для оценивания модели коррекции ошибок можно использовать двухступенчатую процедуру Энгла — Грейнджера. В этом случае производят О/^-оценивание уравнения
Ум =М + Г2У2< +УъУъг ++ ^^/
получают оценки /і, у19 уЪ9 yN коэффициентов долговременного соотношения и на их основе — оценку
Ч = Уи-М-Г2У*-УъУъг-----ГмУм стационарной линейной комбинации
zu = Уи-М-ГіУь-ГзУ*— -ГмУп>
имеющей нулевое среднее.
Так построенную переменную zu подставляют вместо zu в правую часть уравнений системы в форме модели коррекции ошибок и производят OLS-оценивание коэффициентов последней. К оценкам всех коэффициентов этой системы, кроме коэффициента приг{ t_l9 применимы стандартные асимптотические выводы, поскольку это коэффициенты при стационарных переменных. Вследствие наличия коинтеграции оценки а, уъ уъ, yN суперсостоятельны, и это приводит к тому, что получаемая в итоге оценка для коэффициента при zXt_x имеет ту же асимптотику, что и оценка коэффициента при стационарной переменной zXt_x в уравнении ЕСМ с известной zlr Таким образом, при наличии единственной (с точностью до нормировки) коинтегрирую-щей линейной комбинации компонент вектора yt стандартные асимптотические результаты остаются в силе для всех коэффициентов ЕСМ, оцениваемой на втором шаге процедуры.
J Замечание 6.1.3. Стандартные (асимптотические) процедуры проверки гипотез о параметрах ЕСМ могут применяться к любым гипотезам, не включающим предположения Вхх = ... = Вт 0, соответствующего некоинтегрированности компонент ряда уг При гипотезе Н0: Вхх = ... = BNX = 0 асимптотическое распределение оценок коэффициентов ВХХ9 Вт нестандартное и зависит от мешающих параметров.
Рассмотренная в разд. 11 ч. 2 данного учебника процедура Йохансена использует метод максимального правдоподобия и позволяет:
оценивать ранг коинтеграции;
проверять гипотезы о ранге коинтеграции;
оценивать коинтегрирующие векторы, соответствующие выбранному рангу коинтеграции;
проверять гипотезы о выполнении тех или иных ограничений на коэффициенты коинтегрирующих векторов.
В отличие от процедуры Энгла — Грейнджера, здесь ранг коинтеграции может быть любым. Однако недостатками этой процедуры являются большая чувствительность к отклонениям распределения случайных ошибок от нормального и то, что для получения удовлетворительных результатов она требует большого количества наблюдений (около 100 и даже более).
Для коинтегрированной двумерной VAR ранг коинтеграции равен г = 1, так что ЕСМ имеет вид:
+ (С1(Г,)Ад.-р+.+^"1)д>'2,,-р+.) + + al+Buzu_i+elt,
Ау2, = (^Дд,., + &)&Уг,-1) + (&)&Уи-г +^22)Aj2>,-2) + + + (^Г>и_р+1+^Г1)А>'2>,-,+1) +
ИЛИ
+ <Г1(11)Лд,_1 +Л2)ДУи-2 +--+ ЛР"1)АДг-р+1 +
+ Сп*У2, t-x + ^12 }АУ2, / -2 + •' • + ІЇҐ^Уі, ,-^1 + *1,> АУ2/ = ^2+521ZU-l +
+ £1)ЛДм + £?)ЛД,-2 + + ЙГ1)АУі,г.р+і +
+ ^22 4У2./-1 +^222)^2,,_2 + .-. + ^'1)АУ2,/-#,+1 + *2,>
где
Поскольку хотя бы один из коэффициентов Вхх или В21 должен быть отличен от нуля (иначе не было бы коинтеграции), это означает, что в правую часть хотя бы одного из двух уравнений ЕСМ входит в качестве объясняющей переменная zXt_x = >'1жГ_1 /и УіУі^-х И, следовательно, в таком уравнении имеет место причинность по Грейнджеру. Например, если в уравнении для Ауи отличен от нуля коэффициент Ви, то значениег-1 помогает в прогнозировании значения yXt наряду со значением yXt_, и запаздывающими разностями Ауи_19 Ау1в,_2, ДУі,/-р+іПоскольку причинность по Грейнджеру в коинтегрированной двумерной VAR существует по крайней мере в одном направлении, фактически вопрос может стоять только о том, существует ли G-причинность в выбранном направлении — например, в направлении от ряда>>2, к ряду уХг В последнем случае гипотеза об отсутствии такой причинности сводится к гипотезе:
н0-.ви=о, c$ = cl?=... = Clrl)=o>
которую можно проверить стандартными методами, даже если использовать вместо значений zXt_x значения zXt_x = yXft-i ft УгУї^-х с fi> їі-> полученными на первом шаге процедуры Энгла — Грейнджера.
Методология Тода — Ямамото
Выше было показано, как можно проводить проверку на причинность по Грейнджеру, когда:
VAR стационарна;
VAR состоит из /(І)-рядов и они не коинтегрированы (следует перейти к VAR в разностях);
VAR состоит из Д1)-рядов, и они коинтегрированы.
Применение соответствующих методов требует предварительной проверки гипотезы единичного корня для определения порядков интегрированное™ рядов и проверки гипотезы об их коинтегрированности/некоин-тегрированности. Однако критерии для проведения такой проверки обычно обладают малой мощностью, и это ограничивает применение указанных методов.
Тода и Ямамото {Toda, Yamamoto, 1995) предложили процедуру, позволяющую обойти эти проверки.
Тода и Ямамото исходят из модели DGP:
Уг =Го+Гі^... + Г/+П^м+... + П^+^,
где st ~ lid., E(st) = О, Cov(st) = X, Esit2+6 < оо для некоторого 8> 0.
Для проверки гипотезы об отсутствии причинного влияния тех или иных переменных на другие переменные предлагается проверять эту гипотезу в рамках расширенной статистической модели:
где
p>k + d, d — порядок интегрированное™ ряда yt.
В качестве d обычно берется dmax — предполагаемый максимальный порядок интегрированное™ рядов в составе уг
Гипотезы отсутствия причинности по Грейнджеру в DGP затрагивают
в такой постановке только элементы матриц Ии (и не затрагивают
остальных матриц в SM, т.е. матриц Т1к+и П^). Если гипотеза накладывает т линейных ограничений на элементы этих матриц, то статистика Вальда для проверки этой гипотезы имеет асимптотическое распределение хт)-При этом ряд yt может быть стационарным, 1(1) или 1(2), причем в каждом случае — еще и относительно линейного тренда, и если это 1(1)или 7(2)-ряд, то он может быть и коинтегрированным.
Рассмотрим статистическую процедуру выбора количества запаздываний. Запишем DGP в виде: yt=n+nt + -.> + Yqtq +Uxyt_x+... + nkyt_k+... + npyt_p+et9
где
П*+1=... = Пр=0, p>k + d. (6.4)
Оценим аналогичную SM, но без ограничения (выражение (6.4)), и проверим гипотезу
#0*:П/+1=... = П„=0, где *</</?-1,
т.е. гипотезу о невхождении в DGP лагов более высокого порядка, чем /. Если эта гипотеза верна, то статистика Вальда для проверки этой гипотезы имеет асимптотическое распределение хп2(Р ~ ОХ если l^d.
Заметим, что если k > d9 то / > к > d. Следовательно, если порядки интегрированное™ рядов не превышают истинного количества запаздываний в DGP, то применима обычная процедура выбора количества лагов в VAR.
В частности, если d = 1, то процедура выбора порядка модели всегда асимптотически обоснованна. Если же d = 2, то она асимптотически обоснованна только при к > 1.
При выборе порядка модели можно использовать также информационные критерии.
Резюмируем сказанное: при подозрениях на возможную интегрирован-ность или коинтегрированность рядов в составе yt гипотезу Н0 можно проверять, не производя собственно проверки рядов на интегрированность и коинтегрированность, а лишь позаботившись о том, чтобы SM в виде VAR имела порядок (к + dmax).
Используя стандартную асимптотическую теорию, можно проверять и другие линейные (и многие нелинейные) ограничения на первые к матриц коэффициентов.
J Замечание 6.1.4
Добавление лишних лагов может значительно понизить мощность критериев, если количество рядов N велико.
В модель можно также включать сезонные дамми-переменные.
J Замечание 6.1.5. Говоря о причинности по Грейнджеру в моделях нестационарных VAR, следует, вообще говоря, различать причинность в долгосрочном плане (long-run) и причинность в краткосрочном плане (short-run).
Если рассматривается некоинтегрированная УАК(р) с /(^-переменными, то, переходя к модели в разностях, получаем VAR со стационарными переменными. Для простоты пусть VAR связывает две переменные (N= 2), так что VAR в разностях имеет вид:
АУіг = «і + tfJWi +Л2)Л*г-2 ++ ^і(Г1)АУи-р+і +
+ tf" ДУ2, /-1 + ^12 }AV2, г-2 + • • • + Сії'"ДУ2, + *1, >
Ду2, = ог2 + ^1)Дд,_1 +^i}AyU-2 + + ^2Г1}ДД/.Р+і +
+ ^}АУ2.М +^222)ДУ2,.-2 ++ ^22"1)АУ2,/-Р+1 + *2г
Если в первом уравнении = =... = Cn~l) = О» то не яв" ляется G-причиной для ух в краткосрочном плане. Если во втором
уравнении \%2 =£г -= £г~1) = ®> то У не является G-причиной для у2 в краткосрочном плане. При этом асимптотически оправданно использование F-критериев для проверки линейных гипотез о коэффициентах этой VAR, так что проверка выполнения этих соотношений может осуществляться на основе соответствующих F-критериев.
Если рассматривается коинтегрированная VAR(p) для двух /(І)-переменньгх, то в рамках соответствующей модели коррекции ошибок:
AyXt = ax+BxxzXtt_x +
+ ^ДДм + ^2)Дд,-2 + ... + ^(Г1)Ауи.р+і + + С$?*У2. t-i + #22)4у2. t-i +... + СІГ1) AV2., -/m-l + ^lf>
+ ^11)Дд,_1 + <Г<2)Дд,_2 +... + ^\%Wi +
+ ^4^2,/-! +^222)ДДг-2 +.-. + ^22"1)AV2,r-P+l +*2r>
можно проверять как гипотезы об отсутствии краткосрочной G-при-чинности одной из переменных в отношении другой (выражаемые
соотношениями Сп = Сії = • • • = Сп~1) = 0 и = = ... = 0 = О соответственно), так и гипотезы об отсутствии долгосрочной G-при-чинности одной из переменных в отношении другой (выражаемые соотношениями Вхх = 0иВ2Х = О соответственно). При этом гипотеза об отсутствии G-причинности в выбранном направлении — например, в направлении от^2 к^ — формулируется следующим образом:
Н0:Вп=0, CV=£$=... = tiV)=0Именно в таком виде гипотеза об отсутствии G-причинности в направлении от у2 к ух рассматривалась ранее, при обсуждении коинтегрированных VAR.
ПРИМЕР 6.1.1
Обратимся к рассмотренной в работе (beeper, Sims, Zha, 1996) модели, в которой были использованы переменные:
LP =
Обсуждение Эконометрика Книга вторая Часть 4
Комментарии, рецензии и отзывы
