3.5. интервальная оценка функции регрессии и ее параметров

3.5. интервальная оценка функции регрессии и ее параметров

Доверительный интервал для функции регрессии. Построим доверительный интервал для функции регрессии, т.е. для условного математического ожидания М^У), который с заданной надежностью (доверительной вероятностью) у = 1—а накрывает неизвестное значение MX(Y).

Найдем дисперсию групповой средней j>, представляющей

выборочную оценку MX(Y). С этой целью уравнение регрессии (3.12) представим в виде:

у = у + Ь{(х-х). (3.28)

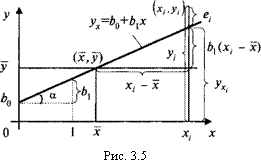
На рис. 3.5 линия регрессии (3.28) изображена графически. Для произвольного наблюдаемого значения уі выделены его

составляющие: средняя у, приращение -Зс), образующие расчетное значение у(, и остаток е,.

Дисперсия групповой средней равна сумме дисперсий двух независимых1 слагаемых выражения (3.28):

GJ^vj+Glix-xy. (3.29)

(Здесь учтено, что (jc-jc) — неслучайная величина, при

вынесении которой за знак дисперсии ее необходимо возвести в квадрат.)

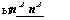о2у=о2

= —. (3.30)

Для нахождения дисперсии представим коэффициент регрессии (3.16) в виде

1 п

i=i

1=1

lL(xi-x)2

/=і

(3.31)

1 Доказательство этого факта здесь не приводится.

65

Тогда

£(x,-x)V

r2 _J=L

(3.32)

Найдем оценку дисперсии групповых средних (3.29), учитывая (3.30) и (3.32) и заменяя а2 ее оценкой s2:

1 (х-х)2 • +

(3.33)

П 1(х,-1)2

/=1

Основываясь на предпосылках 1—5 регрессионного анализа

у — М (Y)

(§ 3.4), можно показать, что статистика t-- —— имеет

/-распределение Стьюдента с k = п — 2 степенями свободы и построить доверительный интервал для условного математического ожидания Мх (Y):

У-*-а;к 'Sy<Mx(Y)<y + tx_a,k -Sy,

(3.34)

где sy =^sj — стандартная ошибка групповой средней у.

Из формул (3.33) и (3.34)

0

видно, что величина (длина) доверительного интервала зависит от значения объясняющей переменной х. при х — х она минимальна, а по мере удаления х от х величина доверительного интервала увеличивается (рис. 3.6). Таким образом, прогноз значений (определение неизвестных значений) зависимой переменной Y по уравнению регрессии оправдан, если значение х объясняющей переменной X не выходит за диапазон ее значений по выборке (причем тем более точный, чем ближе X к Зс). Другими словами, экстраполяция кривой регрессии, т.е. ее использование вне пределов обследованного диапазона значений объясняющей переменной (даже если она оправдана для рассматриваемой переменной исходя из смысла решаемой задачи) может привести к значительным погрешностям.

Доверительный интервал для индивидуальных значений зависимой переменной. Построенная доверительная область для M^Y) (см. рис. 3.6) определяет местоположение модельной линии регрессии (т.е. условного математического ожидания), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней. Поэтому при определении доверительного интервала для индивидуальных значений уо зависимой переменной необходимо учитывать еще один источник вариации — рассеяние вокруг линии регрессии, т.е. в оценку суммарной дисперсии sj следует

включить величину s2. В результате оценка дисперсии индивидуальных значений уо при х = Xq равна

Уо

1 , 1 , Ро"*)2

(3.35)

V

1-1 J

а соответствующий доверительный интервал для прогнозов индивидуальных значений yl будет определяться по формуле:

УО -h-a;n-2Sy0 < У0 ^ У0 + 'l-a;*-2^j>0 • (3.36)

Доверительный интервал для параметров регрессионной модели.

Наряду с интервальным оцениванием функции регрессии иногда представляет интерес построение доверительных интервалов для параметров регрессионной модели, в частности для параметров регрессионной модели, в частности для Pi и а2.

Можно показать, что при выполнении предпосылки 5 (с. 61)

регрессионного анализа статистика t

имеет стандарт-

ный нормальный закон распределения, а если в выражении (3.31) для Pi заменить а2 ее оценкой s2, то статистика

(3.37)

t =

' ~2

^1 "Pi

I i=i

имеет /-распределение Стьюдента с к = п — 2 степенями свободы. Поэтому (см. § 2.7) интервальная оценка параметра (Зі на уровне значимости а имеет вид:

Ь ~ t-a;n-2 l ^ Pi ^ Ьх + tx_a.n_2 . =• (3.38)

При построении доверительного интервала для параметра

ns2

а2 исходят из того, что статистика имеет \%2 -распределение с

а2

k = п — 2 степенями свободы. Поэтому интервальная оценка для а2 на уровне значимости а имеет вид (см. (2.43)):

ns2 Л . ns2

2 <о2<— (3.39)

Ха/2;л-2 Хі-а/2;л-2

(доверительный интервал выбирается таким образом, чтобы

Р(У} <Х?-а/2;*-2)=^Х2 >г1,2-п-і) = у)► Пример 3.3.

По данным табл. 3.1: 1) оценить сменную среднюю добычу угля на одного рабочего для шахт с мощностью пласта 8 м;

найти 95\%-ные доверительные интервалы для индивидуального и среднего значений сменной добычи угля на 1 рабочего для таких же шахт;

найти с надежностью 0,95 интервальные оценки коэффициента регрессии pi и дисперсии а2.

Решение. Уравнение регрессии Y по X было получено в примере 3.1: у = -2,75 +1,016х , т.е. при увеличении мощности

пласта Хш I м добыча угля на одного рабочего Y увеличивается в среднем на 1,016 т (в усл. ед.).

1. Оценим условное математическое ожидание M^iY). Выборочной оценкой Mx=s(Y) является групповая средняя ух=&, которую найдем по уравнению регрессии:

^=-2,75+1,016-8=5,38 (т).

Для построения доверительного интервала для My=\%(Y) необходимо знать дисперсию его оценки, т.е. sj g. Составим

вспомогательную таблицу (табл. 3.2) с учетом того, что Зс =9,4 (м), а значения определяются по полученному уравнению регрессии.

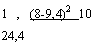= 0,189

и ^ =ДЇ89 = 0,435 (т).

По табл. II приложений ґо,95;8=2,31Теперь по (3.34) искомый доверительный интервал

5,38-2,31 • 0,435 < M^Y) < 5,38+2,31 • 0,435,

или 4,38 < Л/*=8( У) < 6,38 (т).

Итак, средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 4,38 до 6,38 т.

2. Чтобы построить доверительный интервал для индивидуального значения j*o=8, найдем дисперсию его оценки по (3.35):

si = 1,049

ґи 1 ( (8-9,4)^ 10 24,4

= 1,238

и syvt =VU38=1,113 (т).

Далее искомый доверительный интервал получим по (3.36):

5,38-2,31 • 1,113<^*о=8< 5,38+2,31 • 1,113,

или 2,81<^о=8< 7,95.

Таким образом, индивидуальная сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 2,81 до 7,95 т.

3. Найдем 95\%-ный доверительный интервал для параметра Pi.

По формуле (3.38)

,,0,6-2,3l45!<P, <Ш6 + 2,3,Щ,

или 0,537 < Pi < 1,495 , т. е. с надежностью 0,95 при изменении

мощности пласта Іна 1 м суточная выработка Y будет изменяться на величину, заключенную в интервале от 0,537 до 1,495 (т).

Найдем 95\%-ный доверительный интервал для параметра а2.

Учитывая, что а= 1—0,95=0,05, найдем по таблице III приложений

Ха/2;я-2 = \%0,025;8 = 17,53 5С?-а/2;л-2 = \%0,975;8 =2,18.

По формуле (3.39)

10 1,049 9 10-1,049

<<jz<

17,53 2,18

или 0,598 < а2 < 4,81, и 0,773 < а < 2,19.

Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,598 до 4,81, а их стандартное отклонение — от 0,773 до 2,19 (т). ►