5. система одновременных эконометрических уравнений

5. система одновременных эконометрических уравнений

Систему взаимосвязанных тождеств и регрессионных уравнений, в которой переменные могут одновременно выступать как результирующие в одних уравнениях и как объясняющие в других, принято называть системой одновременных (эконометрических) уравнений. При этом в соотношения могут входить переменные, относящиеся не только к моменту времени t , но и к предшествующим моментам. Такие переменные называются лаговыми (запаздывающими). Тождества относятся к функциональной связи переменных и вытекают из содержательного смысла этих переменных. Техника оценивания параметров системы эконометрических уравнений имеет свои особенности. Это связано с тем, что в регрессионных уравнениях системы независимые переменные и случайные погрешности оказываются коррелированы между собой. Достаточно хорошо изучены статистические свойства и вопросы оценивания систем линейных уравнений. Будем рассматривать линейную модель вида

Р;1 y1t + Р; 2 У It + ... + + Yn X1t + ... + Y*x*t = Ut , (5.1)

где t=1,2,...,n; i=1,2,...,g;

Yt значение эндогенной (результирующей) переменной в момент времени t; xjt значение предопределенной переменной, т. е. экзогенной (объясняющей) переменной в момент t или лаговой эндогенной переменной;

uit случайные возмущения, имеющие нулевые средние.

Совокупность равенств (4.9) называется системой одновременных уравнений в структурной форме. Наличие априорных ограничений, связанных, например, с тем, что часть коэффициентов считаются равными нулю, обеспечивает возможность статистического оценивания оставшихся. В матричном виде систему уравнений можно представить как Byt + rxt = є t , (5.2)

где В-матрица порядка g х g, состоящая из коэффициентов при текущих значениях эндогенных переменных;

Г-матрица порядка g х k, состоящая из коэффициентов экзогенных переменных.

yt = (yltygt)T ; Xt = (X1txKt)T ; єt = (suєg)T векторы-столбцы значений соответственно эндогенных и экзогенных переменных, случайных ошибок. При этом Mst = 0; Z(E) = МєtєT = a2t En, где En единичная матрица. Таким образом, если

Ме єt = 0 при t1 Ф t2 и t1, t2 = 1,2,...,n, то случайные ошибки независимы между собой.

Если дисперсия ошибки постоянна Мє2 = о2 = о2 и не зависит от t и xt, то это свидетельствует о гомоскедастичности остатков. Условием гетероскедастичности является зависимость значений Мє J2 = о2 от t и xt. Умножив все элементы уравнения слева на обратную матрицу Sj, получим приведенную форму системы одновременных уравнений:

yt = B-Txt + B-4 . (5.3)

Среди систем одновременных уравнений наиболее простыми являются рекурсивные системы, для оценивания коэффициентов которых можно использовать метод наименьших квадратов. Систему (5.3) одновременных уравнений называют рекурсивной, если выполняются следующие условия:

1) Матрица значений эндогенных переменных

В=

( 1

/21

0

1

0 ■■■ 0^ 0 ■ •• 0

0

g 2

1

является нижней треугольной матрицей, т. е. Д _ 0 при j>i и /;i _ 1;

случайные ошибки независимы между собой, т. е. aii > 0, аij _ 0 при j , где i,j=1,2,...,g. Отсюда следует, что ковариационная матрица ошибок M(stsTt ) _Z(Є) диаго-нальна;

каждое ограничение на структурные коэффициенты относится к отдельному уравнению. Процедура оценивания коэффициентов рекурсивной системы с помощью метода наименьших квадратов, примененного к отдельному уравнению, приводит к состоятельным оценкам. В качестве примера рассмотрим ситуацию, которая приводит к рекурсивной системе уравнений. Предположим, что цены на рынке Pt в день t зависят от объема продаж в предыдущий день qt-1, а объем покупок qt в день t зависит от цены товара в день t. Математически систему уравнений можно представить в виде

Pt _ а0 + a1qt-1 + £ t,

Случайные возмущения £t и §t можно считать независимыми. Мы получили рекурсивную систему двух уравнений, причем в правую часть первого уравнения входит предопределенная переменная qt-1, а второго эндогенная переменная Pt.

Применение метода наименьших квадратов для получения оценок системы одновременных уравнений приводит к смещенным и несостоятельным оценкам, поэтому область его применения ограничена рекурсивными системами. Для оценивания систем одновременных уравнений в настоящее время наиболее часто используют двухшаговый метод наименьших квадратов, применяемый к каждому уравнению системы в отдельности, и трехшаговый метод наименьших квадратов, предназначенный для оценивания всей системы в целом. Двухшаговый метод наименьших квадратов (2 МНК) применяют для оценки отдельного уравнения системы одновременных уравнений. Сущность этого метода состоит в том, что для оценивания параметров структурного уравнения метод наименьших квадратов применяют в два этапа. Он дает состоятельные, но в общем случае смещенные оценки коэффициентов уравнения, является достаточно простым с теоретической точки зрения и удобным для вычисления. Запишем исходное i-е структурное уравнение системы в виде

У, _ + X уг + £ i где yt вектор п наблюдений над i-й эндогенной переменной; Y матрица порядка (п хqг.) значений эндогенн^1х переменных, входящих в i-е уравнение (кроме yt -й);

Pt вектор размерности (qt х 1) значений структурных коэффициентов эндогенных переменных из матрицы Y;

X г матрица порядка (n х к г) значений экзогенных переменных, входящих в уравнение;

вектор размерности (кг х 1) коэффициентов, относящихся к переменным Xt; єг вектор случайных возмущений, имеющий размерность (n х 1), причем Мєг = 0;

2(є) = о 2 Е n.

Непосредственно применить в данном случае метод наименьших квадратов нельзя, так как эндогенные переменные, содержащиеся в матрице Y коррелированы со случайными составляющими єг.

В связи с этим представим эндогенные переменные Y, входящие в уравнение, как функцию всех содержащихся в модели экзогенных переменных (X). Найдем оценку матрицы Y, которая согласно методу наименьших квадратов определяется из выражения

Y = хг (xTxt )-1 xty .

Тогда

= Y + U, где U матрица оценок остаточных величин преобразованной системы. Исходное структурное уравнение может быть преобразовано к виду:

Уг = Щ + Xt y + v, ,

где

+ Up

Применяя метод наименьших квадратов для нахождения оценок параметров вновь полученного уравнения регрессии, будем иметь:

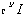d

г J

f P г ^

V Yг

f YTYt;

XT1Yl;

t ^ ^ 1 f fT

XTXi j

J

где d вектор оценок коэффициентов размерности ((q; + кг) х 1). Перейдя к исходным переменным, получим:

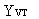d

J

f Р г ^

V Yг

(

YTX1 (XTX1)1 XTYf;

X TY ;

Y X

YTX (XTX)1 XTy;

Полученная оценка и носит название оценки двухшагового метода наименьших квадратов параметров p и y .

Таким образом, двухшаговый метод наименьших квадратов состоит в замене матрицы Y расчетной матрицей Y, после чего оцениваются коэффициенты обыкновенного

уравнения регрессии yг на Y и X t. Согласно алгоритму трехшагового метода наименьших квадратов первоначально с целью оценки коэффициентов каждого структурного уравнения применяют двухшаговый метод наименьших квадратов, а затем определяют оценку для ковариационной матрицы случайных возмущений. После этого с целью оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. Рассмотрим систему одновременных уравнений, содержащую g эндогенных и к экзогенных переменных, принимаемых как неслучайные. Преобразуем i-е уравнение (5.3) к виду:

где

Zt (Y1X1 ) , б, =

Умножив левую и правую части уравнения слева на транспонированную матрицу XT значений всех экзогенных переменных модели, получим

XTyt XTZt бі + XTєi. Записав таким образом все уравнения системы, получим

Xі у XTyt

0

X Z,

0 XTZ 2

о Y бЛ Г xt є, ї

+

0

б

v хЧ J

0

0

XTZ

XT є

gJ

Для применения обобщенного метода наименьших квадратов построим ковариационную матрицу вектора возмущений

(

on XT X

ал XT X

o XT X

o 2 gXTX

Z ® XTX *

vogiXTX L o,XTX

ogX Xj

Заменив матрицу Z (oц) ее оценкой S (siJ), получим оценку ковариационной матрицы вектора возмущений

S (хТх)

и соответствующую обратную матрицу

S"1) S-1 ® (хТх)-1. Тогда искомая оценка трехшагового метода наименьших квадратов имеет вид:

б (ATS(U) A)-1ATSU)Z

Прямое (кронекерово) произведение матрицы А={а^}, i=1, 2,..., n и J=1, 2,...,m и матрицы В размерности (kxl) обозначается А <8> В и представляет собой матрицу размерности (nkxml) вида:

a

A ® B

aimB

anlB

anjB "• anmB J

Каждый элемент этой матрицы представляет собой матрицу a^B размерности kxl.

где

A

X Z1 0

0

0

XTZ 2

0

0 0

XTyg J

В случае, когда матрица Z не является диагональной, т. е. когда возмущения, входящие в различные структурные уравнения, зависимы, трехшаговая процедура имеет лучшую асимптотическую эффективность по сравнению с двухшаговой.