8.4.2 рыночный риск портфеля
8.4.2 рыночный риск портфеля
В общем случае можно заметить, что чем более диверсифицирован портфель (т.е. чем большее количество ценных бумаг в него входит), тем меньше каждая доля X.. При этом значение $р1 не меняется существенным образом, за исключением случаев преднамеренного включения в портфель ценных бумаг с относительно низким или высоким значением «беты». Так как «бета» портфеля является средним значением «беты» ценных бумаг, входящих в портфель, то нет оснований предполагать, что увеличение диверсификации портфеля вызовет изменение «беты» портфеля и, таким образом, рыночного риска портфеля в какую-либо сторону. Таким образом, можно утверждать, что:
диверсификация приводит к усреднению рыночного риска.
Этот вывод имеет важное значение, так как в случае плохого или хорошего экономического прогноза большинство ценных бумаг упадут или соответственно возрастут в цене. Несмотря на уровень диверсификации портфеля, всегда можно ожидать, что такие рыночные явления будут влиять на доходность портфеля.
8.4.3 Собственный риск портфеля
Совершенно другая ситуация возникает при рассмотрении собственного риска портфеля. В портфеле некоторые ценные бумаги могут возрасти в цене в результате распространения неожиданных хороших новостей, касающихся компаний, эмитировавших данные ценные бумаги (например, о приобретении патента). Другие ценные бумаги упадут в цене в результате распространения неожиданных плохих новостей, относящихся к данным компаниям (например, об аварии). В будущем можно ожидать, что количество компаний, о которых станут известны какие-либо хорошие новости, приблизительно будет равняться количеству компаний, о которых станут известны какие-либо плохие новости, что приведет к небольшому ожидаемому чистому воздействию на доходность хорошо диверсифицированного портфеля. Это означает, что чем больше диверсифицируется портфель, тем меньше становится собственный риск и, следовательно, общий риск.
Данная величина может быть точно вычислена, если ввести предположение о некоррелированности случайных отклонений доходностей, что и было сделано при написании уравнения (8.11в). Рассмотрим следующую ситуацию. Если предположить, что во все ценные бумаги инвестировано одинаковое количество средств, то доля X составит /N, а уровень собственного риска, как это показано в уравнении (8.11 в), будет равен:
1
(8.12а)
2 1 или а = —
г" N
2 і 2 , _i_ 2 El е2 eW
N
(8.126)
Значение, находящееся внутри квадратных скобок в уравнении (8.126), является средним собственным риском ценных бумаг, образующих портфель. Но собственный риск порфеля в N раз меньше данного значения, так как член /N находится вне квадратных скобок. Далее, если портфель становится более диверсифицированным, то количество бумаг в нем (равное N) становится больше. Это также означает, что величина 1/Nуменьшается, что приводит к уменьшению собственного риска портфеля12. Можно сделать следующее заключение:
диверсификация существенно уменьшает собственный риск.
Проще говоря, портфель, состоящий из 30 или более случайно выбранных ценных бумаг, будет иметь относительно низкую величину собственного риска. Это означает, что общий риск будет ненамного больше величины имеющегося рыночного риска. Таким образом, указанные портфели являются хорошо диверсифицированными. Рисунок 8.12 показывает, как диверсификация приводит к снижению собственного риска и усреднению рыночного риска.
8.4.4 Пример
Рассмотрим две ценные бумаги А и В, о которых шла речь ранее. Эти бумаги имеют коэффициенты «бета», равные 1,2 и 0,8 соответственно; стандартные отклонения их случайных погрешностей составляют 6,06 и 4,76\%. Таким образом, из заданных значений аы = 6,06\% и асВ = 4,76\% следует, что о= 6,Об2 = 37 и atB= 4,762 = 23. Теперь предположим, что стандартное отклонение рыночного индекса о7 составляет 8\%. Это подразумевает, что дисперсия рыночного индекса равняется 82, или 64. Используя уравнение (8.8), получим значения дисперсии для ценных бумаг Aw В:
<^ = (1,22х64) + 37= 129; <4 = (0,82х 64) + 23 = 64.
 рРа;
рРа;
N
Портфель, состоящий из двух ценных бумаг
Рассмотрим комбинацию ценных бумаг А и В в портфеле, образованном вложением равного количества денег инвестора в каждую ценную бумагу. То есть рассмотрим портфель, в котором ХЛ = 0,5 и Хв = 0,5. Так как Р^ = 1,2 и Ря/ = 0,8, то «бета» данного портфеля может быть вычислена с помощью уравнения (8.10в):
= (0,5 х 1,2) + (0,5 х 0,8) = 1,0.
Используя уравнение (8.11в), можно вычислить дисперсию случайного отклонения портфеля о:
ор = (0,52 х 37) + (0,52 х 23) = 15. Из уравнения (8.11а) видно, что портфель будет иметь следующую дисперсию:
с2р = (1,02 х 64) + 15 = 79.
Данное выражение представляет общий риск портфеля, состоящего из двух ценных бумаг.
Портфель, состоящий из трех ценных бумаг
Рассмотрим, что произойдет при комбинировании первых двух ценных бумаг с третьей ценной бумагой (С) в случае формирования портфеля, состоящего из трех ценных бумаг, взятых в равной пропорции (ХА = Хв = Хс = 0,33). Третья бумага имеет «бету», равную 1,0, и случайную погрешность, стандартное отклонение которой (оЕс) составляет 5,50\%. Таким образом, дисперсия случайной погрешности оЕС равняется 5,52, или 30, а дисперсия ценной бумаги вычисляется по формуле:
о2с = (1,02 х 64) + 30 = 94.
Прежде всего отметим, что портфель, состоящий из трех ценных бумаг, имеет такой же уровень рыночного риска, как и портфель, состоящий из двух ценных бумаг, так как оба портфеля имеют «бета»-коэффициент, равный 1,0:
Р^ = (0,33 х 1,2) + (0,33 х 0,8) + (0,33 х 1,0) = 1,0.
Таким образом, увеличение диверсификации не привело к изменению уровня рыночного риска. Вместо этого оно привело к усреднению рыночного риска.
При использовании уравнения (8.11 в) дисперсия случайного отклонения портфеля может быть вычислена следующим образом:
ар = (0,332 х 37) + (0,332 х 23) + (0,332 х 30) = 10.
Отметим, что дисперсия случайного отклонения портфеля, состоящего из трех ценных бумаг, меньше дисперсии портфеля, состоящего из двух ценных бумаг (т.е. 10 < 15). Таким образом, в данном примере увеличение диверсификации действительно уменьшило собственный риск.
Из уравнения (8.11а) можно заметить, что портфель, состоящий из трех ценных бумаг, имеет следующую дисперсию:
о2р = (1,02 х 64) + 10 = 74.
Это выражение представляет общий риск портфеля, значение которого меньше, чем значение общего риска портфеля, состоящего из двух ценных бумаг (74 < 79). Таким образом, увеличение диверсификации привело к снижению общего риска.
■j^^H Краткие выводы
Эффективное множество содержит те портфели, которые одновременно обеспечивают и максимальную ожидаемую доходность при фиксированном уровне риска, и минимальный риск при заданном уровне ожидаемой доходности.
Предполагается, что инвестор выбирает оптимальный портфель из портфелей, составляющих эффективное множество.
Оптимальный портфель инвестора идентифицируется с точкой касания кривых безразличия инвестора с эффективным множеством.
Предположение о вогнутости эффективного множества следует из определения стандартного отклонения портфеля и из существования финансовых активов, доходности которых не являются совершенно положительно или совершенно отрицательно коррелированными.
Диверсификация обычно приводит к уменьшению риска, так как стандартное отклонение портфеля в общем случае будет меньше, чем средневзвешенные стандартные отклонения ценных бумаг, входящих в портфель.
Соотношение доходности ценной бумаги и доходности на индекс рынка известно как рыночная модель.
Доходность на индекс рынка не отражает доходности ценной бумаги полностью. Не-объясненные элементы включаются в случайную погрешность рыночной модели.
Уровень наклона в рыночной модели измеряет чувствительность доходности ценной бумаги к доходности на индекс рынка. Коэффициент наклона носит название «бета»-коэффициент ценной бумаги.
В соответствии с рыночной моделью общий риск ценной бумаги состоит из рыночного риска и собственного риска.
Вертикальное смещение, «бета»-коэффициент и случайная погрешность портфеля являются средневзвешенными значениями смещений, «бета»-коэффициентов и случайных погрешностей ценных бумаг, входящих в портфель, причем вес каждой бумаги равен ее доле в общей стоимости портфеля.
Диверсификация приводит к усреднению рыночного риска.
Диверсификация может значительно снизить собственный риск.
Вопросы и задачи
Почему можно предположить, что отдельно взятые ценные бумаги лежат в правой части множества достижимости, в то время как в левой верхней части этого множества находятся только портфели?
Объясните, почему большинство инвесторов предпочитают иметь диверсифицированные портфели, вместо того чтобы вкладывать все свои средства в один финансовый актив. Для объяснения своего ответа используйте изображения множества достижимости и эффективного множества.
Почему можно ожидать, что большинство обыкновенных акций, выпускаемых в США, имеют положительную ковариацию? Приведите пример двух обыкновенных акций, которые, как вы ожидаете, будут обладать очень высокой положительной ковариаци-ей. Приведите пример двух обыкновенных акций, которые, как вы ожидаете, будут обладать очень низкой положительной (или даже отрицательной) ковариацией.
Объясните, почему понятия ковариации и диверсификации тесно связаны между собой.
Мул Хаас является управляющим портфелем. В среднем все ценные бумаги, которые рассматривает Мул, имеют положительную ожидаемую доходность. При каких условиях Мул может захотеть приобрести ценную бумагу с отрицательной ожидаемой доходностью?
В терминах модели Марковица объясните на словах и с помощью графиков, как инвестор выбирает свой оптимальный портфель. В какой особой информации нуждается инвестор для определения данного портфеля?
Дод Бринкер обладает портфелем, состоящим из двух ценных бумаг, взятых в следующих долях и имеющих следующие ожидаемые доходности и стандартные отклонения:
Ценная бумага
Ожидаемая доходность
Стандартное отклонение
Доля
А В
10\% 15 20\% 25 0,35 0,65
Для различных уровней корреляции этих ценных бумаг определите максимальное и минимальное значения стандартного отклонения портфеля.
Кратко объясните, почему эффективное множество должно быть вогнутым.
Лесли Нунмакер обладает портфелем, рыночная модель которого записывается следующим образом:
г = 1,5\% + 0,90г, + є ,.
р ' ' ' pi
Какой будет ожидаемая доходность портфеля Лесли, если ожидаемая доходность на индекс рынка составляет 12\%?
Каким образом выводится «бета»-коэффициент из рыночной модели ценной бумаги? Почему ценные бумаги с «бета»-коэффициентом больше 1 называются «агрессивными»? Почему ценные бумаги с «бета»-коэффициентом меньше 1 называются «оборонительными»?
В следующей таблице приведена информация о доходностях акций Glenwood City Properties и индекс рынка за десять лет. Постройте кривую доходности Glenwood City, на которой по вертикальной оси откладывается доходность на акции Glenwood City, а по горизонтальной — доходность на индекс рынка. По данным точкам нарисуйте ваше представление о рыночной модели. Пользуясь данным графиком, получите оценку «бета»-коэффициента акции Glenwood City.
| Год | Glenwood City | Индекс рынка |
| 1 | 8,1\% | 8,0\% |
| 2 | 3,0 | 0,0 |
| 3 | 5,3 | 14,9 |
| 4 | 1,0 | 5,0 |
| 5 | -3,1 | -4,1 |
| 6 | 3,0 | -8,9 |
| 7 | 5,0 | 10,1 |
| 8 | 3,2 | 5,0 |
| 9 | 1,2 | 1,5 |
| 10 | 1,3 | 2,4 |
Рассмотрите акции двух компаний — Woodwill Wisel Farms и New Richmond Furriers.
а. Если вам известно, что коэффициент наклона в рыночной модели для Woodwill
составляет 1,20, а для New Richmond — 1,00, акции какой компании являются
более рискованными в контексте портфеля? Почему?
 |
погрешности для акций Woodwill составляет 10,0\%, а для New Richmond — 21,5\%,
изменится ли ваш ответ? Объясните.
Рыночная модель определяет очень простое взаимодействие доходности ценной бумаги и доходности на индекс рынка. Объясните некоторые сложности реального мира, которые могут уменьшить «пророческую силу» рыночной модели.
Имеются два портфеля, один инвестирован в компанию по энергоснабжению, другой — в компанию по добыче золота. Каждый портфель имеет коэффициент «бета», равный 0,60. Почему для аналитика рынка ценных бумаг интересно знать, что портфель, инвестированный в золотодобычу, имеет большее стандартное отклонение случайной погрешности (собственный риск), чем портфель, инвестированный в энергоснабжение?
Акции Lindon Station имеют «бета»-коэффициенты, равные 1,20. В течение пяти лет следующие доходности были получены на акции Lindon и на индекс рынка.
Предполагая, что коэффициент смещения рыночной модели равен 0\%, вычислите стандартное отклонение случайной погрешности рыночной модели за данный период.
Почему диверсификация приводит к уменьшению собственного риска, но не рыночного риска? Приведите и интуитивное, и математическое объяснение.
Сиги Боски имеет портфель, составленный из трех ценных бумаг со следующими характеристиками:
Ценная бумага «Бета»-коэффициент Стандартное отклонение Доля
случайной погрешности
А 1,20 5\% 0,30
В 1,05 8 0,50
С 0,90 2 0,20
Каким будет общий риск портфеля Сиги, если стандартное отклонение индекса рынка равняется 18\%?
Рассмотрим два портфеля: один, состоящий из четырех ценных бумаг, а второй -из десяти. Все ценные бумаги имеют «бета»-коэффициент, равный единице, и собственный риск в 30\%. В обоих портфелях доли всех ценных бумаг одинаковы. Вычислите общий риск обоих портфелей, если стандартное отклонение индекса рынка составляет 20\%.
(Вопрос к приложению.) Что такое «угловой» портфель? Почему «угловые» портфели важны для определения вида эффективного множества?
(Вопрос к приложению.) Почему подход с использованием рыночной модели технически проще, чем оригинальный подход Марковица к конструированию эффективного множества?
(Вопрос к приложению.) Если дисперсия индекса рынка равна 490, а ковариация ценных бумаг А и В равняется 470, чему равняется «бета» ценной бумаги В, если известно, что «бета» ценной бумаги А равняется 1,20?
(Вопрос к приложению.) Как много параметров нужно оценить, чтобы провести анализ характеристик по риску и доходности портфеля, состоящего из 50 ценных бумаг, используя: (а) оригинальный подход Марковица; (б) подход, использующий рыночную модель?
Приложение А
Модель Марковица
Определение структуры и местоположения эффективного множества
Ранее было отмечено, что существует бесконечное число портфелей, доступных для инвестора, но в то же время инвестор должен рассматривать только те портфели, которые принадлежат эффективному множеству. Однако эффективное множество Марковица представляет собой изогнутую линию, что предполагает наличие бесконечного числа точек на ней. Это означает, что существует бесконечное количество эффективных портфелей! Как может быть использован подход Марковица, если инвестору необходимо определить структуру каждого из бесконечного числа эффективных портфелей? К счастью, нет поводов для отчаяния. Марковиц видел эти потенциальные проблемы и внес основной вклад в их преодоление, представив метод их решения13. Он включает в себя алгоритм квадратического программирования, известный как метод критических линий (critical-line method).
Хотя данный алгоритм и выходит за рамки данной книги, необходимо понимать, как он работает. Для начала инвестор должен оценить вектор ожидаемых доходностей и ковариационную матрицу. Например, рассмотрим портфель из трех акций, представленный ранее в данной главе14. Проведем оценку вектора ожидаемых доходностей, обозначенного как ER, и ковариационной матрицы, обозначенной как VC:
| 16,2 " | 146 | 187 | 145 | ||
| ER = | 24,6 | VC= | 187 | 854 | 104 |
| 22,8 | 145 | 104 | 289 |
Затем через алгоритм определяется количество «угловых» портфелей, которые связаны с ценными бумагами и полностью описывают эффективное множество. «Угловой» портфель — это эффективный портфель, обладающий следующими свойствами: любая комбинация двух смежных «угловых» портфелей представляет из себя третий портфель, лежащий в эффективном множестве между двумя «угловыми» портфелями. Данное утверждение можно проиллюстрировать примером.
Алгоритм начинается с определения портфеля с наивысшей ожидаемой доходностью. Данный портфель соотносится с точкой S на рис. 8.1 и является эффективным портфелем. Он состоит только из одной ценной бумаги с наибольшей ожидаемой доходностью. То есть если инвестор хочет приобрести данный портфель, все, что он должен сделать, это купить акции компании с наивысшей ожидаемой доходностью. Любой другой портфель будет иметь меньшую ожидаемую доходность, так как в конечном счете часть фондов инвестора будет помещена в акции других компаний, имеющих ожидаемую доходность ниже S.
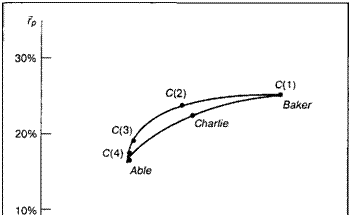
Например, компанией, акции которой наиболее доходны, является компания Baker. Соответствующим эффективным портфелем будет первый «угловой» портфель, определенный алгоритмом. Его состав описывается следующим вектором весов, обозначенным Х(1):
Х(1) =
0,00 1,00 0,00
Его ожидаемая доходность и стандартное отклонение связаны только с ожидаемой доходностью и стандартным отклонением акций Baker и соответственно составляют 24,6\% и (854)1/2, или 29,22\%. На рис. 8.13 данный «угловой» портфель обозначен как С(1).
Затем алгоритм определяет второй «угловой» портфель. Данный портфель располагается на эффективном множестве ниже первого «углового» портфеля. Его состав определяется следующим вектором весов, обозначенным Х(2):
Х(2)-
0,00 0,22 0,78
То есть второй «угловой» портфель представляет собой портфель, в котором инвестор вкладывает 22\% своих фондов в обыкновенные акции компании Baker, а 78\% в обыкновенные акции компании Charlie. Подставляя данные веса в уравнения (7.3а) и (7.7), можно вычислить ожидаемую доходность и стандартное отклонение данного «углового» портфеля, которые составляют соответственно 23,20 и 15,90\%. На рис. 8.13 данный «угловой» портфель обозначен как С(2).
Говоря о первом и втором «угловых» портфелях, важно отметить, что они являются смежными эффективными (adjacent) портфелями и любой эффективный портфель, лежащий в эффективном множестве между двумя данными, будет представлять собой просто комбинацию их составов. Например, эффективный портфель, лежащий посередине между ними, будет иметь следующий состав:
| 0,00 | 0,00 | 0,00' | |||
| [0,5 х*(!)] +[0,5 хЛГ(2)] = 0,5 х | 1,00 | + 0,5х | 0,22 | = | 0,61 |
| 0,00 | 0,78 | 0,39 |
 10\%
10\%
20\%
30\% ар
Рис. 8.13. «Угловые» портфели
Таким образом, веса распределены следующим образом: 0,61 в акции Baker и 0,39 — в акции Charlie. Используя уравнения (7.3а) и (7.7), можно вычислить ожидаемую доходность и стандартное отклонение данного портфеля, которые составляют 23,9 и 20,28\% соответственно.
Определив второй «угловой» портфель, алгоритм затем определяет третий. Он имеет следующий состав:
*(3) =
0,84 0,00 0,16
Эти веса теперь могут быть использованы для вычисления ожидаемой доходности и стандартного отклонения даного портфеля, которые равны соответственно 17,26 и 12,22\%. Как и два предыдущих, данный «угловой» портфель является эффективным и обозначается С(3) на рис. 8.13.
Поскольку второй и третий портфели являются смежными, то любая их комбинация является эффективным портфелем, лежащим в эффективном множестве между двумя данными. Например, если инвестор вкладывает 33\% своих фондов во второй «угловой» портфель, а 67\% в третий, то в результате получается эффективный портфель со следующим составом:
| 0,00 | 0,84 | 0,56" | |||
| [0,33 хХ(2)] + [0,67x^(3)] = 0,33 х | 0,22 | + 0,67 х | 0,00 | = | 0,07 |
| 0,78 | 0,16 | 0,36 |
Используя уравнения (7.3а) и (7.7), можно показать, что данный портфель имеет ожидаемую доходность 19,10\% и стандартное отклонение 12,88\%.
Ранее отмечалось, что только комбинация «угловых» смежных портфелей может дать эффективный портфель. Это означает, что портфели, представляющие собой комбинацию двух несмежных «угловых» портфелей, не будут принадлежать эффективному множеству. Например, первый и третий «угловые» портфели не являются смежными, следовательно, любой портфель, представляющий собой комбинацию двух данных, не будет являться эффективным. Например, если инвестор вложит 50\% своих фондов в первый «угловой» портфель, и 50\% — в третий, то результирующий портфель будет иметь следующий состав:
| 0,00 | 0,84 | 0,42' | |||
| [0,5 хХ([)] + [0,5хХ(3)] = 0,5х | 1,00 | + 0,5 х | 0,00 | = | 0,50 |
| 0,00 | 0,16 | 0,08 |
Можно показать, что при данных весах ожидаемая доходность и стандартное отклонение данного портфеля равны 20,93 и 18,38\% соответственно. Однако это неэффективный портфель. Так как его ожидаемая доходность (20,93\%) лежит между ожидаемой доходностью второго (23,20\%) и третьего (17,26\%) «угловых» портфелей, то с помощью комбинации этих двух смежных портфелей инвестор имеет возможность сформировать эффективный портфель, имеющий такую же ожидаемую доходность, но меньшее стандартное отклонение15.
Далее алгоритм определяет состав четвертого «углового» портфеля:
Х(4) =
0,99 0,00 0,01
Можно вычислить его ожидаемую доходность и стандартное отклонение, которые равны 16,27\% и 12,08\% соответственно. Определив данный портфель, соответствующий точке Ена. рис. 8.1 (и С(4) на рис. 8.13), имеющий наименьшее стандартное отклонение из всех достижимых портфелей, алгоритм останавливается. Четыре «угловых» портфеля, объединенных в табл. 8.1, полностью описывают эффективное множество, связанное с акциями Able, Baker и Charlie.
Изображение графика данного эффективного множества является простой задачей для компьютера, обладающего высокими графическими возможностями. Он может определить состав и соответственно ожидаемые доходности и стандартные отклонения каждого из 20 эффективных портфелей, равномерно распределенных между первым и вторым «угловыми» портфелями. Затем он последовательно соединит отрезками точки, соответствующие данным портфелям. Это придаст графику вид изогнутой линии, показанной на рис. 8.13, так как данные портфели расположены близко друг к другу.
Таблица 8.1
•Угловые» портфели в случае трех ценных бумаг
Веса «Угловые» портфели
«Угловые» Able Baker Charlie Ожидаемая Стандартное
портфели доходность отклонение
С(1) 0,00 1,00 0,00 24,60\% 29,22\%
С(2) 0,00 0,22 0,78 23,20 15,90
С(3) 0,84 0,00 0,16 17,26 12,22
С(4) 0,99 0,00 0,01 16,27 12,08
Продолжая в том же духе, можно построить 20 эффективных портфелей между вторым и третьим «угловыми» портфелями, а затем соответствующий сегмент эффективного множества. После того как данная процедура будет выполнена для следующего промежутка между третьим и четвертым «угловыми» портфелями, график будет полностью построен.
Qj^l Определение состава оптимального портфеля
После того как были определены структура и местоположение эффективного множества Марковица, можно определить состав оптимального портфеля инвестора. Портфель, обозначенный как О* на рис. 8.2, соответствует точке касания кривых безразличия инвестора с эффективным множеством. Процедура определения состава оптимального портфеля начинается с графического определения инвестором уровня его ожидаемой доходности. То есть из графика инвестор может определить, где располагается О*, а затем с помощью линейки отметить его ожидаемую доходность. Для этого следует провести из точки О линию, перпендикулярную вертикальной оси (с помощью компьютера это можно сделать значительно более точно).
Проведя данную операцию, инвестор теперь может определить два «угловых» портфеля с ожидаемыми доходностями, «окружающими» данный уровень. То есть инвестор может определить «угловой» портфель, который имеет ближайшую ожидаемую доходность, большую, чем у данного портфеля (ближайший «угловой» портфель, расположенный «выше» О), и «угловой» портфель с ближайшей, меньшей ожидаемой доходностью (ближайший «угловой» портфель, расположенный «ниже» О).
Если ожидаемая доходность оптимального портфеля обозначена как 7 * и ожидаемые доходности двух ближайших «угловых» портфелей обозначены как 7" и 7* соответственно, тогда состав оптимального портфеля может быть определен с помощью решения следующего уравнения относительно Y:
7* = (7-х Y) + [7»х (1 Y)]. (8.13)
Оптимальный портфель будет состоять из доли Y, инвестированной в ближайший «угловой» портфель, находящийся «выше» оптимального, и доли 1 — У, инвестированной в ближайший «угловой» портфель, расположенный «ниже» оптимального.
Например, если оптимальный портфель имеет ожидаемую доходность в 20\%, тогда можно заметить, что второй и третий «угловые» портфели являются верхним и нижним ближайшими «угловыми» портфелями, так как они имеют ожидаемую доходность в 23,20\% и стандартное отклонение в 17,26\%. Уравнение (8.13), таким образом, имеет следующий вид:
20\% = (23,20\% х Y) + [17,26\% х (1 Y)].
Решением данного уравнения является Y= 0,46. Это означает, что оптимальный портфель состоит на 46\% из второго «углового» портфеля и на 54\% из третьего «углового» портфеля. В терминах объема инвестиций в ценные бумаги компаний Able, Baker и Charlie данное утверждение принимает следующий вид:
| ' 0,00 | 0,84' | 0,45' | |||
| [0,46 х Х(2)] + [0,54 х Х(3)] = 0,46 х | 0,22 | + 0,54х | 0,00 | = | 0,10 |
| 0,78 | 0,16 | 0,45 |
Таким образом, инвестор должен вложить 45\% своих фондов в акции Able, 10\% — в акции Baker и 45\% — в акции Charlie.
В качестве обобщения можно сказать, что если векторы весов ближайших верхних и нижних «угловых» портфелей обозначены X* и X соответственно, то веса отдельных4цен-ных бумаг, составляющих оптимальный портфель, равняются (Yx X") + [(1 Y) х X ].
Приложение Б
Исходные данные, необходимые для определения местоположения эффективного множества
Для того чтобы определить эффективное множество, инвестор должен оценить ожидаемые доходности всех рассматриваемых ценных бумаг, а также их дисперсии и ковари-ации. Далее, можно определить оптимальный портфель, найдя точку касания кривых безразличия инвестора с эффективным множеством, как это показано на рис. 8.2.
Для определения эффективного множества нужно сделать следующие шаги. Первое, нужно оценить ожидаемую доходность каждой ценной бумаги. Если рассматривается N ценных бумаг, то нужно произвести оценку N параметров. Второе, нужно оценить дисперсию каждой из этих ценных бумаг. Для N рисковых ценных бумаг нужно провести оценку других N параметров. Третье, нужно оценить ковариацию каждой пары ценных бумаг. Для этого нужно оценить {N1 — N )/2 параметров16. Это означает, что общее число параметров, для которых необходимо провести оценку, равняется (N2 + ЗЛО/2:
Ожидаемые доходности N Дисперсии N
Ковариации (Л/2 Л/)/2
Всего (Л/2 3N)/2
Например, если мы рассматриваем 100 рисковых ценных бумаг, то нам необходимо произвести оценку 5150 параметров [(1002 + (3 х 100)/2], состоящих из 100 ожидаемых доходностей, 100 дисперсий и 4950 ковариации. Эти параметры могут быть оценены один за другим, что представляет задачу, требующую больших временных затрат и практически неразрешимую. К счастью, существуют альтернативы данному методу, одной из которых является метод, основанный на рыночной модели17.
При подходе, использующем рыночную модель, в первую очередь необходимо оценить ожидаемую доходность на рыночный индекс. Затем для каждой ценной бумаги нужно оценить коэффициент вертикального смещения и коэффициент «бета». В общей сложности надо произвести оценку (1 + 2N) параметров (1 для г,, 2УУдля коэффициента вертикального смещения и «бета»-коэффициентов для каждой из TV рискованных ценных бумаг). Полученные значения могут быть использованы для проведения оценок ожидаемой доходности каждой ценной бумаги с помощью уравнения (8.3), которое в данном случае имеет следующий вид:
(8.14)
Ранее ожидаемая доходность на индекс рынка была оценена в 5\%. Исходя из данной величины, ожидаемую доходность ценной бумаги А можно оценить в 8\%, так как коэффициент смещения и «бета»-коэффициент этой ценной бумаги были оценены в 2\% и 1,2 соответственно:
~гА = 2\% + (5\%х 1,2) = 8\%.
Аналогично, ожидаемая доходность ценной бумаги В может быть оценена в 3\%, так как оценка коэффициента смещения равняется —1\%, а «бета»-коэффициента — 0,8:
7д = -1\% + (5\%х0,8) = 3\%.
При использовании рыночной модели дисперсия ценной бумаги / может быть оценена как сумма произведения квадрата значения «бета»-коэффициента ценной бумаги на дисперсию индекса рынка и дисперсию случайной погрешности. Уравнение для данной операции приводилось ранее:
о>=№+о1Г (^)
где о,, обозначает дисперсию индекса рынка и a2ti обозначает дисперсию случайной погрешности для ценной бумаги /.
Предполагая, что дисперсия индекса рынка равняется 49, соответствующие дисперсии ценных бумаг А и В можно оценить следующим образом:
о^=(1,22х 49)+ 6,062 = 107,28; Од = (0,82 х 49) + 4,762 = 54,02.
Это означает, что оценка стандартных отклонений данных ценных бумаг равняется 10,36\% = V 107,28 и 7,35\% = ^54,02 соответственно.
В заключение отметим, что ковариация ценных бумаг / и j оценивается произведением трех чисел: «бета»-коэффициента /-й ценной бумаги, «бета»-коэффициентау'-й ценной бумаги и дисперсии индекса рынка. То есть можно использовать следующую формулу:
о-, = н,,Р>/" <8Л5> Таким образом, ковариация ценных бумаг А и В может быть оценена следующим образом:
аАіЯ= 1,2 x 0,8 x 49 = 47,04.
Итак, применяя подход, использующий рыночную модель для оценки ожидаемых доходностей, дисперсий и ковариации, следует определить следующие параметры:
Для индекса рынка:
Ожидаемая доходность (г,) 1
Дисперсия (о*) 1
Для каждой ценной бумаги:
Коэффициент вертикального смещения (а.,) N
«Бета» (Р„) N
Дисперсия случайной погрешности (о* ) N
Итого 3/V + 2
Таким образом, в рамках данного подхода для определения эффективного множества и оптимального портфеля необходимо произвести оценку 302 [(3 х 100) + 2] параметров для 100 рисковых ценных бумаг. После оценки этих 302 параметров не составляет труда применить уравнения (8.14), (8.8) и (8.15) для расчета ожидаемых доходностей, дисперсий и ковариаций рискованных ценных бумаг. Рассмотренный ранее метод альтернативной оценки всех параметров один за другим требует оценить 5150 параметров. Как можно заметить из данного примера, применение подхода, основанного на рыночной модели, значительно сокращает объем расчетов.
После того как были оценены ожидаемые доходности, дисперсии и ковариаций, необходимо ввести эти значения в компьютер. Затем компьютер может приступить к определению эффективного множества, используя «алгоритм квадратичного программирования»18. После этого оптимальный портфель инвестора может быть подобран с помощью определения точки касания кривых безразличия инвестора с эффективным множеством.
Примечания
1 Это следует из того факта, что на отрезке от 0 до 100 находится бесконечное множество чисел. Если предположить, что данные числа отражают долю вложений инвестора в акции Able, а 100 минус данные числа — в акции Baker, то мы имеем бесконечное множество портфелей, которые можно составить из этих двух ценных бумаг. При данном утверждеиии, однако, предполагается, что при желании инвестор может приобретать часть одной акции. Например, инвестор может купить не только одну акцию Able, но или 1,1, или 1,01, или 1,001 акции.
2 Для того чтобы определить состав портфелей из эффективного множества, инвестор должен решить задачу «квадратичного программирования». См. книгу Марковица Portfolio Selection (ссыл-ка'в конце главы), в частности с. 176—185.
3 Инвестор, нейтральный к риску, выберет портфель S, в то время как азартный инвестор выберет либо S, либо Я.
4 Данное «свойство кривизны» может быть также использовано для объяснения того, почему правая сторона множества достижимости имеет форму зонта, как это показано на рис. 8.2. Более подробное объяснение вогнутости содержится в Приложении А.
5 Это пример однофакторной модели, где фактором является доходность на индекс рынка (см. гл. 11 для получения дополнительной информации о факторных моделях; см. гл. 10, 23 и 26, в которых более подробно рассмотрены индексы рынка). В действительности модель имеет более общий характер, чем приведенная здесь, поэтому нет необходимости в использовании доходности именно на индекс рынка. Можно использовать доходность на любую переменную, такую, например, как предсказанный уровень увеличения промышленного производства или валовой внутренний продукт, если мы можем предположить, что она имеет большее влияние на доходность отдельных акций.
6 Будет технически более правильным обозначить стандартное отклонение случайной погрешности как о р так как оно измеряется относительно индекса рынка /. Обозначение / не приводится в данном случае для упрощения записи.
7 Так как диапазон относится к возможным результатам, а интервал — к вероятности возникновения различных результатов, то можно заметить, что колесо рулетки просто является удобной формой представления вероятностного распределения случайной погрешности. Обычно предполагается, что случайная погрешность имеет нормальное распределение.
8 Это возможно в том случае, если ценная бумага В имеет случайную погрешность, которой соответствует колесо рулетки с целыми значениями от —9\% до 9\%, но с интервалами между каждым целым числом от —5\% до 5\% в два раза большими, чем интервалы между целыми числами от -9\% до -6\% и от 6\% до 9\%. Это означает, что вероятность того, что случайная погрешность примет любое конкретное целое значение между —5\% и 5\%, равняется 2/з0, в то время как вероятность того, что случайная погрешность примет целое значение из интервала от —9\% до —6\% и от 6\% до 9\%, равняется '/зо' Методы оценки коэффициента «бета» приведены в гл. 17.
10 Если случайная погрешность принимает значение, равное нулю, то это означает, что ценная бумага лежит на линии. Однако вероятность такой ситуации мала для большинства ценных бумаг.
11 Приложение Б показывает, как можно использовать рыночную модель для оценки ожидаемых
доходностей, дисперсий и ковариации ценных бумаг из достижимого множества. Имея данные
оценки, можно последовательно определить эффективное множество. См. примечание 2.
12 В действительности все, что нужно для уменьшения собственного риска, — это постоянное сокращение максимального объема инвестиций в любую ценную бумагу при возрастании N.
13 Harry М. Markowitz, «The Optimization of the Quadratic Function Subject to Linear Constraints*,
Naval Research Logistic Quarterly, 3, nos. 1-2 (March-June 1956), pp. 111-133.
14 Данный пример основан на примере, приведенном Марковицем в книге «Portfolio Selection*
(New Haven, CT: Yale University Press, 1959), pp. 176-185.
15 В данном примере эффективный портфель, имеющий ожидаемую доходность в 20,93\%, может
быть определен с помощью решения следующего уравнения относительно Y: (23,20\% х Y) +
+ (17,26\% х (1 Y)) = 20,93\%. Так как это линейное уравнение с одним неизвестным, то его
легко решить. Решение Y= 0,62 показывает, что вложение 62\% инвестиций во второй «угловой»
портфель и 38\% (100\% — 62\%) в третий «угловой» портфель позволяет создать эффективный
портфель с такой же ожидаемой доходностью, но меньшим стандартным отклонением (равным
14,09\%), чем портфель, состоящий наполовину из второго «углового» и наполовину из третьего
«углового».
"Данное число было получено следующим образом. Ковариационная матрица состоит из N строк и N столбцов, то есть из N1 ячеек, относящихся к параметрам, которые необходимо оценить. Диагональные ячейки содержат N дисперсий, учтенных ранее, следовательно, нам необходимо оценить (N2 N) ковариации. Так как ковариационная матрица является симметричной, то нам необходимо оценить только те ковариации, которые расположены ниже диагонали (поскольку симметричные элементы выше диагонали будут им равны), то есть нам остается оценить (N2 — N)/2 параметров.
17 Подход, использующий рыночную модель, является приблизительным подходом (как и все остальные альтернативные подходы), потому что он основан на ряде упрощений. Например, данный подход предполагает, что случайные погрешности любых двух ценных бумаг являются некоррелированными (предположение, необходимое для вывода уравнения (8.11с), а позднее уравнения (8.15)). Это означает, что результат поворота колеса рулетки для одной ценной бумаги
(такой, например, как Mobile) не оказывает никакого влияния на результат поворота колеса
рулетки для другой ценной бумаги (такой, например, как Exxon). Это предположение оспаривается в том случае, когда рассматриваются ценные бумаги, относящиеся к одной отрасли. См.:
Benjamin F. King, «Market and Industry Factors in Stock Price Behavior*, Journal of Business, 39, no. 1
(January 1966), pp. 139-170; and James L. Farrell, Jr., «Analyzing Covariation of Returns to Determine
Homogeneous Stock Groupings*, J
Обсуждение Инвестиции
Комментарии, рецензии и отзывы
