6.1.4. оценка опционов до момента окончания их срока

6.1.4. оценка опционов до момента окончания их срока

Обратимся к рассмотренному опциону на покупку с ценой реализации E = 100 руб. Если инвестор будет ждать окончания срока опциона или решит немедленно реализовать опцион (то есть потребовать от продавца опциона продать основную акцию), то стоимость опциона будет определяться соотношением рыночной цены акции Ps в момент реализации опциона и ценой реализации опциона E: если Ps > E, то стоимость опциона определяется разницей (Ps E); если Ps < E, то стоимость опциона равна нулю.

Стоимость опциона в момент его реализации является низшей из возможных цен опциона. Действительно, пусть Ps = 120 руб., и опцион на покупку стоит дешевле разницы (Ps E) = 120 -100 = 20 руб., например, 15 руб. Тогда владелец опциона, потратив на покупку опциона 15 руб., немедленно реализует его, то есть обяжет продавца опциона продать ему акцию по 100 руб., сразу же ликвидирует ее по рыночной цене 120 руб. и в итоге будет иметь прибыль, равную: 120 -100 -15 = 5 руб. (расчеты сделаны для одной акции). Такая ситуация называется «денежной машиной» и теоретически подобна вечному двигателю: инвестор «из воздуха» получил 5 руб. Если бы она была возможной, то все инвесторы сразу ей воспользовались, что немедленно вызвало бы рост стоимости опциона.

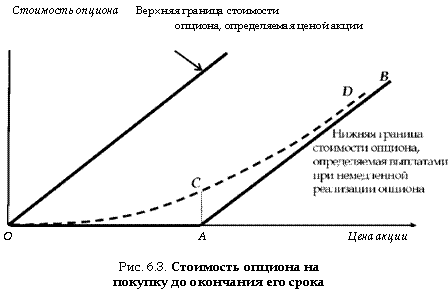
Если на рисунке 6.3 отразить стоимость опциона в случае его немедленной реализации, то линия OAB будет нижней границей возможной стоимости опциона на покупку.

Стоимость опциона на покупку до окончания его срока определяется кривой OCD (пунктирная линия). Она находится между

113 нижней (определяемой стоимостью опциона при его немедленной реализации) и верхней (определяемой стоимостью основной акции) границами.

4

С другой стороны, ни один опцион на покупку не может стоить больше цены основной акции, хотя бы потому, что выплаты владельцу опциона равны цене акции за вычетом цены реализации опциона. Значит, стоимость опциона должна описываться линией, лежащей между верхними и нижними границами возможной стоимости опциона. Теоретически стоимость опциона до момента истечения его срока обозначается пунктирной кривой OCD. Она начинается там, где пересекаются нижние и верхние границы стоимости опциона в начале координат, затем, по мере роста цены основной акции, повышается и в конечном итоге стремится к восходящему участку кривой нижней границы. Отсюда следует первый вывод о стоимости опциона: стоимость опциона повышается по мере роста цены основной акции (если, конечно, цена реализации опциона остается прежней).

Исследуем более внимательно очертания кривой OCD и ее местоположение. Для этого остановимся отдельно на точках O, C и D.

114

Точка О. Если стоимость акции ничтожна, то и опцион ничего не стоит. Стоимость опциона связана с будущей стоимостью акции. Если же акция ничего не стоит, то у нее нет и будущей стоимости. Зачем же покупать опцион на такую акцию?

Точка D. Когда цена основной акции становится выше, цена опциона приближается к цене основной акции за вычетом приведенной стоимости цены реализации опциона. Обратим внимание, что с ростом цены основной акции пунктирная линия становится практически параллельной восходящему участку нижней границы стоимости опциона. Это происходит потому, что с ростом цены акции возрастает вероятность того, что опцион обязательно будет реализован. Если стоимость акции достаточно высока, реализация опциона практически определена, поскольку вероятность падения цены основной акции ниже цены реализации становится слишком малой. Когда инвестор владеет опционом на покупку, который он однозначно намерен реализовать, то есть получить на него основную акцию (поскольку цена основной акции высокая), то можно считать, что он владеет этой акцией. Единственное различие состоит в том, что он не должен платить за нее полную цену вплоть до срока реализации опциона. В таком случае приобретение опциона на покупку акции эквивалентно покупке акции, часть которой оплачена как бы за счет занятых инвестором денег. Сумма якобы занятых денег равна приведенной стоимости цены реализации опциона.

Следовательно, стоимость опциона на покупку при высокой цене основной акции равняется цене акции за вычетом текущей стоимости цены реализации:

Voc = Ps PV(E).

Отсюда следует и другой вывод: если инвестор приобретает акцию путем предварительной покупки опциона, то он фактически получает кредит в рассрочку (инвестор платит цену опциона сегодня, но цена реализации выплачивается им в момент реализации опциона). Отсрочка платежа становится ощутимой, если безрисковая ставка процента достаточно высока и ожидаемый срок до реализации опциона велик. Таким образом, стоимость опциона возрастает с увеличением безрисковой ставки процента и срока до реализации опциона; в этом случае пунктирная кривая пойдет выше.

Точка С: в ней цена акции точно равна цене реализации опциона. Если бы опцион реализовывался немедленно, то его стои115 мость равнялась бы нулю. Однако, представим, что в этот момент до окончания срока опциона остается еще достаточно времени и у инвестора есть надежда, что цена акции за оставшийся период превысит цену реализации. Строго говоря, существует 0,5 вероятности того, что акция станет дороже и инвестор, в случае реализации опциона, получит выручку, равную разности между ценой акции и ценой реализации. Одновременно имеется 0,5 вероятности неудачного для инвестора исхода, когда цена акции понизится и он ничего не получит, так как не будет иметь смысл реализовывать опцион. Но если худший для инвестора вариант приносит нулевой результат, а равновероятный положительный результат дает определенную отдачу, то такой опцион обязательно должен иметь какую-то стоимость. Значит в точке С пунктирная кривая, соответствующая стоимости опциона до срока его окончания, обязательно должна проходить выше нижней границы, которая в точке С совпадает с осью абсцисс.

В общем случае цена опциона всегда выше нижней границы стоимости опциона, если еще есть время до окончания опциона. Чем выше разброс будущих значений цены основной акции относительно цены реализации, то есть чем выше стандартное отклонение случайных величин цены акции от цены реализации, тем больше ожидания инвесторов возможно более значительных величин цены акции, следовательно, тем выше располагается пунктирная кривая OCD на графике.

Приведенную стоимость любо средства (а значит и ее цену) можно найти, задав ожидаемые в будущем потоки денег от данной инвестиции и продисконтировав их за весь планируемый горизонт инвестиции. Почему же нельзя применить этот способ для оценки стоимости опциона? В принципе, первый этап прогнозирование будущих потоков денег от опциона вполне выполним. Невозможен второй шаг: риск, связанный с опционом, меняется каждый раз по мере изменения цены основной акции (чем выше цена, тем меньше риск). Кроме того, риск опциона меняется во времени, даже если цена акции не колеблется. Следовательно, невозможно задать однозначную ставку дисконта и продисконтировать будущие потоки денег.

Биномиальная модель. Решение проблемы оценки опционов пришло в 1973 году, когда американские экономисты Ф. Блэк и М. Шоулес открыли, что оценить стоимость опциона можно, если представить его отщонным эквивалентом так называемым репликант-ным портфелем, созданным путем покупки какого-то количества основных акций и займа определенной суммы по безрисковой ставке процента. Метод Блэка-Шоулеса применим только для европей116 ских опционов (срок реализации которых наступает в момент окончания опциона). Кроме того, имеется и еще одно ограничение: предполагается, что за время действия опциона по основной акции не выплачиваются дивиденды.

Простая биномиальная модель исходит из предположения, что в момент окончания опциона основная акция имеет одну из двух возможных цен. Предположим, что в настоящий момент (t = 0) цена акции компании «Орион» составляет 100 руб. и через год ее цена может либо возрасти до 125 руб., либо упасть до 80 руб. Допустим, что реальная безрисковая ставка процента rf = 7\% начисляется непрерывно в течение периода T, тогда за это время 1 руб. инвестиций возрастет до величины 1 х erT руб. Кроме того, срок опциона равен одному году и цена реализации опциона составляет 100 руб. Имеется также безрисковая облигация номиналом 100 руб. Необходимо создать репликантный портфель из акции и облигации, выплаты по которому в точности совпадут с будущими выплатами опциона. Тогда и стоимость такого портфеля будет равняться стоимости опциона.

Подойдем к решению задачи следующим образом: имеются три вида инвестиций: акция, облигация и опцион на покупку. Цена акции Ps = 100 руб. и ее возможные выплаты Psu = 125 руб. и Psd = 80 руб. известны. Также можно вычислить, что 100 руб., инвестируемые в безрисковую облигацию с непрерывно начисляемыми реальными 7\% годовых, дадут через год 107,25 руб. Наконец, известны и выплаты при реализации опциона: 25 руб., если цена акции через год составит 125 руб., и 0 руб., когда цена акции снизится до 80 руб. Неизвестна цена опциона. Сведем для наглядности исходные данные в таблицу 6.1.

Исходные данные для составления репликантного портфеля

Сформируем на основании этих данных репликантный портфель, выплаты по которому в точности соответствуют выплатам по

117 опциону на покупку в момент его реализации через год. Предположим, что этот портфель состоит из Ns акций и Nb облигаций. Если через год цена акции возрастет до 125 руб., то данный портфель обеспечит инвестору выплаты в размере: (Ns х 125 + Nb х 107,25). По условию, именно такие выплаты должен обеспечить при реализации через год опцион на покупку. Иными словами:

Ns х 125 + Nb х 107,25 = 25руб.

Если через год цена акции упадет до 80 руб., то выплаты по репликантному портфелю составят: Ns х 80 + Nb х 107,25, и эта величина должна равняться отдаче опциона при его реализации через год:

Ns х 80 + Nb х 107,25 = 0 руб.

Решая эти уравнения с двумя неизвестными, получим:

Ns = 25/45 = 0,5556 и Nb = -0,4144.

Что означают эти цифры с финансовой точки зрения? Реп-ликантный портфель создан следующим образом: инвестор приобретает 0,5556 акции компании «Орион» за свои деньги и коротко продает 0,4144 безрисковой облигации (инвестирование доли -0,4144 в облигацию стоимостью 100 руб. означает, что инвестор коротко продал безрисковую облигацию на сумму 41,44 руб. или, занял 41,44 руб. по безрисковой ставке 7\%). Подсчитаем отдачу нашего репликантного портфеля. Для случая роста цены акции до 125 руб. имеем:

125 х 0,5556 0,4144 х 107,25 = 69,45 44,45 = 25 руб.

Для случая снижения цены акции до 80 руб.:

80 х 0,5556 0,4144 х 107,25 = 44,45 44,45 = 0 руб.

Таким образом, путем комбинирования основной ценной бумаги и безрисковой облигации мы получили портфель, дающий инвестору точно такую же отдачу, как и опцион на покупку. Но тогда и стоимость такого портфеля должна равняться стоимости опциона. Стоимость портфеля равна: 55,5 6руб. (столько нужно денег, чтобы купить 0,5556 акции компании «Орион») минус 41,44 руб. (столько инвестор получил за счет короткой продажи безрисковой облигации, что он использовал на покупку акции). Итого стоимость оп118 циона на покупку равна: 55,56 41,44 = 14,12 руб. В общем случае, стоимость Vo опциона на покупку составляет:

Vo = NsxPs + NbxPb, (6.1)

где Pb и Ps цены безрисковой облигации и основной акции,

Ns и Nb количество акций и облигаций соответственно, которые необходимо объединить в репликантный портфель, чтобы он давал точно такие же выплаты, как и опцион на покупку в момент его реализации при истечении срока опциона.

Чтобы сформировать репликантн^гй портфель, инвестор должен занять определенную сумму денег и с ее помощью приобрести необходимое количество основных акций. Количество акций, необходимых, чтобы заменить один опцион на покупку, называется коэффициентом хеджирования, или опционной дельтой. В нашем случае коэффициент хеджирования h = 1/1,8 = 0,5556, то есть равняется величине Ns в формуле 6.1. Поскольку стоимость каждого опциона определяется h долями стоимости акции, то можно сказать, что каждый раз, когда стоимость основной акции изменяется на 1 рубль, стоимость опциона изменяется на h руб. Если обозначить Pou и Pod стоимости опциона при повышении цены акции (до Psu = 125 руб.) и при понижении цены акции (до Psd = 80 руб.) соответственно, то:

Pou Pod (25 0)

h = = = 0,5556.

Psu Psd (125 80)

То есть опционная дельта показывает реакцию цены опциона на возможные изменения цены акции в момент окончания опциона.

Проведенный анализ показывает, что при заданных:

а) цене реализации E = 100 руб.;

б) разбросе возможных верхних Psu = 125 руб. и нижних Psd = 80 руб.

цен основной акции через год;

в) безрисковой ставке процента rf = 7\%;

г) срока действия опциона T = 1 год;

д) исходной цене акции 100 руб.

цена опциона на покупку равняется 14,12 руб. Следовательно, задав эти пять характеристик, можно создать репликантный портфель на

119 основе композиции из основной акции и занятых сумм, имеющий такую же стоимость, что и опцион на покупку.

Чтобы создать эквивалент одному опциону на покупку необходимо приобрести h основных акций, где h коэффициент хеджирования, и занять определенную сумму В денег по безрисковой ставке. Эту сумму можно найти по формуле:

В = PV(h х Psd -Pod), (6.3)

то есть как приведенную стоимость выражения, заключенного в скобки. В рассматриваемом случае:

В = PV(0,5556 х 80 0) = (0,5556 х 80)Д,0725 = 41,44 руб.

Значит, в общем случае биномиальной модели стоимость Voc одного опциона на покупку может быть представлена в виде:

Voc = h^Ps В. (6.4)

Использование модели для опционов на продажу. Чтобы применить выводы биномиальной модели для оценки опционов на продажу, обратимся к основному равенству для европейских опционов и представим его в виде:

(стоимость опциона на продажу) = (стоимость опциона на покупку) -(стоимость основной акции) + (приведенная стоимость цены реализации),

или Vop = Voc Ps + PV(E). Стоимость опциона на покупку: Voс = h х х Ps В; приведенная стоимость цены реализации равна: E/erT, где T срок действия опциона. Следовательно:

E h х Psd + Pod

Vop = Psх(h 1) -B + E/erT = Psх(h 1) + .

Поскольку (h 1) < 0, то репликантный портфель для оценки опциона на продажу строится путем короткой продажи (1 h) акции и инвестирования в безрисковую облигацию суммы: (E h х Psd + + Pod)/erT. В нашем случае:

100 0,5556х80 + 0

Vop = -0,4444хPs + = 44,44 + 51,8 = 7,36 руб.

1,0725

120

Мультипериодный случай. Формула Блэка-Шоулеса. Мы выбрали период действия опциона в 1 год и исходили из того, что основная акция, стоившая 100 руб. в момент t = 0, через год может стоить либо 125 руб., либо 80 руб. Однако биномиальный метод можно применять, если предположить, что в течение годичного периода цена акции меняется не один раз (на практике именно это и происходит). В таком случае первоначальный период можно разбить на ряд интервалов и каждый последующий результат представить как следствие многочисленных биномиальных решений в предыдущие интервалы. Теоретически, если будут заданы все пять начальных характеристик, проведя расчеты от конца холдингового периода к началу, можно найти стоимость опциона в начальный момент t = 0. Специально запрограммированные калькуляторы позволяют проводить подобные вычисления.

Блэк и Шоулес вывели формулу оценки опциона для случая, когда длина интервала стремится к нулю. Если при этом предположить, что непрерывно начисляемая доходность акции распределена по нормальному закону, то цена опциона на покупку может быть вычислена по формуле:

Voc = O(di) xPs Ех(еіТ) хФ((І2), (6.5)

ln(Ps/E) + (if + ст2/2) хТ

di = , (6.6)

d2 = d1 — a Vt

где: Voc цена опциона на покупку;

Ps действующая (текущая) цена акции;

E цена реализации опциона;

rf безрисковая ставка процента*;

a стандартное отклонение норм отдачи акции;*

* Указанные величины зависят от длительности выбранного интервала. Можно взять любой интервал, но эти три величины должны браться за одинаковый промежуток времени: например, если выбран день, то надо брать дневную ставку процента и дневное стандартное отклонение.

121

T время действия опциона на покупку;*

Ф(сІ1) и Ф(сІ2) функции нормального распределения (определяются по таблицам).

Несмотря на «устрашающий» вид, формула 6.5 по сути является «раа1±иренным» вариантом формулы 6.4 и отражает уже известный факт:

стоимость опциона = [дельтахцена акции] [банковский заем], Ф((І1) х Ps Ф(сЬ) х PV(E).

Если цена акции станет значительной, то величины di и d2 возрастут, и функции Ф((1) и Ф((2) обе устремятся к единице. В этом случае цена опциона будет равняться цене акции за вычетом текущей стоимости цены реализации опциона:

Voс = Ps E/erT.

Этот вывод, мы уже получили, исследуя рисунок 8.3. Напомним, что формула 6.5 применима только для европейских опционов с учетом предположения, что за время действия опциона по основной акции не выплачиваются дивиденды.

Как следует из формулы 6.6, для нахождения цены опциона на покупку необходимо задать пять начальных параметров:

цену акции Ps

цену реализации опциона E

срок окончания опциона T

безрисковую ставку процента rf

стандартное отклонение а норм отдачи основной акции

Первые четыре параметра известны в исходный момент, а величину а надо находить. Причем формула 6.6 показывает, что стоимость опциона очень зависит от величины а. На практике используют два метода для оценки а: можно взять значения норм отдачи акции за прошедший период (от 30 до 90 дней профессионалы предпочитают оперировать дневными значениями rf и а, считая, что в этом случае формула Блэка-Шоулеса дает более точные результаты) и по ним выгаислить а ex post, то есть стандартное отклонение уже реализованных норм отдачи которое и нужно использовать в формуле 6.6. По второму методу, для нахождения а берется цена опциона в предыдущий день, подставляется в формулу 6.6, и уравнение решается относительно неизвестной а. К сожалению, прямое

122 решение этого уравнения невозможно, поэтому необходимо использовать специальные методы вычисления.

Формула Блэка-Шоулеса стала широко используемой и профессионалами, и тиндивтидуальными инвесторами. Она дает корректные оценки стоимости опционов. С определенными условиями ее можно применять и для оценки американских опционов, а также для европейских опционов, в случае выплаты по основной акции дивидендов за время действия опциона.