6.2. типовые примеры
6.2. типовые примеры
1. Меры риска ценных бумаг.
В данный момент акции Aw В имеют курсовые стоимости 50 и 20 руб., а их ожидаемые доходности тА = 12\%, аяд = 8\%. Инвестор имеет 100 тыс. руб. и хочет приобрести эти акции, вложив в каждый вид половину своего капитала. В конце года он собирается их продать и получить прибыль. Определить:
а) риск каждой акции и портфеля в целом, если ковариационная матрица доходностей (в виде десятичной дроби) будет равна:
'0,06250 0,00375 ,0,00375 0,02250
J
б) характеристику VAR, основанную на нормальном распределении и оценивающую максимально возможные потери капитала по уровню значимости 95\%.
Решение
а) риск акции определяется величиной СКО ее доходности:
ga = V0,0625 =0,25; ^ = ^/0,0225 =0,15.
Чтобы найти риск портфеля ар9 воспользуемся формулой дисперсии суммы:
Rp XARA + * А,
где R — доходность, х — доля вкладываемого капитала:
хА2аА2 + 2xjcBcov(RA, RB) + xb2gb2.
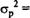
Согласно условию
ха = хв = °>5> а cov rb) = 0,00375, и, следовательно, ар2 = 0,52 • 0,0625 + 2 • 0,5 • 0,5 • 0,00375 + 0,52 • 0,0225 = 0,023125. Таким образом, риск доходности портфеля равен: ая=>/0,023125 «0,1521;
б) исходя из симметричности нормального распределения вероятностей, найдем интервал уклонения доходности портфеля от ее ожидаемого значения, задавшись уровнем значимости 0,9. Для рассматриваемого портфеля математическое ожидание его доходности составит:
/^=0,512 + 0,5-8= 10\%.
Согласно (6.8)
Bep(Rp 10\%| < б) = 2Ф(5/сд = 0,9.
Пользуясь таблицей значений функции Лапласа Ф(х), найдем:
8 = 1,64 • аР = 0,2494 = 24,94\%.
Тогда с вероятностью 0,9 данный портфель принесет доход в интервале от -14,94\% (10 24,94) до 34,94\% (10 + 24,94). Таким образом, при уровне значимости р = 0,9 + (1 — 0,9)/2 = 0,95 величина при риске по показателю доходности VAR^ 14,94\% (максимум потерь). Откуда следует, что по величине начального капитала VAR, = 14940 руб. Если считать относительно ожидаемой в конце года прибыли М (П) = 0,1 • 100 000 = 10 000 руб., то потери определят величину при риске относительно будущей стоимости портфеля VAR^7= 10000 + 14940 = 24940 руб. Ровно столько при наихудшем стечении обстоятельств потеряет инвестор относительно прогнозируемой им величины дохода при распродаже портфеля.
Дюрация как мера чувствительности.
В настоящий момент облигация продается за 1000 руб. при доходности 8\%. Ее дюрация составляет 10 лет. Насколько изменится цена этой облигации при увеличении доходности до 9\%?
Решение
Согласно определению, дюрация:
/>АР/Р ,
Аг/(1 + г)
где Р — текущая стоимость потока платежей; г — ставка дисконтирования.
По условию задачи:
/)= 10,/> = 1000,/-= 8\%, Аг= 1\%.
Отсюда получим следующее уравнение относительно неизвестной АР:
0= АР 1 + 0,08 ~1000" 0,01 '
и, следовательно, АР = 92,59 руб.
В результате измененная цена облигации приблизится к значению Ртм = 1000 92,59 * 907,4 руб.
Модель САРМ.
На идеальном финансовом рынке 10\% по стоимости составляют безрисковые бумаги и 90\% — рисковые. Рисковых всего три: первые составляют 1/6 их общей стоимости и их р = 0,8; вторые — 1/3 и р = 1. Каковы эффективности и р всех рисковых бумаг, средняя доходность тъ и коэффициент р2 по всему рынку, если средняя доходность по рисковым бумагам равна 8\%, а безрисковая ставка равна 4\%?
Решение
Эффективности первых двух бумаг получим, используя уравнение равновесного рынка (6.18):
т{ = 7,2\%; т2= 8\%.
Очевидно, что доля третьих бумаг равна половине стоимости всех рисковых активов (1 — 1/6 — 1/3).
Доходность рисковой части рынка равна взвешенной доходности ее компонент:
8\% = 1/6 • 7,2\% + 1/3 • 8\% + 1/2 • т3.
Отсюда получим эффективность третьей бумаги тъ = 124/15. Чтобы найти ее «бета», воспользуемся формулой (6.18):
т3 = 124/15 = 4 +Рз-(8-4),
и, следовательно, р3 = 16/15. Согласно условию задачи, 0,1 всего рынка составляют безрисковые бумаги, поэтому средняя доходность по всему рынку:
/?iz = 0,l 4 + 0,9-8 = 7,6\%.
Структура рисковой части рынка определяется долями хх = 1/6, х2 = 1/3, хъ = 1/2. Поэтому ее «бета»:
РРиск= 1/6-0,8 + 1/31 + 1/216/15=1,
что согласуется с теоретическим положением: коэффициент «бета» рыночного портфеля равен единице. Показатель «бета» для рынка в целом определим с учетом доли безрисковых бумаг:
Рі = 0,9-рриск=0,9.
4. Разложение риска на рыночный и индивидуальный. Среднеквадратическое отклонение (СКО) доходности рыночного портфеля составляет 20\%. Определить:
а) риск сильно диверсифицированного портфеля, если его
Р = 1,3;
б) риск сильно диверсифицированного портфеля с нулевым
значением Р;
в) р сильно диверсифицированного портфеля со стандартным
отклонением (СКО) в 15\%;
г) Р слабо диверсифицированного портфеля со стандартным
отклонением (риском), равным 20\%.
Решение
Для решения следует использовать соотношение (6.20), имея в виду, что у сильно диверсифицированного актива А индивидуальный риск оА * 0. Отсюда следует, что для рассматриваемых в первых трех вопросах портфелей их риск aL = р • ас = р • 20\%. Отсюда получим следующие ответы:
а) aL = 26\%;
б) aL = 0\%;
в) Р = (аї= 15\%)/20\% = 0,75;
г) у слабо диверсифицированного портфеля А индивидуальный
риск аА > 0, поэтому в разложении (6.20) присутствуют обе компоненты, и, следовательно, aL > Р • сгс. Подставив в это неравенство
исходные данные из п. «г», получим, что 20 > р • 20, т.е. р < 1.
5. Касательный портфель.
Запишите модель (6.15) для п = 2 и найдите касательный портфель при исходных данных:
/о= l\%,/wl = 2\%,5l = 1\%;т2 = 3\%,52 = 2\%;г12= 1/2.
Решение
Модель трехкомпонентного портфеля имеет вид с2 = G2x{2 + 2a1a2r12x1x2 + сг22дс22 -» min
х0 + jcj + х2 = 1
Согласно свойствам задачи (6.15), для любого портфеля на прямолинейном участке эффективной траектории отношение долей рисковых компонент будет таким же, как и у касательного портфеля С. Отсюда понятно, что для определения этого портфеля достаточно задаться такой правой частью т*9 для которой в оптимальном решении переменная х0опт > 0. Тогда доли вложения в касательном портфеле определятся в соответствии с правилом пропорционального деления в отношении
„ опт . опт
т.е.
_опт _опт
Г 1 Y 2
— * с2 —
Используя эти данные, найдем характеристики портфеля С: тс = тххсХ + т^с2, ос2 = o,Vс1 + 2o1a2r12x<.1xc2 + a2Vс2.
 = ВЗЛ2*В9Л2 + СЗЛ2*С9Л2 + 2*ВЗ*СЗ*В9*С9*А12;
= ВЗЛ2*В9Л2 + СЗЛ2*С9Л2 + 2*ВЗ*СЗ*В9*С9*А12;
в ячейки А16, А17 введем левые части ограничений:
= А6*АЗ + В6*ВЗ + С6*СЗ; = АЗ + В3 + С3,
а в ячейки D16, D17 — правые части ограничений, которые положим равными результату, вычисленному в ячейках А16, А17 после нажатия клавиши «Enter», т.е. числам 2 и 1.
Таким образом, процесс поиска решения начинается с допустимого плана х0 = 0,5; х1 = 0; х2 = 0,5 в сторону минимизации портфельного риска с и при неизменных требованиях относительно ожидаемой доходности тр = 2и единичного бюджета.
Для определения искомого портфеля С воспользуемся следующим соответствием между предназначенными для его характеристик ячейками и вводимыми в них формулами. Доли в касательном портфеле представлены в табл. 6.2.
Таблица 6.2
| хс2 | |
| В21 | С21 |
| =ВЗ/СУММ(ВЗ:СЗ) | =СЗ/СУММ(ВЗ:СЗ) |
Ожидаемая доходность и риск касательного портфеля даны в табл. 6.3.
 Чтобы перейти от допустимых значений переменных к их оптимальным значениям, выберем команду Сервис. Поиск решения и заполним открывшееся диалоговое окно «Поиск решения».
Чтобы перейти от допустимых значений переменных к их оптимальным значениям, выберем команду Сервис. Поиск решения и заполним открывшееся диалоговое окно «Поиск решения».
«Экранизация» ввода исходных данных и элементов формализации модели, а также диалогового окна «Поиск решения» на рабочем листе Excel имеет следующий вид (рис. 6.1).
После нажатия в открывшемся диалоговом окне на кнопку Выполнить появляется окно «Результаты поиска решения», которое сообщает, что решение найдено (рис. 6.2).
Таким образом, в оптимальном портфеле С на две стоимостные единицы ценных бумаг первого вида должна приходиться одна стоимостная единица бумаг второго вида (хс1« 0,6667; хс2« « 0,3333). Ожидаемая от этого портфеля доходность тс& 2,33\%, а его рискас« 1,15\%.
6. Линии рынков капитала и ценных бумаг.
Предположим, что ставка процента по безрисковым инвестициям равна 7\%, а ожидаемая доходность вложений в рыночный портфель составляет 10\% при риске 2\%.
Рассчитать ожидаемую доходность и риск портфеля, состоящего на 0,6 из рыночного портфеля и на 0,4 из безопасных инвестиций.
При заданных условиях составить уравнения линии рынка капитала и линии рынка ценных бумаг. Чему равны тангенсы углов наклона каждой из линий?
Пусть имеется инвестиционный проект (предполагаются инвестиции в ценные бумаги), ковариация доходности которого с рыночной равна 0,00064. Определить коэффициент р, ожидаемую требуемую рынком доходность этого проекта.
Если в настоящий момент ожидаемая доходность инвестиций равна 0,15, то, что, по вашему мнению, должно произойти?
Если в настоящий момент ожидаемая доходность инвестиций равна 0,1, а корреляция определяется условием 3, то как, по
переменны»
хО ХІ ї:Ж2
ояш одоош адзош ;
ДОХОДНОСТИ : j
1 поло ?дюо' здта
рИСКЙ і
оооос 'і даю 2ДШ
r12 'і
ОДГОі І е І І
функций ирм і
Поиск решения
ограничения
loodoi
1ДОЮ
пршыь части ограничений
2 даю
ЇДОЮ , ' л
Ж 21 Ж Ж
дош а касатальиш ггартфелз ?
касательный пзртф&ль
m IS ?
э,оо здг
Рис. 6.1. Исходные данные и диалоговое окно
А
jb_i,.- С
и
{переменные
:,у;{ o;*soo_,рдхю;_^cgssoq
;.4 j доходности «Sfo ml m2 ТГ* 1J000O 2ДЮ0? ЗДХЗО
ГУМ Vl s2 АЦ ' ОДЮО 'іДЮОГ Ч2ДХЮ
Ш
коэффициент к&рреляцим ода» :
{функция цели '
щ . :
IS І&грзничениа 1?! 1,0000
25|до/ш і яаеатольнам портье
21;} OJ6667 0,3233
ЖІ
Ш касательный портфель .25! 2,33 1.15
0.71500* ! Правые части ограничений 1ЯШ
Р*!5У ГС*>ТйТ&{ р*»Ш!г***$*
L
отчета
Pesyjtet-atta* Устф^нмвфсть
Рис. 6.2. Результаты поиска решения
вашему мнению, будет изменяться курсовая стоимость объекта вложений?
6. Чему равно значение р портфеля, в котором в равных долях присутствует безрисковый актив и вложения в инвестиционный проект(п.3)?
Решение
тр = 0,6 • 10 + 0,4 • 7 = 8,8\%, ар = 0,6 • 2 = 1,2\%.
В осях «доходность риск» линия рынка капитала определяется прямой, проходящей через две точки: одна из нцх соответствует безрисковому активу (г0 = 0,07; а — 0), другая рыночно2/w 7
му портфелю (тс = 0,1; ас = 0,02): а = —-у^-.
Тангенс угла наклона этой линии к оси От равен 2/3. В осях «коэффициент бета доходность» линия рынка ценных бумаг определяется прямой, проходящей через две точки: одна из них соответствует безрисковому активу (Р = 0; г0 = 0,07;), другая — рыночному портфелю (Рс=1; тс= 0,1): т = 0,03р + 0,07. Тангенс угла наклона этой линии к оси 0р равен 0,03.
Подставляя данные примера в формулу (6.18), найдем ожидаемую доходность инвестиционного проекта:
^проекта = 7\% + 0,00064/0,022 • (10\% 7\%) = 11,8\%.
Согласно условию, фактическое значение ожидаемой доходности отклоняется от теоретической оценки (6.18) на величину коэффициента а = 0,15 0,118 > 0. Положительность этого коэффициента свидетельствует о том, что объект инвестиций недооценен и следует ожидать повышения его курсовой стоимости.
В этом случае коэффициент а = 0,1-0,118<0и поэтому следует ожидать снижения курсовой стоимости.
р портфеля равно взвешенной сумме показателей коэффициентов р составляющих его активов: РП01УГфеЛЯ = 0,5 • 0 + 0,5 • 1,6 = 0,8.
Примечание. Выводы по п. 4 и 5 основаны на сравнении следующих текущих стоимостей:
ТСтсор=/У(1 +0,118), ТС4=/У(1 +0,15), ТС5 = = /У(1 + 0,1);ТС4<ТСтсор<ТС5.
Рыночная модель.
Дисперсия доходности по индексу рынка равна 490, а ко-вариация ценных бумаг А и В — 470. Чему равняется «бета» ценной бумаги В, если известно, что «бета» ценной бумаги А равняется 1,2? Решение
По свойству (6.22) рыночной модели
470
їл'Уі U-490
«0,8.
8. Платеж с поправкой на риск.
 Инвестор анализирует целесообразность приобретения сроком на один период акций А. Согласно прогнозам, в конце периода на рынке ценных бумаг возможны две ситуации, и на каждую из них акция А откликается неслучайным образом. Известны вероятности этих исходов и соответствующие им значения случайной эффективности рынка и случайного курса акции (табл. 6.4).
Инвестор анализирует целесообразность приобретения сроком на один период акций А. Согласно прогнозам, в конце периода на рынке ценных бумаг возможны две ситуации, и на каждую из них акция А откликается неслучайным образом. Известны вероятности этих исходов и соответствующие им значения случайной эффективности рынка и случайного курса акции (табл. 6.4).
Пусть доходность г0 безрисковых ценных бумаг составляет 8\%. Определить оценку теоретически справедливой текущей стоимости акции А методом корректировки ожидаемого платежа.
Решение
Используя табличные данные, найдем математическое ожидание и дисперсию рыночной доходности:
тс = 0,8 0,2 = 0,16;
с2 = M(RC)2 т2 = 0,8 • (0,2)2 (0,16)2 = 0,0064.
После этого вычислим параметр X, учитывающий поправку на риск в формуле безрискового эквивалента (6.24):
Х = (0,160,08)/0,0064 = 12,5.
Для определения этого эквивалента найдем ковариацию рыночной доходности Rc и случайного курса Е:
cov(£, R^ = М(Е M(E)){RC О, где М(Е) = 0,8 • 432 + 0,2 • 108 = 367,2, тс = 0,16.
Очевидно, что
М(Е M(E))(RC те) = М(Е • Rc) М(Е) • тс.
На основании этого:
cov(£, Rc) = (0,8 • 432 • 0,2 367,2 • 0,16) = 10,368.
Подставляя данное значение и величину X =12,5 в формулу (6.24), получим величину скорректированного платежа:
^скор.= 367>2 12>5 ' 10>368 = 367>2 129,6 = 237,6.
Дисконтируя ее по безрисковой ставке, придем к справедливой цене:
ТС = ^LL=220. 1,08
Если текущий курс акции меньше 220, то ее следует покупать, если же акция переоценена рынком, т.е. ее курсовая стоимость превышает найденную нами оценку, от покупки лучше воздержаться.
Примечание. Найденной оценке соответствует теоретически справедливая доходность акции RA = (E— ТС)/ТС, которая используется для расчетов скорректированной ставки (6.23):
гСкор= >о + X • cov((£220)/220, Rc) = 0,08 + 12,5 • cov(£, /у/220.
Согласно выполненным выше вычислениям, cov(£, Rc) = 10,368 и, следовательно, гскор = 0,08 + 12,5 • 10,368/220 » 0,6691. Дисконтируя ожидаемую величину платежа М(Е) по этой ставке (по рыночной цене капитального актива), получим тот же ответ, что и при решении задачи:
ТС = 367,2/1,6691 * 219,9988.
9. Процентная ставка с поправкой на риск.
Проект стоит 3 млн руб., рассчитан на 1 год с ожидаемой отдачей в размере 4,5 млн руб. и имеет «бету», равную 2,0. Рыночная премия за риск (гс г0) составляет 8\%, а текущая безрисковая ставка равна 7\%. Используя модель оценки долгосрочных активов (6.18), найти:
а) альтернативные издержки;
б) приведенную стоимость проекта.
Решение
а) по формуле (6.23) альтернативная ставка
г=7 + 2-8 = 23\%;
б) дисконтируя по скорректированной с учетом риска ставке
г = 23\%, получим приведенную стоимость проекта:
NPV= -3 + 4,5/1,23 * 0,658536 млн руб.
Обсуждение Задачи и тесты по финансовой математике
Комментарии, рецензии и отзывы
