Раздел 1 разовый платеж

Раздел 1 разовый платеж

1.1. Основные понятия и формулы

Правила приведения во времени. Согласно принципу временной неравноценности денег равновеликие, но разновременные денежные суммы оцениваются по-разному. Это свойство финансовых сопоставлений лежит в основе правил приведения денег во времени. В будущем денежные эквиваленты увеличиваются и отвечающие им суммы рассчитываются по формулам наращения. «Попятное» движение сопровождается снижением равноценных выплат, для определения которых используют формулы дисконтирования.

Общим правилам наращения и дисконтирования для произвольного срока предпошлем частный случай приведения на единичном периоде. В зависимости оттого, величина какого из концевых платежей считается базовой, т. е. принимается за 100\%, различают два варианта: 1) приведение по ставке начисления; 2) приведение соответственно ставке удержания процентов.

Вариант 1.

Пусть в качестве базовой рассматривается величина Р0 в начале периода. Тогда ставкой приведения г\% считается ставка начисления процента, т. е. тот процент, на который увеличится начальная сумма Р0 за один период. В результате наращенная за один период сумма Р{ составит величину:

рі=ро(1+т^г) = ^оО+0,

где ^ = Yqq — дробное измерение ставки.

Дисконтирование по этой ставке, называемой в этой связи еще и ставкой дисконтирования, заключается в приведении поздней выплаты Р{ к предшествующему эквиваленту Р0:

Вариант 2.

Пусть за базовую принята величина Р{ в конце периода. Тогда ставкой приведения q\% является ставка удержания процентов, ее еще называют учетной ставкой, т. е. тот процент, на который уменьшится финальная сумма Р на один период «назад». В этом случае процедура дисконтирования определяется формулой

р =РЛ—2-) = я (1-/),

а

где у = дробное измерение ставки.

100

Наращение по этой ставке, называемой еще ставкой наращения по учетному проценту, заключается в приведении ранней выплаты Р0 к последующему эквиваленту Р{

л .-а-.

1 (1-У)

По отношению к другим периодам («вперед» или «назад») формулы приведения определяются принятым правилом начисления (удержания) процентов: простых или сложных.

Согласно простым процентам приросты (удержания) денежных сумм на любом периоде составляют одну и ту же долю базовой величины. Отсюда получаются следующие формулы простых процентов:

Рп = Р0( + пі) наращение по простому проценту;

/>0 =—Ей— _ дисконтирование по простому проценту;

(1.1)

Рп =——— наращение по учетной ставке простого процента; (1-я/)

Р0 = Рп( — nj) — дисконтирование по учетной ставке простого процента.

Для сложных процентов одна и та же ставка берется не от базовой величины, а от результата предыдущего во времени приведения. В результате придем к формулам сложных процентов:

Рп = PQ(l + i)n наращение по сложному проценту;

(1 + /У

дисконтирование по сложному проценту;

Po

P„=(1.2)

(1-уУ

наращение по учетной ставке сложного процента;

Р0 = Рп( j)n дисконтирование по учетной ставке сложного процента.

Коэффициенты приведения денежных сумм в (1.1) и (1.2) называют множителем наращения Х(п і) и дисконтным множителем у(я; /), а промежуток приведения п измеряют в долях единичного периода, например года.

Приведение в «дробном» времени. Начисление процентов за дробное число лет может выполняться двумя методами:

по формуле сложных процентов:

S=P0(l + i)a + b;

смешанным методом:

S=P0(l + i)a( + Ы).

В этих формулах (а + Ь) — период приведения, а — целое число лет, b — дробная часть года.

Правила приведения в непрерывном времени. В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированный промежуток времени (год, полугодие, квартал и т.д.). В некоторых случаях для экономического анализа и в расчетах, связанных с непрерывными процессами, в математическом моделировании, а иногда и на практике — возникает необходимость в применении непрерывных процентов.

Правилу начисления по непрерывной ставке сложного процента отвечает такое изменение наращиваемой суммы S{t), при котором ее «привес» — процентные деньги за малый промежуток А/ — будет пропорционален длине этого промежутка и денежной сумме на его начало с коэффициентом пропорциональности 8:

S(t + At) S(t) = 8S(t)At.

Этому соотношению в непрерывном времени соответствует дифференциальное уравнение

§ = bS(t) at

с начальным условием S(0) = S0. Откуда получим следующие формулы наращения и дисконтирования:

5(0 = S0ebt9S0 = S(t)e-St. (1.3)

Процентная ставка 5 при непрерывном наращении имеет особое название — силы роста.

Согласно правилу простого процента непрерывно начисляемые проценты пропорциональны длительности времени начисления At и начальной сумме S(0) = 50, т.е.

S(t + At) S(t) = 8S(0)AL Предельным переходом при At -» 0, получим

^ = 55(0). at

Решая-это уравнение при условии S09 придем к формуле непрерывного наращения по простому проценту:

S(t) = S0(l + 8Г).

Эквивалентные процентные ставки. Эффективная ставка. Пусть разнородные процентные ставки (простая, сложная, учетная и т. д.) в конкретных условиях сделки приводят к одному и тому же финансовому результату. В этом случае они являются эквивалентными. Принцип эквивалентности ставок лежит в основе многих методов количественного финансового анализа. В частности, он позволяет перейти к единообразному показателю для сопоставимого оценивания эффективности финансовых операций.

В качестве такого показателя широко используют эффективную ставку, которая оценивает финансовую операцию годовой ставкой сложных процентов. Иначе говоря, эффективной ставкой ref называется годичная ставка сложных процентов, дающая то же соотношение между исходной суммой S0 и результирующей суммой ST, которая получена при любой схеме выплат. Формула эффективной ставки следует из этого определения:

S0(l+re/)T=ST.

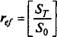
Откуда

\_

Т~1> (1.4)

где Т— время (в годах), за которое получен доход.

Согласно схеме /я-кратной капитализации на первоначальную сумму S0 в течение года начисляются проценты по годовой ставке /, причем число периодов начисления равно /и. Будучи продолжено на Глет, такое реинвестирование даст результат

ST=S0(l +i/m)mT.

Отсюда, пользуясь определением эффективной ставки, найдем ее зависимость от номинальной ставки /:

r =(1+JL)«-1. (1.5) J m

Таким образом, эффективная ставка измеряет тот относительный доход (ST= і — S0)/SQ, который может быть получен в целом за год, т.е. сторонам безразлично, применять ли ставку / при начислении процентов m раз в год или годовую ставку геу— и та и другая эквивалентны в финансовом отношении. Заметим, что при увеличении частоты капитализации m период начисления становится все меньше и мы приближаемся к непрерывному наращению процентов. В пределе при т, стремящемся к бесконечности, получим формулы непрерывного приведения (1.3) с силой роста 8, равной номинальной ставке / (8 = /). Пользуясь определением (1.4), найдем эффективную ставку, эквивалентную непрерывному наращению с силой роста 8: /у= еъ — 1. Отсюда следует,.

что 6 = ln(/yf 1), т. е. операция приведения (дисконтирования, нарашения) на п периодов по сложному проценту со ставкой ref равносильна приведению в непрерывном времени с силой роста 6.

Наращение процентов и инфляция. Инфляция проявляется в росте цен Pt и может измеряться темпом их прироста г, а также периодом Г, за который они удвоятся. Первый показатель называют темпом инфляции. Он характеризует относительное изменение цены за один период:

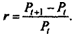Р,-Р0(1+*У.

Определим число лет Г, необходимых для двукратного подорожания. В этом случае

2 = (1 +г)г

т_п2 1001п2 г г\%

Для грубых прикидок числа лет удвоения можно воспользоваться правилом числа 70:

70 70 (1.6)

темп инфляции в процентах г\%

Это правило получается из формулы удвоения заменой 1п2 его приближенным значением: 1п2 » 0,7. Очевидно, что данные формулы можно использовать и для отрицательного темпа (г < 0), т. е. когда имеет место не прирост, а снижение.

В финансовой практике инфляцию учитывают, корректируя ставку начисления процентов таким образом, чтобы компенсировать обесценивание наращенной суммы из-за роста цен. Чтобы номинальная ставка J при годовой инфляции г соответствовала реальной ставке /, она должна удовлетворять условию

У = / + г+/г. (1.7)

При невысокой инфляции произведением в формуле (1.7) можно пренебречь. В этом случае поправка на инфляцию ограничивается величиной темпа г, и ставку корректируют по формуле

+ Л (1.8)