1.2. типовые примеры

1.2. типовые примеры

Правила простых и сложных процентов (1.1), (1.2) выражаются формулами, в которые входят следующие показатели: начальная сумма Р0, конечная сумма Рю процентная ставка начисления / или ставка удержания (учетная) j, промежуток времени п между исходной и замыкающей суммами Р0 и Рп. Итого четыре параметра. Пусть любые три из них заданы, тогда формула, соответствующая применяемому правилу и используемой ставке (начисления или учетной), дает уравнение для отыскания недостающего параметра при известных трех. Возникающие при этом четыре варианта задач для случая начисления по ставке / представлены в табл. 1.1.

Разумеется, при переходе на учетную ставку j типы задач будут те же, изменятся лишь базовые формулы, необходимые для их решения.

1. Отыскание наращенной суммы,

В какую сумму обратится через 5 лет долг, равный 10 тыс. руб., при росте по сложной ставке 5,5\%? Чему равны процентные деньги?

Примечание. Под процентными деньгами, или, кратко, процентами, понимают величину прироста денежной суммы: /„ = Рп — Р0.

Решение

/>5= 10000(1 + 0,055)5 = 10000 • 1,30696 « 13070; /„= 1307010000 = 3070.

Отыскание современной величины.

Сумма в 5 млн руб. выплачивается через 5 лет. Какова ее современная величина при условии, что применяются сложные проценты по ставке 10\% годовых?

Решение

/>0= 5 • 106(1 + 0,1Г5 = 5 • 106 0,620921 = 5 • 620921 = 3104605.

Отыскание срока приведения.

Каким должен быть срок ссуды в днях, для того чтобы долг, равный 100 тыс. руб., вырос до 120 тыс. руб. при условии, что начисляются простые проценты по ставке 25\% годовых?

Решение

100-(1 +л0,25) = 120.

4

Откуда п = года или в днях: 5

л = 365~ = 292 дня.

Отыскание ставки начисления.

При двух одинаковых процентных повышениях заработная плата с 10 тыс. руб. обратилась в 12544 руб. Определите, на сколько процентов повышалась она каждый раз?

Решение

12544= 10000 -(1 + О2.

Откуда

Л . /12544 112 , Л„

1 + /= / = = 1+0,12,

V ЮООО 100

и поэтому/= 12\%.

Для переменной во времени процентной ставки базовые формулы (1.1), (1.2) переписываются с учетом их изменения на присоединяемых периодах.

Переменные процентные ставки.

Клиент положил в банк 10 тыс. руб. сроком на один год. Согласно депозитному договору годовая процентная ставка до середины второго квартала составляет 30\%, далее до конца третьего квартала — 25\%, а с начала четвертого квартала — снова 30\%.

Какую сумму клиент получит в конце года при условии, что договор предусматривает начисление

а) по простым процентам;

б) по сложным процентам?

Решение

В этой задаче периоды начисления в долях года равны следующим значениям:

"і = «2 = XU + Уз= 3/g (года); пъ = У4 (года).

Подставляя их в формулу для простого процента, получим:

10000(1 + 3/8" 0,3 + 3/g • 0,25 + У4 • 0,3) = 12812,5 руб.;

аналогично для сложного процента будем иметь:

10000(1 + 3/8 * 0,3)(1 + 3/8 • 0,25)(1 + У4 • 0,3) = 13080,57 руб.

Приведем примеры, при решении которых можно воспользоваться понятием эффективной ставки.

Эквивалентная непрерывная ставка.

Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20\%? Решение

е5 = (1+0,2/4)4.

Откуда

6 = 41п(1 + 0,05) = 4 • 0,04879 = 0,19516 * 19,52\%.

Непрерывный сложный процент.

Пусть сила роста (непрерывный темп прироста) изменяется во времени по линейному закону

5, = 50 + а/,

где $0 начальное значение;

а годовой прирост (он может быть как положительным, так и отрицательным).

Получить формулу наращенной суммы S(t) при величине вклада S0. Решение

Согласно определению силы роста

= 50 + я/, или — = 80

5(0 0 S 0

Решая это дифференциальное уравнение с исходным условием S0, получим:

5(/) = 50е 2 ,

где #(/) = е 2 — множитель наращения.

8. Эффективная ставка как результат кратной капитализации.

Ежемесячный темп инфляции составляет 10\%. Рассчитайте

оценку годовой инфляции. Решение

Исходя из месячного темпа прироста цены найдем, опираясь на принцип капитализации, годовой индекс цены и годовой темп инфляции:

Ind = (l + 0,1)12= 3,1384, гГ0Д=Іпсі1 =2,1384, т.е. 213,84^.

9. Сравнение финансовых операций с помощью эффективной

ставки.

Что выгоднее: вложить 20 тыс. руб. на 1 месяц под годовую ставку 12\% или на 6 мес. под 12,2\%? Решейие

Найдем для каждого варианта эквивалентную ему эффективную процентную ставку:

г, = (1,01)121 = 0,1268 = 12,68\%; r2=(l,061)21 =0,1257= 12,57\%.

Очевидно, что из двух вариантов выгоднее тот, для которого эта ставка будет больше. В нашем случае это первый вариант, который и следует предпочесть.

Учет инфляции.

Какую ставку j должен назначить банк, чтобы при годовой инфляции 12\% реальная ставка оказалась 6\%? Решение

По формуле (1.7) требуемая номинальная ставка равна:

j = 0,06 + 0,12 + 0,6 • 0,12 = 0,1872 = 18,72\%.

Для получения приближенного решения можно воспользоваться оценкой (1.8) и прийти к достаточно точному значению:

7*0,06 + 0,12 = 0,18=18\%.

Правило числа 70.

Какой среднегодовой темп прироста валового внутреннего продукта (ВВП) обеспечит через 10 лет его удвоение? Решение

Для отыскания темпа х\% воспользуемся правилом числа 70, которое запишем в виде уравнения:

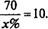
Откуда х = — = 7\%, иначе говоря, экономика в среднем должна расти на 7\% ежегодно, чтобы через десять лет произошло ее удвоение.