2.2. типовые примеры

2.2. типовые примеры

1. Наращенная сумма (простой процент).

Клиент сделал вклад на текущий счет в банке в сумме 100 тыс. руб. под простую ставку 14\% годовых. Затем через 3, 6 и 9 месяцев он вложил еще по 10 тыс. руб. В конце года клиент закрыл счет. Какую сумму он получил при закрытии счета?

Решить задачу, используя следующие правила.

Разделение счета на основной и процентный.

Мультисчет. Решение

1. В течение первого квартала сумма на счете капитала составляла величину Р = 100. Проценты за первый квартал (длительность квартала в долях года равна 0,25):

/А/ • Р= 0,14 • 0,25 • 100 = 3,5.

В течение второго квартала сумма на основном счете Р= 100 + + 10 = 110, проценты с которой равны:

/Аґ • Р = 0,14 • 0,25 110 = 3,85;

сумма на счете в течение третьего квартала — 120, проценты за третий квартал — 4,2; сумма на основном счете в течение четвертого квартала — 130, проценты равны 4,55. Итоговая сумма на процентном счете (проценты за год) определяется сложением поквартальных процентов и составляет величину /= 3,5 + 3,85 + + 4,2 + 4,55 = 16,1. Сумма, которую получит клиент при закрытии счета, равна 130 + 16,1 = 146,1 тыс. руб.

2. Величина вклада на накопительном счете на дату закрытия равна наращенной сумме потока всех вложений:

S=SX + S2 + S3 + S4;

5= 100(1 + 0,14) + 10(1 + 0,75 • 0,14) + 10(1 + 0,5 • 0,14) + + 10(1 + 0,25 • 0,14) = 146,1 тыс. руб.

2. Коммерческое и актуарное правила.

В условиях предыдущей задачи заменим вложение 10 тыс. руб. в конце 6-го месяца на изъятие в 20 тыс. руб. и найдем состояние счета на конец каждого квартала в зависимости от используемого банком правила (коммерческого или актуарного);

Решение

Согласно коммерческому правилу все платежи учитываются на счете капитала, и его последовательным состояниям соответствует вектор (ПО, 90, 100, 100).

Найдем последовательность сумм на процентном счете:

(3,5; 3,5 + 3,85 = 7,35; 7,35 + 0,14 • 0,25 • 90 = = 10,5; 10,5 + 0,14 • 0,25 • 100 = 14).

Сопоставляя эти последовательности, получим полную сумму счета на конец каждого квартала:

Sx= 113,5; 52= 97,35; 53= 110,5; 54= 114.

На практике банки выплачивают проценты по вкладу, поэтому в случае изъятия сумм сначала уменьшается процентный счет, а затем основной (актуарное правило). Согласно этой процедуре выплата в 20 тыс. руб. производится за счет накопленных за полугодие процентов (7,35) и снятия недостающей суммы (20 7,35 = = 12,65) с основного счета. В результате придем к следующим временным характеристикам состояний основного, процентного и полного счетов (Ph Ih St) (табл. 2.1).

3. Наращенная сумма (сложный процент).

Для создания резервного фонда ежегодно выделяется по 400 тыс. руб. На аккумулируемые средства начисляются сложные проценты по ставке 8\%. Необходимо определить общую сумму фонда через 5 лет для следующих вариантов поступления средств и начисления процентов:

а) поступление в конце квартала, начисление процентов поквартальное;

б) поступление в конце квартала, начисление процентов по

полугодиям;

в) поступления в конце года при непрерывном начислении

процентов;

г) поступления на протяжении всего срока происходят непрерывно, проценты начисляются непрерывно.

Решение

а) Воспользуемся формулой (2.2) для простой годовой ренты,

заменив год кварталом, а годовую ставку квартальной: / = 2\%,

п = 20. Значение коэффициента наращения s(20,2) = 24,297, отку24 297

да S = 400 .-=^=21 = 2429,7 тыс. руб.; 4

б) в этом варианте р = 4, т = 2, п = 5, — = 0,04. По формуле

т

(2.1) находим:

с 400 (1+0,04)10 -1

5 = ^ ■—— =2425,45 тыс. руб.;

4 (1 + 0,04)2/4-1

в) эквивалентный заданной годовой ставке / непрерывный процент: 6 = ln(l + 0,08) = 0,07696 (e°'07W6=l,08).

Наращение с силой роста 5 даст тот же результат, что и начисление под годовую ставку 8\%. Воспользовавшись формулой (2.2), найдем итоговую величину фонда:

S = 400 • j(5,8) = 400 • 5,8666 = 2346,64 тыс. руб.;

г) для случая (2.8) постоянной непрерывной ренты и непрерывных процентов будет накопленная сумма

с 400 (1,085-1) _ОГ1 .

S = — = 2439,33 тыс.руб.

0,07696

4. Современная стоимость ренты.

Какую сумму необходимо поместить в банк, чтобы иметь возможность в течение следующих 8 лет ежегодно снимать со счета 25 тыс. руб., исчерпав счет полностью к концу срока? Решить задачу для следующих вариантов начисления процентов:

а) в конце года по ставке / = 5\%;

б) в конце квартала при той же годовой ставке;

в) непрерывно с силой роста 5 = 5\%.

Решение

Во всех случаях требуется найти современную стоимость годовой ренты:

а) применим формулу (2.2): А = R • а (8,5). Значение а (8,5) =

= 6,46321. Откуда:

А = 25000 • 6,46321 = 161580,25 руб.;

б) по условию проценты начисляются 4 раза в год. Полагая в

формуле общей ренты р = 1, т = 4, п = 8, / = 0,05, найдем интересующее нас значение современной величины:

А = 25000.1-(1 + 0-°5/f4-8 =25000 =160965,75 руб.;

(1 + 0,05/4)4 -1 0,050945

в) в этом случае перейдем к эффективной ставке процента / =

= е6 1 и применим обобщающую характеристику (2.2) простой

годовой ренты. В результате получим формулу современной стоимости

(С8-1)

для расчета требуемой суммы:

1-0,058

А = 25000 -Ц^ = 160753,64.

5. Отыскание размера платежа.

Необходимо найти размер равных взносов в конце года для следующих двух ситуаций, в каждой из которых предусматривается начисление на взносы годовых процентов по ставке 8\%.

1. Создать к концу пятилетия фонд, равный 1 млн руб.

2. Погасить к концу пятилетия текущую задолженность, равную 1 млн руб.

Решение

а) приравняем размер создаваемого фонда наращенной сумме

(2.2) простой годовой ренты. Из полученного уравнения находим:

D S 1000000 .-мыл *

R = = = 170456,4 руб.

^(5,8) 5,86660096

Таким образом, ежегодные взносы в размере 170456,4 руб. достаточны при начислении на них процентов по указанной ставке для накопления 1 млн руб.;

б) для определения ежегодной суммы погашения за 5 лет текущего долга в 1 млн руб. приравняем его к современной величине ренты (2.2), члены которой погашают долг. Из полученного

уравнения находим:

D А 1000000 „ЛЛ*слс *

R = = = 250456,46 руб.

д(5,8) 3,99271

6. Отыскание срока ренты.

Иванов должен выплатить Петрову 40 тыс. руб. Он предлагает заменить эту разовую выплату ежегодными платежами в начале каждого года по 10 тыс. руб. каждый. Сколько лет должен будет ждать Петров полного погашения долга со стороны Иванова, если на долг начисляются проценты по ставке 8\% годовых?

Решение

Задача сводится к определению срока простой годовой ренты. Полагая в (2.2) приведенную стоимость А равной разности между величиной долга D и платежом R, придем к следующей формуле:

п =

ln(l + /)

Подставляя в нее исходные данные, получим:

-1п(1 -3000 -0,08/10000) 1п(1 + 0,08)

«3,57 года.

Пусть продолжительность заменяющей ренты равна 3 годам. Тогда ее современная величина

А3 = 10000 • а(3,8\%) = 10000 • 2,5771 « 25771.

В то же время современная величина заменяемой ренты А = = 30 тыс. Разность, таким образом, составляет 4229 руб. Эту сумму следует уплатить в начале первого периода заменяемой ренты или с соответствующим наращением в любой другой момент. Если заменяемую ренту продлить на один год, то для окончательного погашения долга Иванов должен будет в конце 4-го года выплатить Петрову сумму Л* = 4229 • 1,084 = 4229-1,3605 «5753,55 руб.

7. Отыскание ставки процентов.

Банк предлагает клиенту выплату ренты на следующих условиях: клиент вносит 10 тыс. руб., а банк в течение 5 лет выплачивает ему в конце каждого года по 3 тыс. руб. Определить доходность подобной операции.

Решение

Современная стоимость А получаемой клиентом ренты, вычисленная по искомой процентной ставке /, совпадаете величиной его начального капитала. При известных значениях/! = 10, R = 3,

п = 5 найдем я(5,/) = -у= 3,(3). В соответствии с таблицей коэффициентов приведения годовой ренты я(5; 15,5) = 3,3128<я(5,/) = = 3,(3) < я(5; 15) = 3,3522. Поэтому за приближенную оценку доходности допустимо принять среднюю табличных ставок: / *

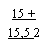= 15,25\%.

8. Замена ренты разовым платежом (правило мулътисчета). Два платежа Sx = 100 тыс. руб. и *У2 = 50 тыс. руб. со сроками 150 и 180 дней, отсчитываемыми от одной базы, заменяются одним со сроком 200 дней. Стороны согласились на замену при использовании простой ставки, равной 6\% годовых. Найти величину консолидированного платежа Sz. Решение

Для замены ренты Su S2 платежом Sz можно воспользоваться моделью мультисчета: финансово-эквивалентный заменяющий платеж должен равняться сумме наращений выплат S{, S2 за период их отсрочки:

Sz = 100(1 + 0,06 • 50/365) + 50(1 + 0,06 • 20/365) = 150986 руб.

9. Отыскание срока платежа, заменяющего ренту.

Рассматриваются два варианта перечисления суммы 1,2 млн руб.: платежами в конце года с приростом в 5 тыс. руб. на протяжении 16 лет или разово. Найти срок т однократного платежа при условии, что ставка сложного процента равна 8\%.

Решение

Применяя (2.4), запишем условие эквивалентности в виде равенства наращенных сумм по каждому варианту:

(Rl+°).s(nU)-—=Л(І4-/ГТ.

Согласно условиям задачи R = 12000000, а = 5000, п = 16, / = 0,08. Для определения недостающего параметра R{ (первого платежа) воспользуемся формулой суммы п членов арифметической прогрессии:

l^+djn-])

Sn= 2~'"'

или, в обозначениях задачи:

1200000 = 2*'+500° 15-16. 2

Решая, получим R{ = 37500. Заменим параметры в алгебраической записи условия эквивалентности их численными значениями. В результате придем к следующему уравнению относительно т:

(37500 + ^М16;8)-!^^=1200000 -1,08і6-. 0,08 0,08

Откуда следует, что 1,08т = 2,02277 и т = ш*>ш" w915 Г()да

lnl,08

Объединение рент.

Найти годовую ренту-сумму сроком в 10 лет для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, другая 8 и 800. Годовая ставка 8\%.

Решение

Для отыскания современной величины ренты-суммы определим числовые значения одноименной характеристики для рент-слагаемых:

Ах = 1000 ■ в(5; 8) 1000 • 3,993 = 3993; А2 = 800 • в(8;8) = 800 • 5,747 = 4598.

Значит, у ренты-суммы современная величина

^ = ^+^2*8591.

Согласно формуле (2)

Az = Ra(lQ;8). Следовательно, годовой платеж ренты-суммы:

^ = Ve(10;8),

или, в числах:

Ry= 8591/6,710= 1280,328.

Замена ренты (сложный процент).

Заменить годовую десятилетнюю ренту с годовым платежом 1000 евро на ренту с полугодовым платежом по 600 евро. Годовая ставка 10\%, проценты начисляются в конце периодов ренты.

Решение

Согласно требованию эквивалентности современные величины рассматриваемых финансовых потоков одинаковы, т. е.:

А2 = А{= 1000 я(10; 10) = 1000 . 6,1446 = 6144,6.

Для заменяющей ренты начисление процентов и платежи производятся два раза в год, поэтому для нее можно использовать те же формулы (2.2), что и для простой годовой ренты, считая единичным периодом времени полугодие со ставкой начисления 5\%. Отсюда получим уравнение для длительности п этого потока:

Л2=6ОО-0(я; 5),

т. е.

Это значение заключено между двумя табличными: д(14;5) = = 9,899 и д(15;5) = 10,380. Поэтому за приближенную оцен14+15 1„ С

ку можно принять величину п = = 14,5 периода, или

7,25 года. 2