§ 3. риск портфеля

§ 3. риск портфеля

Итак, мы установили, что ожидаемая доходность портфеля акций представляет собой взвешенную среднюю доходность акций, входящих в портфель. Однако задача формирования портфеля акций заключается в том, чтобы учесть не только значения доходности, но и степень риска входящих в портфель акций, которую, как было показано раньше, можно измерить с помощью стандартного отклонения. Продолжим наш пример с акциями А и В и вычислим стандартное отклонение портфеля из двух этих акций. Для вычисления имеется следующая информация об акциях А и В. Стандартные отклонения этих акций, рассчитанные по итогам предыдущих лет, составляют, соответственно, 10\% и 60\%. Предположим, что портфель состоит из 40\% акций А и 60\% акций В.

Первое, что можно предположить, это допустить, что стандартное отклонение доходности портфеля есть взвешенная средняя стандартных отклонений для индивидуальных акций:

10 х 0,4 + 60 х 0,6 40\%.

Этот результат был бы правильным, если бы цены на акции и, соответственно, их доходности двигались в совершенно одинаковом направлении — при росте одной акции точно так же вела бы себя и другая акция. В действительности, как правило, дело обстоит иначе, поэтому риск портфеля не является взвешенной средней стандартного отклонения индивидуальных акций в портфеле. Для объяснения процедуры вычисления риска портфеля, состоящего из двух акций, составим следующую таблицу (рис. 12.2).

Дисперсия этого портфеля — это сумма значений величин всех четырех клеток. Чтобы заполнить верхнюю левую клетку, нужно взять произведение дисперсии акции А и квадрата доли инвестиций в акцию А. Аналогичным образом заполняется нижняя правая клетка, т. е. значения в этих клетках зависят от величины дисперсии акций А и В.

Запись в две другие клетки зависит от ковариации акций А и В. Ковариация может быть выражена как произведение стандартных отклонений двух акций и коэффициента корреляции:

<*м> = алховхСогм, (12.2)

где аАВ — ковариация акций А и В (CovAB) (СогАВ) — коэффициент корреляции акций А и В.

Если в верхней левой и нижней правой клетках мы «взвешивали» дисперсию посредством квадрата долей инвестированных в соответствующие акции (w,w), то в оставшихся двух клетках, когда мы имеем дело с ковариацией, «весами» является произведение двух долей соответствующих акций (wA,wB).

Дисперсия портфеля АВ будет равна сумме слагаемых всех четырех клеток таблицы:

°р =caxwa +Glxwl +2(о,, ха вхш*лха>ЕхСоглв).

Что касается стандартного отклонения портфеля, то оно есть не что иное, как квадратный корень из дисперсии:

Как следует из приведенных выше формул, стандартное отклонение портфеля зависит от: величин стандартных отклонений, входящих в портфель акций, долей инвестиций в каждую акцию, и кова-риаций (или коэффициентов корреляции) акций.

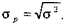Коэффициенты корреляции двух акций отражают поведение этих акций. Если акции имеют свойство «двигаться» в одном направлении (т.е. если цена одной акции идет вверх, то растет курс и другой акции), то коэффициенты корреляции и ковариации позитивны. Если курсы акций двигаются в разных направлениях, то коэффициенты корреляции и ковариации негативны. Если бы движение акции было полностью независимо друг от друга, то коэффициенты корреляции и ковариации были бы равны нулю.

В приведенном выше примере был показан метод расчета стандартного отклонения портфеля, состоящего из двух акций. Однако этот метод применим для расчета стандартного отклонения любого портфеля. В таком случае нам необходимо заполнить таблицу с большим числом клеток (рис. 12.3).

N

7<-

Рис. 12.3. Ковариационная матрица для определения дисперсии портфеля

Каждая диагональная клетка содержит дисперсию, взвешенную на долю инвестиций в данную акцию, возведенную в квадрат (Gf х W? у

ходкость и стандартное отклонение портфеля, а также представим эти данные графически (рис. 12.4).

Норма прибыли и стандартное отклонение акций С, D и портфеля CD

Среднегодовую доходность и стандартное отклонение находим по формулам (11.59) и (11.58):

20-5 + 15-10 + 30

о =

= 10\% ,

_ |(20-10)2 + (-5-10)г +(15-10)2 +(-10-10)2 +(30-10)г _

= 16,2\%.

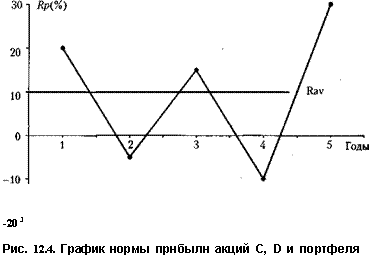Как показано на рис. 12.4, графики движения значений доходности акций, имеющих строго позитивную корреляцию, полностью совпадает с графиком доходности портфеля, составленного из этих акций.

Если допустить, что коэффициент корреляции двух акций равен -I, риск портфеля может быть полностью исключен. Данные об акциях Е и F и портфеле EF представлены в табл. 12.3, а графики доходности — на рис. 12.5.

40 30 20 10 О

-10 '

1 ^'2

Акция F /

f ч^ Портфель

/

З 4 Акция х /

V

-20

Рис. 12.5. Графики доходности акций Е, F и портфеля EF

Графики показывают, что доходность портфеля остается постоянной (10\%) несмотря на значительные колебания доходности входящих в портфель акций Е и F. Стандартное отклонение портфеля равно нулю. Это — безрисковый портфель.

В действительности акций, которые имеют абсолютно негативную корреляцию (Сог= -1), не существует. Подавляющее большинство акций имеют позитивную корреляцию. Так, в среднем коэффициент корреляции для двух случайно выбранных акций, которые котируются на Нью-Йоркской фондовой бирже, составляет +0,6. При таком раскладе комбинация акций в портфеле снижает риск, но не исключает его полностью.

Предположим, что коэффициент корреляции акций А и В, которые рассматривались ранее, равен +0,6.

Доли акций А и В, доходность (Rp) и стандартное отклонение портфеля АВ (ор)

Доходность портфеля акций АВ в зависимости от различного сочетания долей акций А и В была представлена в табл. 12.1. Рассчитаем стандартное отклонение портфеля АВ при различных сочетаниях долей акций А и В. Результаты расчетов представлены в табл. 12.4, а на рис. 12.6 приведена кривая взаимосвязи стандартного отклонения и доходности портфеля в зависимости от изменения долей акций А и В в портфеле.

Если бы коэффициент корреляции акций А и В был равен 1, то стандартное отклонение портфеля было бы выше, чем при коэффициенте корреляции, равном 0,6, а линия, соединяющая точки А и В на рис. 12.6, превратилась бы в прямую линию. (На рис. 12.6 она показана пунктиром.)

Представленные выше расчеты и графики позволяют сделать следующие выводы:

* доходность портфеля есть взвешенная средняя значений доходности входящих в портфель акций (весами служат доли инвестиций в каждую акцию);

• если акции ведут себя совершенно одинаково (Q, = +1), то стандартное отклонение портфеля остается таким же, как у входящих в портфель акций;

О 10 20 30 40 50 60 °Р(\%)

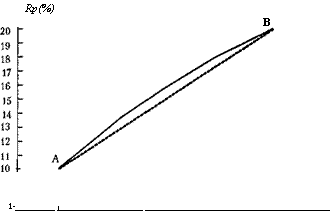Рис. 12.6. График взаимосвязи стандартного отклонения и доходности

портфеля АВ

риск портфеля не является средней арифметической взвешенной входящих в портфель акций; портфельный риск (за исключением крайнего случая, когда Сиг = +1) будет меньше, чем средняя взвешенная стандартных отклонений, входящих в портфель акций;

при достижении коэффициентом корреляции определенного значения можно достичь такого сочетания акций в портфеле, что степень риска портфеля может быть ниже степени риска любой акции в портфеле;

наибольший результат от диверсификации может быть получен от комбинаций акций, которые находятся в негативной корреляции; если коэффициент корреляции двух акций равен -1, то теоретически из пар таких акций можно сформировать безрисковый портфель (со стандартным отклонением, равным нулю);

в действительности негативная корреляция акций почти никогда не встречается, и безрисковый портфель акций сформировать практически невозможно;

риск портфеля может быть снижен за счет увеличения числа акций в портфеле, при этом степень снижения риска зависит от корреляции добавляемых акций; чем меньше коэффициент корреляции добавляемых акций, тем значительнее снижение риска портфеля.