2.4. краткосрочные долговые обязательства

2.4. краткосрочные долговые обязательства

В этом параграфе более подробно рассмотрим описание кредитных сделок с некоторыми простейшими финансовыми инструментами — краткосрочными долговыми обязательствами. Краткосрочные долговые обязательства — один из распространенных видов ценных бумаг, обращающихся на так называемом денежном рынке (money market). Денежный рынок — рынок краткосрочных ценных бумаг со сроком обращения не больше года. Наиболее типичными представителями таких ценных бумаг являются депозитные сертификаты и векселя.

До сих пор наши определения процентных и учетных ставок (за период и нормированных) были привязаны к отдельным сделкам. Это ставки именно сделок, а не класса. Для отдельных сделок процентная или учетная ставка (за период и нормированная) —просто еще один параметр. Выше отмечена важная роль процентной ставки как регулятора кредитного рынка. Эта роль связана с массовостью кредитных сделок. Существуют ли на практике классы сделок, в которых определяющей является учетная ставка? Оказывается, такой класс сделок действительно существует. Он тесно связан с наличием, во-первых, специальных дисконтных долговых инструментов и, во-вторых, с операцией учета векселей. В этом параграфе мы кратко коснемся роли процентной и учетной ставок для обращающихся долговых обязательств — одного из видов финансовых инструментов.

Кредитная сделка может быть реализована в виде прямого кредитного договора (контракта) между двумя сторонами (кредитором и заемщиком). Такой контракт на все время своего действия неразрывно связан с заключившими его сторонами и является, вообще говоря, необращающимся долговым обязательством. Получение предприятием кредита в банке, оформление депозитного договора между вкладчиком и банком — примеры таких контрактов. Однако во многих случаях кредитная сделка осуществляется посредством эмиссии (выпуска) и продажи обращающихся долговых обязательств. В отличие от прямого контракта эти обязательства представляют собой ценные бумаги, которые относительно легко могут менять своих владельцев. Если это именная ценная бумага, т.е. ее владелец в каждый момент явно указан (в самой бумаге), то обращение осуществляется с помощью определенного механизма передачи прав. Если это ценная бумага на предъявителя, то обращение ее на рынке осуществляется свободной куплей/продажей.

Когда кредитная сделка представлена долговым обязательством — ценной бумагой, то основные параметры сделки содержатся в ней в качестве обязательных реквизитов. Так, начало сделки отмечается датой эмиссии, конец — датой погашения. Финансовые параметры устанавливаются специфическим для каждого вида долгового обязательства образом.

В так называемых дисконтных ценных бумагах обычно фиксируется полная сумма (сумма погашения) долга. При погашении обязательства его владелец получает от эмитента указанную сумму. Доход владельца обязательства (инвестора) образуется за счет того, что покупка обязательства осуществляется по цене ниже суммы погашения, т.е. в процессе обращения дисконтная ценная бумага продается с дисконтом (скидкой). Фиксированная полная (возвращаемая) сумма долга — основной финансовый параметр дисконтных ценных бумаг, часто называемый номиналом.

Наиболее распространенным примером дисконтных ценных бумаг являются векселя. Нормативные (юридические) характеристики векселя и условия его обращения регламентируются специальным законодательством. Имеются различные типы векселей, например простые и переводные. Отвлекаясь от специфических особенностей различных видов, в рамках математической модели можно описать вексель его реквизитами (обязательными параметрами). Вексель характеризуется:

номиналом JF(Face Value);

датой эмиссии Г0;

датой погашения t{ или сроком обращения Т0.

В этом описании векселя никаких процентных ставок не указывается. В некоторых разновидностях векселей задание ставки подразумевается [25]. Однако в классическом случае это чисто дисконтный инструмент, содержащий всего один финансовый параметр — номинал F, который всегда является суммой погашения. Другими словами, именно эту сумму в день погашения t{ получит владелец векселя, купивший его по некоторой (естественно меньшей, чем номинал) цене Р, либо в день эмиссии, либо в некоторый другой день до даты погашения.

В финансовой практике многих стран широко распространен еще один вид дисконтных ценных бумаг, весьма похожих на векселя, эмитент которых — правительство (обычно министерство финансов или казначейство). В США эти краткосрочные дисконтные бумаги так и называются Казначейскими векселями (Treasure Bills). В нашей стране они известны под названием ГКО (государственные краткосрочные облигации). Их эмитентом является Министерство финансов РФ. Номинал ГКО составляет .Ж ООО. По этой цене облигация погашается. Инвесторы покупают ГКО на финансовом рынке (точнее, на рынке ГКО) по цене, меньшей номинала. На рынке цена ГКО задается в виде курса (или котировки) на данный момент времени (текущий курс), который выражается в процентах от номинальной стоимости облигации. Так, курс 75 означает, что цена (в рублях) составляет -#750. В терминах котировок учетная ставка (в \%) представляет собой просто разность между номиналом (100) и текущим курсом (Q).

В процентных бумагах [26, 27] обычно фиксируются основная сумма долга и процентная ставка (купонная). К такому виду долговых обязательств относятся, например, депозитные сертификаты, эмитируемые банком. Основная сумма долга в депозитном сертификате фиксируется в виде номинала, т.е. номинальной стоимости этой бумаги. В момент эмиссии депозитный сертификат обычно продается инвестору (кредитору) по номинальной стоимости. При его погашении банк выкупает сертификат у владельца (инвестора) по цене выше номинала. Цена погашения больше номинала на сумму начисленных процентов за полный срок обращения сертификата.

Выпишем основные финансовые и временные параметры (реквизиты), связанные с денежным сертификатом:

F — номинал;

tQ — момент (дата) эмиссии; г, — момент (дата) погашения;

Го" г«бр= ('і ~ У — период обращения;

с — купонная (нормированная процентная) ставка.

Введенные параметры — модельные. Так, все временные параметры должны указываться в некоторой выбранной временной (например, годовой) шкале. На практике моменту tQ соответствует дата эмиссии; моменту t — дата погашения. Срок обращения Тп задается в днях — /)0. Поэтому для получения значений временных параметров в модели необходимо предварительно выполнить преобразование календарных (практических) данных в модельные (теоретические) по однму из временных правил (см. §1.6). Такое преобразование осуществляется обычно по формуле

(2.28)

где D0 — срок сделки в днях; Y— годовой дивизор.

С долговыми обязательствами любого вида (векселем или сертификатом) естественным образом связана так называемая стандартная кредитная сделка, заключающаяся в том, что инвестор приобретает обязательство в момент эмиссии и держит его до погашения. В этом случае реквизиты долгового обязательства будут играть роль основных параметров сделки. Началом сделки (г0) служит момент эмиссии, концом (t{) — момент погашения обязательства. Для процентных бумаг в этом случае номинал (F) задает начальную стоимость (51), а для дисконтных — конечную стоимость (S{) долга. Если в процентной бумаге фиксируется процентная ставка, то конечная сумма долга вычисляется по ней и номиналу. Если же некоторый параметр не указан в виде реквизита, то он определяется внешними (рыночными или договорными) условиями.

Естественность подобных сделок вовсе не означает их наибольшую распространенность. На практике обращающиеся ценные бумаги редко имеют постоянного владельца в течение всей своей «жизни», они покупаются и перепродаются многократно. Так, владелец векселя, нуждающийся в наличных средствах, может учесть вексель в банке. Учет банком векселя означает покупку банком векселя у его владельца. Цена такой сделки или учетная (выкупная) цена векселя, естественно, ниже его номинала, т.е. вексель учитывается с дисконтом. Процент, который составляет дисконт (скидка) по отношению к номиналу, есть, очевидно, не что иное, как учетная ставка сделки. Само название этой ставки происходит от названия сделки. Таким образом, с одной и той же ценной бумагой на протяжении ее жизни осуществляется множество сделок, связь параметров которых с реквизитами самой ценной бумаги далеко не очевидна, хотя последние во многом определяют эти параметры.

Тем не менее анализ «естественной» (канонической) сделки полезен даже в тех случаях, когда инвестор, приобретая ценную бумагу, не намеревается держать ее до погашения. Такой анализ может служить эталоном для сравнения с другими сделками с данной ценной бумагой, например ее продажей до срока погашения.

Рассмотрим примеры простейших расчетов, связанных с депозитными сертификатами и векселями. Начнем с депозитных сертификатов.

Для депозитного сертификата купонная ставка с есть не что иное, как процентная ставка стандартной сделки с сертификатом, т.е. простой кредитной сделки, в которой кредитор покупает в момент г0 сертификат у эмитента по номиналу f и в конце срока t погашает (возвращает, продает) сертификат у эмитента, получая от него сумму погашения 5= Snm. Эти условия однозначно определяют сумму погашения через основные реквизиты сертификата:

S=F(+cT0). (2.29)

В этой сделке, как отмечалось, начальный покупатель сертификата является кредитором, а эмитент сертификата —должником, поскольку покупка сертификата по номиналу Fозначает передачу суммы /"эмитенту, который по окончании срока обращения Г0 обязан вернуть эту сумму вместе с процентами по ставке с, т.е. выплатить сумму погашения.

Пример 2.9. Пусть инвестор покупает (по номиналу) депозитный сертификат с номиналом Л 1000, купонной ставкой 20\% годовых и сроком обращения 270 дней. Найти сумму погашения сертификата. Использовать правило АСТ/365.

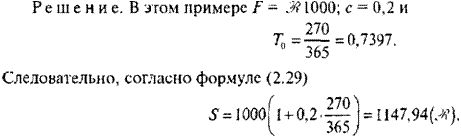Отметим, что реквизиты сертификата, как и определяемая ими сумма погашения, не изменяются в течение его периода обращения. Однако оставшийся срок до погашения в отличие от периода обращения Г0, безусловно, меняется с течением времени. Так, если сертификат был выпущен в момент tQ = 0 на срок Т0, то в некоторый более поздний момент времени г оставшийся срок до погашения есть

і 10 «.

(2.30)

Как уже говорилось, на равновесном рынке нормированные процентные ставки по различным сделкам близки к общему (одному и тому же) уровню. В частности, будут равны нормированные ставки сделок с различными долговыми инструментами, поскольку эти ставки представляют собой ожидаемые доходности, которые обеспечат себе инвесторы, покупающие эти инструменты. При этом имеется в виду, конечно, нормированная доходность к погашению, т.е. доходность за период от момента покупки до момента погашения. Следовательно, рыночные цены долговых инструментов будут устанавливаться таким образом, чтобы доходность по ним соответствовала равновесному уровню процентных ставок. Поэтому изменение уровня процентных ставок по каким-либо причинам, например вследствие роста темпов инфляции, приведет к изменению текущей цены депозитного сертификата. Но даже если уровень процентных ставок меняться не будет, цена сертификата тем не менее изменится, поскольку меняется оставшийся срок до погашения. Цена сертификата будет меняться так, чтобы доходность за оставшийся срок до погашения оставалась равной значению рыночной ставки процента.

1 На практике речь может идти лишь о близости к некоторому равновесному уровню, В теоретическом анализе говорят о точном равенстве. Считается, что пена эмиссии совпадает с номиналом, что все доходности в точности равны рыночной ставке и т.д.

Рассмотрим вопрос о связи цены и рыночной процентной ставки более подробно. В момент эмиссии депозитный сертификат продается обычно по цене, близкой к номиналу1. Это связано с тем, что эмитент устанавливает купонную ставку на уровне, равном рыночной ставке процента. В самом деле, ему нет смысла платить более высокую, чем рыночная, ставку, с другой стороны, он не может установить ее (при прочих равных условиях) меньше уровня ставки по другим альтернативным кредитным инструментам (банковским депозитам, векселям и т.д.), так как инвесторы (кредиторы) будут предпочитать инструменты с более высокой процентной ставкой (доходностью).

Если сертификат продается по номиналу, то ставка стандартной сделки, т.е. покупки и хранения до погашения, будет равна рыночной

ставке кредита: . .

= S-F = F(l + cT0)-F

Точно так же цена сертификата с течением времени должна меняться так, чтобы в каждый момент времени ставка по стандартной сделке (купить и держать) за оставшийся период до погашения была равна рыночному уровню ставки:

S -Р

пог рын /л -jf\

'рын ~ р Т ' \£.J£) рын пог

где / — рыночная нормированная процентная ставка; Т = Тпог — оставшийся срок до погашения; Р= Р — рыночная цена сертификата; S= Snor — сумма погашения сертификата. Отсюда „

P^=T-f~--PK{Smr) (2.33)

рын пог

или, опуская подразумеваемые индексы,

Р = (2.33') 1 + /Т

Таким образом, рыночная цена сертификата является текущей стоимостью (приведенной к текущему моменту) суммы погашения 5пог по рыночной ставке.

Пример 2.10. Пусть депозитный сертификат с номиналом ;>П000, купонной ставкой 15\% годовых и сроком обращения 180 дней продан за 70 дней до погашения. Если годовая рыночная процентная ставка в момент продажи составляла 10\%, то какова цена продажи сертификата? Использовать банковское правило АСТ/360.

Решение. Выразим сначала указанные в днях сроки в годовой шкале согласно банковскому правилу:

Т = Т = — = 0 5

70

Т = Т = = 0,1944.

"ог 360

( 180 ^

5 = 5 =1000 1 + 0.15

Сумма погашения сертификата составит

= 1075(.^).

!ЮГ л ' 360

Поскольку рыночная ставка / = 0,1, то текущая рыночная Р = Р цена сертификата

;> = -£-а 1075 ъ = Ю54,49(.*).

Заметим, что владелец сертификата, продавший его за 70 дней до погашения, реализует, вообще говоря, совсем другую процентную ставку сделки. Если он, например, купил сертификат по номиналу в момент эмиссии и продал его по найденной выше цене Р, то процентная ставка сделки за период владения сертификатом

Гы= 180 70 = ПО (дней)

составляет

1054 49 г = ~/' -1 = 0,05449, 1000

т.е. 5,45\%. Соответственно нормированная по банковскому правилу ставка сделки

0,05449 365

/ = __Ц— = 0,05449 -0,1808,

11 110/365 ПО

т.е. 18,08\%, что больше, чем доходность к погашению, равная рыночной ставке 10\%, которой обладает сертификат в момент его покупки новым владельцем.

F р s Таким образом, при досрочной продаже сертификата, т.е.

^1 ^ его продаже до срока погашеt t t ния, возникают, по существу,

7"вл гпог Непоследовательные простые

Рис 2 4 кредитные сделки. Первая осуществляется первоначальным владельцем сертификата, купившим его в момент эмиссии tQ по номиналу F и продающим его в момент t по рыночной цене Р, а вторая сделка осуществляется новым владельцем сертификата, который покупает его по рыночной цене Р в момент г и затем погашает его в момент погашения Диаграмма такой пары сделок изображена на рис. 2.4. Здесь Гм — срок владения сертификатом первым владельцем; 7*пог — оставшийся срок до погашения в момент покупки/продажи сертификата, совпадающий со сроком владения сертификатом вторым владельцем. Наконец, полный срок обращения Т — сумма указанных сроков:

обр вл пог

S-P 1

Заметим, что рыночный уровень процентных ставок определяет ставку именно второй сделки с периодом, оставшимся до погашения. Поэтому доходность за период до погашения, которая гарантируется инвестору, купившему сертификат по цене Р, называется (простой нормированной) доходностью к погашению сертификата. Она определяется, естественно, выражением

1

пог

(S Л

(2.34)

РТ Т{Р j

идентичным (2.32). Различие состоит лишь в интерпретации. Выражение (2.32) — исходное для получения формулы (2.33) цены сертификата по известной рыночной ставке (т.е. по известной доходности), тогда как (2.34) служит формулой вычисления доходности к погашению по известной (в момент г) рыночной цене Р сертификата.

Таким образом, цена и доходность к погашению взаимно определяют друг друга. В частности, рост процентных ставок і ведет, согласно (2.33), к снижению цены сертификата и обратно, рост цены Р сертификата ведет к снижению его доходности. Это общая закономерность соотношения цены и доходности долговых обязательств.

Перейдем к примерам расчетов с дисконтными ценными бумагами.

П р и м е р 2.11. Инвестор приобрел облигацию (ГКО) на аукционе по курсу Q{j = 75. Облигация погашается через 3 мес. Инвестор ожидает, что через 2 мес. курс облигации поднимется до Qt = 92. Что выгоднее по доходности: держать облигацию до погашения или продать ее через 2 мес. по ожидаемому курсу? Найти процентные и учетные (годовые и месячные) ставки для этих сделок.

Решение, Рассмотрим сначала (стандартную) сделку, когда облигация держится до погашения. В этом случае курс (0О) облигации задает начальную стоимость 5(). Поскольку номинал облигации (F) равен S ~ .#1000, то цена облигации, соответствующая курсу 75, равна

S0 = С?„ • F =0,75-1000 750( .Щ. Так как облигация погашается по номиналу, то конечная стоимость сделки

Sl = 1000(.#).

Проценты и соответственно дисконт за 3 мес. (до погашения) составят

l-D = Sx-S^ = 1000 750 = 250( .#). Процентная ставка за период до погашения

1 250 ПГЇП

/• = — ■ = 0,3333,

S{> 750

или 33,33\%, а учетная ставка

D 250

w = — = = 0,25,

S, 1000

т.е. 25\%.

Соответственно годовая процентная ставка сделки

,■ '= 0^3 = ,,3332,

ГОД 1 / ^

или f33,32\%, а месячная процентная ставка составит

w = —=-4—=t 0,1Ш,

_= 0,3333

или 11,11\%. Годовая учетная ставка

w 0,25

тл~ Т> " 1/4 ^

или 100\%. Здесь Т = 1/4 — срок в годах. Наконец, месячная учетная ставка

^=^ = ■^-0,0833,

міх

или 8,33\%.

Рассмотрим теперь сделку с продажей до срока погашения. В этом случае начальная сумма сделки Sa также задается курсом QQ:

^ = 750(^),

конечная сумма 5, определяется курсом Qv так что

5, = О, F= 0,92-1000 920(.#). Процент (дисконт) за 2 мес. составит

Г = 920 750 = 10(М), а процентная и учетная ставки за этот период

170 170 г' = — = 0,2267 и tv'= 1^1 = 0,1847, 750 920

т.е. 22,67 и 18,47\% соответственно.

Годовая процентная ставка сделки составит

_ г' 0,2267

или 136\%, а годовая учетная ставка

с=л1=М!£ = и082,

7» 1/6

или 110,82\%. Наконец, месячная процентная ставка

0,2267

MIX Л

■* час

или 11,34\%, а месячная учетная ставка этой сделки составит

d' =

w

Т

0,1847 2

= 0,0924,

или 9,24\%. Здесь Гмч. = 2 задает срок сделки в месяцах.

Таким образом, доходность первой сделки (133,32\%) ниже, чем доходность второй (136\%). Поэтому вариант с продажей до погашения выгоднее. Заметим, что подсчитанная доходность второй сделки есть лишь ожидаемая (или условная) доходность. Она станет реализованной, если курс облигации действительно вырастет за 2 мес. до 92. в отличие от этого доходность к погашению является гарантированной, поскольку облигация погашается по номиналу, а риск непогашения государством своих обязательств считается пренебрежимо малым'.

Итак, имеются два типа кредитных сделок: те, в которых базовым финансовым параметром является начальная сумма долга, и те, в которых эту роль играет конечная (полная) сумма долга. Первые назовем процентными, а вторые — дисконтными. Конечно, такое разделение имеет смысл лишь для класса сделок, а не для индивидуальных сделок. Определенный ранее простой класс — это класс процентных сделок. Коротко назовем его простым процентным классом. Совершенно аналогично можно определить простой класс дисконтных сделок или простой дисконтный класс: класс кредитных сделок назовем простым дисконтным классом, если нормированная учетная ставка для всех сделок этого класса одинакова. Все сделки такого класса назовем просто дисконтно-эквивалентными, а общее значение нормированных учетных ставок для сделок из этого класса — учетной ставкой класса.

1 Так традиционно считается. Недавний печальный опыт отечественного рынка ГКО заставляет относиться к такого рода утверждениям с осторожностью.

Естественно, для всех сделок дисконтного класса выполняются соотношения (2.20) (2.23), в которых d — нормированная учетная ставка класса. Формулы (2.24) и (2.25) также применимы ко всем сделкам класса. Однако вычисленные по этим формулам значения процентных ставок будут различными для разных сделок. Это относится, конечно, и к нормированной процентной ставке /'. Как показывает формула (2.25), нормированная процентная ставка / при фиксированной учетной ставке dзависит явным образом от срока сделки. Иными словами, две дис-контно-эквивалентные сделки не обязательно будут просто (процентно) эквивалентными. Однако если сроки этих сделок совпадают, то дисконтная эквивапентность влечет процентную. Верно, разумеется, и обратное утверждение, т.е. простая процентная эквивалентность в общем случае не влечет дисконтную эквивалентность, однако для сделок с одним и тем же сроком оба типа эквивалентности совпадают

Пример 2.12. Банк учитывает два векселя: один с номиналом .>?900 и сроком до погашения 3 мес, а другой с номиналом .#1500 и сроком до погашения 6 мес. Оба векселя учитываются по одной учетной ставке 20\% годовых. Найти учетные суммы векселей, доход и процентные ставки, которые реализует банк при погашении учетных векселей.

Решение. Учетная цена первого векселя

Рх = 900^10,2 — j = 855(.#),

учетная цена второго —

Рг =150o|i-0,2-ij=T350(.*?).

При погашении первого векселя банк получит доход

/, = 900 855 = 45 (/#). Следовательно, процентная ставка за 3 мес. составит

45

г = — = 0,0526, 1 855

а годовая ставка

_ _Jj_ аг ~ г) о) 1 1/4 ] ' '

или 21\%.

При погашении второго векселя доход составит

/, = 1500 1350 = 150( ,■■*?),

процентная ставка за 6 мес.

Л =~ = 0.1 Ш, 1350

а годовая ставка

/, =-^= 2-г, =0,2222, '1/2 2

или 22,22\%.

Таким образом, хотя учетные годовые ставки сделок совпадают, их процентные годовые ставки (доходности) различны.

Все расчеты с долговыми обязательствами, как процентными, так и дисконтными, осуществляются по основным формулам (2.5) (2.12) и (2.13) — (2.23). Зная, например, учетную ставку и учетную цену векселя, можно легко найти его номинал (сумму погашения).

Пример 2.13. Пусть вексель со сроком до погашения 4 мес. учтен в банке по цене .#1080. Каков номинал векселя, если учетная ставка банка 30\% годовых? Решени е. Учетная цена Р связана с номиналом ґ соотношением

P = Hl -dT).

Следовательно, получаем уравнение

1080 = F 1-0,3 —

)

относительно F, решая которое найдем

Хотя сделки с процентными и дисконтными бумагами были описаны как два различных класса сделок, между ними нет «непроходимой границы». Так, начатая как процентная, сделка может завершиться тесно связанной с ней дисконтной сделкой. Это имеет место, например, при учете процентных бумаг, операции, вполне аналогичной учету векселей. Поясним ее на примере.

Пусть инвестор покупает депозитный сертификат со сроком погашения 6 мес. по номиналу (F) в .'#1000 и с процентной ставкой / = 12\% годовых. Покупая сертификат, инвестор «открывает» процентную сделку. Начальная стоимость S0 сделки совпадает с номиналом, так как сертификат был куплен по номиналу

S=F= 1000(.-#).

Допустим, что через 4 мес. ему понадобились наличные, и он решает продать сертификат, т.е. закрыть сделку. Он может сделать это, продав сертификат банку (выпустившему сертификат или другому). Банк, естественно, купит или, как еще говорят, учтет сертификат не по его полной стоимости (сумме погашения), складывающейся из номинала и процентов за 6 мес, т.е.

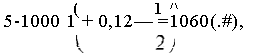аза меньшую сумму, т.е. с дисконтом. Обычно для подобных операций банк фиксирует нормированную, например годовую, учетную ставку сі. Если для нашего примера взять d = 24\%, то банк учтет (купит) сертификат по цене:

P = (l-dT)S = l~0,24 1060 = 0,96-1060=1017,6(.-tf).

Здесь Т— срок, оставшийся до погашения сертификата, т.е. 2 мес, или 1/6 года. Заметим, что этот срок не имеет ничего общего со сроком сделки инвестора, который составляет 4 мес (от покупки до учета). Таким образом, сданным сертификатом осуществляются две сделки.

9-5169

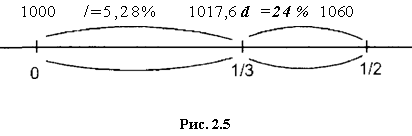
Одна, осуществляемая инвестором, состоит в покупке сертификата за 1000 и продаже его банку через 4 мес. за PJR 1017,6, и другая, осуществляемая банком, состоит в покупке сертификата по 1017,6 и погашении его через 2 мес. по полной стоимости S — ./'1060. При этом инвестор, получив за 4 мес, доход в .#17,6, реализует доходность

:_P-SQ _ 1017,6-1000

TSQ 1/31000

или 5,28\% годовых, что значительно меньше, чем «обещанная» доходность, представляемая процентной ставкой сертификата / — 12\%. Эту доходность инвестор мог бы реализовать, если бы держал сертификат до погашения.

С другой стороны, учет банком сертификата с дисконтом дает ему прибыль

10601017,6 =42,4(.#) за 2 мес, т.е. доходность

42 4

/= /' =0,25, 1/61017,6

или 25\% годовых, что намного больше обещанной ставки /0 = 12\% годовых. Это и естественно: прибыль банка означает убыток инвестора (при фиксированных параметрах сертификата).

Таким образом, учет долговых обязательств, т.е. покупка их банком до срока погашения, означает окончание сделки с этим обязательством для его владельца (инвестора, кредитора) и начало сделки для банка (или другого кредитного учреждения). Поэтому при расчете параметров сделок, связанных с долговыми ценными бумагами, необходимо проявлять осторожность и тщательно следить за «привязкой» реквизитов ценной бумаги к действительным параметрам анализируемой сделки. Для этой цели полезно строить временные диаграммы с указанием соответствующих событий. Так, для рассмотренного выше примера подобная диаграмма имеет вид, изображенный на рис. 2.5.

В приведенных выше примерах дисконтных сделок временные параметры задавались в месячной или непосредственно в модельной шкале Т. На практике они задаются в календарной шкале. Таким образом, для использования теоретических формул необходимо (см. примеры 2.7 и 2.8) выполнить предварительное преобразование временных параметров.

Пример 2.14. Вексель номиналом $1000 куплен по иене S850 за 90 дней до погашения. Найти соответствующие: а) учетную и б) процентную ставки сделки. Решение. Исходя из данных задачи без преобразований можем найти дисконт

D= 1000 850 = 150(5),

150 ПІЧ

w = = 0,15,

1000

а также за период сделки: а) учетную ставку

или и-= 15\%;

б) процентную ставку

, = 252 = 0.1765,

850

или г = 17,65\%.

Найти нормированные ставки без указания правил преобразования, описанных в §1.6, невозможно. Допустим, что выбрано правило АСТ/360. Тогда нормированная учетная ставка

rf = ^ = 0.15.^ = 0A

Т 90

или 60\%, а нормированная процентная ставка

/=-=0,1765-—= 0,7059, Т 90

или 70,59\%.

Приведенные примеры сделок с долговыми обязательствами должны убедить читателя в чрезвычайной важности точного учета используемых временных соглашений. Так, полученные в последнем примере значения нормированных учетной и процентной ставок зависят от конкретного правила измерения периодов времени в годовой шкале. Было выбрано банковское правило АСТ/360 — достаточно типичное для дисконтных инструментов денежного рынка, например, США. Однако в Великобритании расчет этого примера был бы осуществлен (если бы денежные суммы задавались в фунтах стерлингов) по правилу АСТ/365. К тому же даже в США банковское правило применялось бы прежде всего для расчета учетной ставки. Если бы инвестору понадобилось значение процентной ставки как меры доходности сделки с векселем, то он мог бы использовать правило, отличное от банковского, например АСТ/365 или ACT/ACT.

Хотя для данного типа долговых инструментов или сегмента рынка обычно используется одно из многочисленных временных правил, традиционно закрепленное за ними, может возникнуть необходимость расчета конкретной сделки и подругам временным правилам преобразования. Обычно это происходит при сравнении эффективности сделок с инструментами различных типов или сделок из различных сегментов финансового рынка. В таком случае применять разные схемы временных преобразований для разных сделок некорректно, поскольку временные характеристики сделок будут вычисляться по разным правилам. Уже отмечалось, что в разных странах используются разные схемы для вычисления длины временных промежутков в годовой шкале. Так, на денежном рынке США для Казначейских векселей США общепринято правило АСТ/360, тогда как для аналогичных Казначейских векселей Великобритании используется правило АСТ/365. При необходимости сравнения сделок на этих рынках необходимо выбрать какое-либо одно из этих (или, возможно, других) правил, чтобы временные характеристики сделок оценивались в одной шкале.

Таким образом, хотя логическая структура приведенных в этой главе формул, безусловно, не зависит от конкретных правил измерения временных промежутков, их конкретные значения определяются лишь относительно выбранных правил. В последнем примере для нормированной процентной ставки, те. доходности сделки с векселем за период до погашения, задаваемой единственной формулой

т{р Г

получим для данных F = $1000 и Р — $850 целую серию возможных значений /, определяемых конкретным правилом представления периода сделки, равного 90 дням в годовой шкале:

АСТ/360/ = 0,7059;

АСТ/365 -/ = 0,7157;

АСТ/365 (Япония) — / =0,7237, если период сделки високосный; ACT/ACT — / = 0,7157, если период лежит в пределах невисокосного года;

ACT/ACT — /=0,7176, если период лежит в пределах високосного года;

ACT/ACT — 0,7157 < і < 0,717'6, если часть периода приходится на високосный и часть на не високосный годы.

Как видно из §1.6, приведенный выше список далеко не исчерпывает всех возможных случаев.

Заметим, что выше цена Р была задана в долларах. Если бы речь шла, например, о сделке с Казначейскими векселями США, то цена векселя в таком случае могла бы задаваться косвенно, посредством котировки, которые для рынка Казначейских векселей США осуществляются в терминах учетной став/си с подразумеваемым применением банковского правила.

Так, дилер, оперирующий на этом рынке, мог выставить котировки трехмесячного Казначейского векселя (90 дней) 8,50\% на покупку и 8,48\% на продажу. Это означает, что дилер согласен купить вексель по цене

( 1А

7^=1000 1-0,0850-=978,75(5),

а продать по цене

(

Я =1000. 1-0,0848-==978,80(5).

пр ^ 4j

Разница между этими ценами составляет дилерский спред цен, т.е. доход, получаемый дилером с полной сделки (т.е. покупки с последующей продажей) с каждым векселем. Лицо, купившее вексель у дилера по цене Р = §978,80, при погашении через 3 мес. заработает $21,20.

Нормированную процентную ставку (доходность к погашению) такой сделки обычно находят, используя правило АСТ/365:

21 20

/=—^— = 0,0878, 978,80-Ц

или 8,78\% годовых.

Этот пример любопытен тем, что в нем используются два различных временных правила при расчете одной и той же сделки. Так, покупатель векселя у дилера сначала по котировке цены продажи (в терминах учетной ставки) найдет долларовую цену посредством банковского правила, а для оценки доходности сделки воспользуется правилом АСТ/365.

Заметим, что в этом случае нельзя (как это делалось в примере 2.8) применять формулу (2.16), связывающую учетную и процентную ставки, поскольку в этом случае возникает неопределенность со значением срока Т. Если этот срок задать в соответствии с банковским правилом, то вычисленная доходность к погашению будет соответствовать именно этому правилу, а не примененному выше правилу АСТ/365. Подстановка значения срока в соответствии с правилом АСТ/365 также некорректна, поскольку учетная ставка (котировка) подразумевает в соответствии с принятым на рынке Казначейских векселей применение банковского правила (АСТ/360).

На этом закончим предварительное обсуждение простых кредитных сделок и связанных с ними характеристик, прежде всего процентной и учетной ставок.

Вопросы и упражнения

Опишите математическую модель простой кредитной сделки. Какой вид имеет представляющий поток сделки, если проценты выплачиваются: а) в конце периода сделки? б) в начале периода сделки?

Дайте содержательную трактовку простой нормированной процентной ставки сделки. Какую роль играет эта ставка на краткосрочном кредитном рынке?

Как связаны между собой учетные и процентные (за период и нормированные) ставки?

Что такое простой класс сделок? ракова связь между простыми процентными и простыми дисконтными классами сделок?

Укажите основные временные и финансовые параметры, определяющие вексель и депозитный сертификат,

Что такое стандартная сделка с долговым обязательством?

Как связана цена долгового обязательства и рыночная процентная ставка?

Как определяется доходность к погашению долгового обязательства? Как связана эта доходность с рыночной процентной ставкой?

Задачи

Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 30 дней составляет 45\%; при сроке 60 дней —48\%; при сроке 90 дней — 50\%. Рассчитайте доход клиента при вкладе .К* 100 тыс. на указанные сроки. Год невисокосный, правило банковское.

Коммерческий банк привлекает средства под простые проценты с процентной ставкой 36\% годовых, Клиент внес Mb млн на депозит с 12 февраля по 24 апреля. Определите величину коэффициента роста и наращенную сумму для временных правил: а) АСТ/365; б) банковского; в) приближенного — 30/360. Год невисокосный.

Клиент получил в банке кредит сроком на 3 мес. Mb мли. Сумма возврата кредита равна 'ЖЪ млн. Определите процентную ставку банка.

4. Фирме необходим кредит в .^50 млн. Банк согласен выдать кредит, если

возвращенная сумма долга будет равна М 60 млн. Учетная ставка составляет 210\%

годовых. На какой срок выдан кредит?

А занимает у В под 15\% годовых сроком на 9 мес. и выписывает на В вексель на J?Q0 000. Через 3 мес. В продает вексель С, который желает обеспечить себе доходность при погашении 18\% годовых. Какова цена векселя при продаже? Сколько заработал В! Какова соответствующая учетная ставка сделки за период и годовая0

Вексель со сроком погашения через 5 мес. на сумму S1500 учитывается в банке за 2 мес. до погашения по учетной ставке 15\% в месяц. По какой цене будет учтен вексель? Каков доход банка? Каков доход векселедержателя, если цена эмиссии векселя (т.е. основная сумма долга) равна S1000?

Инвестор приобрел депозитный сертификат с номиналом .^500 000 и процентной ставкой 70\% годовых. Срок погашения сертификата 9 мес. Через 5 мес. инвестор продал сертификат. К этому моменту ставка поднялась до 80\% годовых. Сколько заработал инвестор? Какую прибыль при погашении получит новый владелец сертификата?