3.3. приведение денежных сумм в схеме простых процентов

3.3. приведение денежных сумм в схеме простых процентов

В предыдущем параграфе мы изучали динамику процесса накопления с фиксированной нормированной процентной ставкой. Процесс процентного накопления является детерминированным процессом в том смысле, что задание начального состояния полностью определяет будущее поведение процесса (см. § 1.4). Эта детерминированность позволила определить понятие будущего или накопленного к моменту t значения денежной суммы SQ, относящейся к моменту t0. Данное значение определяется соотношением

^ = /^(50) = 50(1+/(г-/0)), t>tQ. (3.13)

В финансовой литературе говорят также о будущей, или накопленной, стоимости суммы S0. Оператор будущей стоимости FV позволяет найти приведенное к будущему моменту / значение любой суммы S.r относящейся к моменту t(j или, как еще говорят, привести (преобразовать) эту сумму к моменту t. Задавая такое преобразование, которое определяется исключительно значением ставки /, мы приходим к более общей точке зрения, чем при изучении динамики индивидуального процесса процентного накопления.

По существу, мы переходим к рассмотрению семейства (класса) всех таких процессов с общей ставкой накопления /. Формулу (3.13) при таком обобщенном подходе рассматриваем просто как закон преобразования событий или денежных сумм. Традиционно момент (будущий), к которому приводятся (преобразуются, переносятся) денежные суммы, называется одним из следующих терминов: моментом приведения, полюсом, фокальной датой, моментом валоризации (см. § 5). Валоризация означает оценивание, т.е. нахождение стоимости в заданный момент времени.

Отметим, что процесс приведения полностью определяется коэффициентом роста

10-5169

a(t0, t)=+l(t-tQ), который задает динамику накопления в схеме простых процентов.

Заметим, что процесс процентного накопления однозначно определен не только в смысле будущих состояний по заданному начальному состоянию, но имеется некоторая определенность относительно прошлого. Более точно, текущее состояние (t, Ss) однозначно определяет начальный капитал S , если известен начальный момент / процесса. Конечно, предполагается известным также и основной параметр — нормированная ставка / (ставка накопления). Это немедленно следует из однозначной разрешимости уравнения динамики

S, = S0(+i(t-t0)) относительно SQ: _

i+/(/-/0)

Определение S0 по заданному состоянию (/, St) является задачей, обратной той, что решалась в предыдущем параграфе. Ее содержательный смысл формулируется так: какую сумму следует инвестировать в момент /0 по ставке /', чтобы к моменту / накопить сумму

Сумма дУ называется текущей (дисконтированной, сегодняшней, настоящей, приведенной) стоимостью суммы Sty а оператор DVt приведения St к моменту времени tQ — оператором текущей стоимости:

Если t{) — О, то формула (3.14) примет вид

1 + //

Операция приведения к начальному моменту суммы Sf называется дисконтированием этой суммы. Иными словами, данная операция является обратной по отношению к рассмотренной выше операции нахождения будущей или накопленной суммы.

Заметим, что текущее значение в момент tQ события или суммы С{ в финансовой литературе обычно обозначают PV (С,). Однако в последнее время это обозначение используется в более общей ситуации как обозначение текущей стоимости суммы (события) в любой (не обязательно прошлый) момент времени (см. определение оператора PV ниже). Поэтому в тех случаях, когда необходимо подчеркнуть, что речь идет именно о прошлых (по отношению к данному событию) момен-

3.3. Приведение денежных сумм в схеме простых процентов 147

тах, используется обозначение DVT(С,). Обозначение DV— сокращение от англ. Discount Value. Коэффициент

*('лК ./! (ЗЛ6)

l + /(f-/0) 1 + *Г

где Т — t — t называется коэффициентом дисконтирования в схеме простых процентов. С его помощью оператор дисконтирования запишется в виде

DVlt(S,) = S,d(t,t,). (3.17)

Как и коэффициент роста, коэффициент дисконтирования зависит только от разности Т = t — /0, а не от моментов времени /0 и / непосредственно. Это дает основание для введения одномерного или стандартного коэффициента дисконтирования

dT ~—-— Т 1 + /Т

так, что

d(t,t(i) = dT DVta(S,) = StdT.

В случае г0 = 0 выражение для коэффициента дисконтирования упрощается:

В этом случае оператор дисконтирования запишется в виде

DVa(S,) = S,dr

Обратная задача решается не только для модели накопительного счета, но и в других ситуациях. Так, предприятие, нуждающееся в дополнительных оборотных средствах, зная выручку, которую оно получит в результате реализации продукции в течение некоторого периода, может определить максимальный объем займа, который оно в состоянии себе позволить при условии своевременного покрытия долга.

Пример 3.5. Какую сумму необходимо вложить в настоящий момент /0 сроком на 2 года под 5\% годовых, чтобы накопить />П0ОО?

Решение. Положим для простоты /() = 0. Так как в данном случае S2 — .#1000 и / = 0,05, то

1000 = шоо

0 1 + 2-0,05 1,1 ;

Итак, семейство процессов роста с одной и той же ставкой порождает соответствующие операции преобразования (или приведения)

^ V,

<zcT Л(к финансовых событий как к

будущим, так и прошлым мо-

х ментам времени. При этом

переход к будущим моментам

Рис З 3

задается правилом

К = Л;(С,) = С,й(/,т) = С,(1+,-(т -/)), т>1,

а переход к прошлым моментам — правилом

Оба оператора можно объединить в рамках одного общего оператора приведения, называемого оператором текущей стоимости РУг, который для любого события (/, С) определяется формулой

/ ч [^г(сЛ = С/йМ> если г > г; rV " [ХЖДС,) = С,</(ґ,т), еслит</.

Операция приведения событий к моменту времени т наглядно изображается на рис. 3.3.

Пример 3.6. Пусть в некоторой временнбй шкале сумма S{ = .-*?200 относится к моменту f = 1, а сумма 5 = .-#600 к моменту t7 = 3. Найти приведенные к моменту т = 2 значения этих сумм, если нормированная процентная ставка / = 20\%.

Решени е. Поскольку (х < г, то приведенное к т значение Sl = .-#200 есть будущая стоимость этой суммы, т.е.

^ = FV2 ) = 200(1 + 0,2) 240 (. #).

Далее, так как t > г, то приведенное к гзначение S2 = .#600 — текущая (дисконтированная) стоимость этой суммы, т.е.

2 п 2> 1 + 0,2 v '

Введенному выше общему оператору приведения (текущей стоимости) РУг в схеме простых процентов соответствует обобщенный коэффициент приведения или обобщенный коэффициент дисконтирования:

а(г,т) прит>г;

[d(t,r) прит<г. Из очевидного соотношения

тЦт,г) = 1

следует свойство самосопряженности коэффициента v(t, т) {см. §1.5):

и(г,т)

1

(3.J8)

V

Поскольку коэффициент v(/, т), как и коэффициенты a{t, т) nd(t, г), зависит только от разности Т= тt, то можно ввести (упрощенный) одномерный коэффициент приведения

а(Т)= + іТ, еслиГ>0;

■г=о(7>

d(-T)~——, еслиГ<0.

1-/Т

(зл9)

Свойство (3.18) для коэффициента v(T) перепишется в виде

1

(-ту

о(7>.

и

С помощью обобщенных коэффициентов дисконтирования оператор текущей стоимости представляется в виде

Vx = PVx{C,) = C,v{l,x) = C,vT.

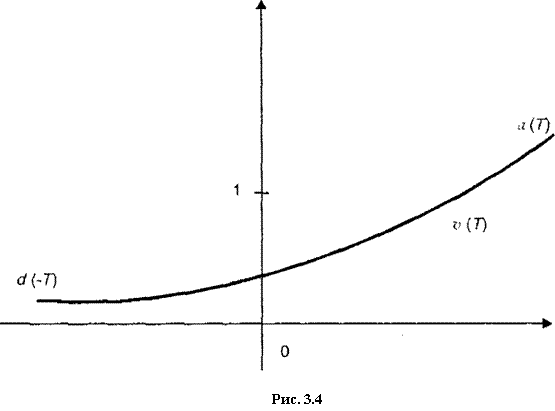График функции v(T) изображен на рис. 3.4.

м

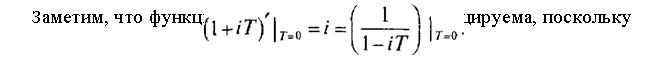График функции v(T), таким образом, «гладко склеен» из луча — графика функции роста а( Т) и графика функции d{—T).