8.4. номинальная и эффективная нормированные ставки

8.4. номинальная и эффективная нормированные ставки

Номинальные ставки. Выше были приведены основные модели накопительного счета (вклада) в схеме сложных процентов. Основной параметр таких моделей — ставка начисления, описываемая в заданной временнбй шкале парой (А, /'), состоящей из периода начисления h и числового значения / ставки.

На практике в случае накопительных счетов, как и для кредитных сделок, часто используют не ставки начисления, а так называемые номинальные ставки, относящиеся к некоторым, заранее выбранным периодам. Период, к которому относится номинальная ставка, называется номинальным. Он непосредственно не связан с периодом начисления и может выбираться произвольно.

Цель введения номинального периода состоит в осуществлении единообразного способа задания ставок, определяющих динамику накопительных счетов. Кроме того, номинальный период играет роль периода приведения, к которому приводятся значения ставок начисления. Это позволяет сравнивать такие ставки. Хотя номинальный период может быть выбран произвольно, на практике он выбирается естественным образом, связанным с используемой временной шкалой. Чаще всего номинальный период'представляет собой просто единичный (базовый) период временной шкалы. Так, если шкала годовая, то номинальный период равен году и все номинальные ставки — годовые. Приведение ставок начисления к единичному периоду временной шкалы принято называть нормированием, а соответствующее значение ставки — нормированным.

Таким образом, нормированные номинальные ставки в накопительных схемах сложных процентов вполне аналогичны нормированным ставкам простых кредитных сделок и нормированным ставкам начисления в схеме простых процентов. Во всех случаях идея состоит в приведении (нормировании) ставок, непосредственно связанных с различными периодами, к некоторым стандартным (например, базовым), периодам.

Поскольку роль номинальной ставки — стандартизированное представление ставок начисления, то ее задание предполагает, кроме указания номинального периода и значения самой ставки, задание дополнительной информации, позволяющей легко определить соответствующий период начисления, а также правило для вычисления значения ставки начисления.

В качестве дополнительной информации, устанавливающей связь между номинальной ставкой и ставкой начисления, используют либо непосредственно период начисления, либо так называемую кратность начисления. Кратность начисления равна отношению номинального периода к периоду начисления. Она, таким образом, показывает число раз. которое период начисления содержится в номинальном периоде.

Иногда понятие номинальной ставки вводят несколько иначе, основываясь на так называемой кратной выплате процентов. Этот подход можно пояснить следующим образом.

В соответствии с моделью накопительного счета проценты за период начисления присоединяются к сумме счета в конце периода начисления. Это лишь один из способов так называемой актуализации, т.е. преобразования интервальной величины, какой являются проценты за период, в мгновенную величину (см. гл. 1). Имеется бесконечное число способов такого преобразования или, применительно к нашему случаю, выплаты процентов: в начале, середине периода и т.п. Здесь нас будет интересовать один весьма распространенный способ, при котором проценты за период начисления «выплачиваются» несколько раз одинаковыми суммами. Глагол «выплачиваются» взят в кавычки, поскольку в накопительных моделях проценты не выплачиваются, а присоединяются к счету, т.е. сумма счета увеличивается. Эту операцию мы назвали начислением. Термин «выплачиваются» понадобился для того, чтобы избежать коллизии понятий исходного начисления один раз в конце (исходного) периода начисления и нового (многократного) начисления в течение этого периода.

Примерами такой схемы могут служить выплаты начисленных за год процентов дважды в конце каждого полугодия, четырежды в конце каждого квартала или 12 раз в конце каждого месяца. Легко понять, что при таком подходе исходный период начисления перестает быть фактическим периодом начисления; фактическими периодами начисления становятся подпериоды, составляющие исходный период, поскольку в конце именно этих подпериодов осуществляется фактическое начисление, т.е. присоединение соответствующих этим подпери-одам долей общей суммы начисленных за исходный период процентов.

В общем виде упомянутую выше схему можно представить следующим образом. Исходный период начисления h разбивается на т одинаковых подпериодов, и сумма процентов за этот период выплачивается т раз в конце каждого подпериода. Величина каждой выплаты равна

т

(8.23)

так, что общая сумма выплаченных за исходный период начисления процентов будет той же — Jh. Поскольку исходный период h фактически не является периодом начисления, назовем его номинальным периодом и обозначим Ь. Действительным периодом начисления будет период Ь/т; именно его обозначим теперь через И:

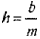
(8.24)

Целое число т, т.е. число фактических начислений за исходный номинальный период, назовем кратностью начисления.

Переход к другому, более мелкому периоду начисления означает фактически изменение и ставки начисления. Если для исходного (номинального) периода Ъ соответствующая ставка будет равна /4, то из равенства (8.23) следует, что

'W*/^-(8.25) т

Иными словами, ставка за фактический период начисления в т раз меньше ставки за номинальный период.

Хотя описанный подход может служить мотивацией для введения номинальных ставок, он не является вполне строгим, так как начисление по ставке ih не будет давать одинаковых процентных сумм

J h/m ' т

для всех подпериодов исходного номинального периода. На самом деле в основе этого подхода заложено выполнение равенства (8.25), а не (8.23).

Задание номинального периода и периода начисления осуществляется в некоторой временной шкале, единичный период которой может как совпадать, так и не совпадать с упомянутыми периодами. На практике наиболее часто используют номинальный период, совпадающий с единичным периодом временнбй шкалы. В дальнейшем будем рассматривать именно этот случай. Тем не менее начнем с общего определения номинальной ставки.

Формально номинальная ставка в заданной временной шкале Т задается тройкой (/>, Л,у), где Ь — длина (номинального) периода; h — длина периода начисления;,/ — числовое значение номинальной ставки.

Другой способ задания номинальной ставки состоит в задании тройки (Ь, т, у), где b и j имеют тот же смысл, что и выше, а т — кратность начисления, т.е.

тЛ. (8.26)

Заметим, что длины b и И выражены в единицах временнбй шкалы!.

Задание номинальной ставки подразумевает ее связь со ставкой начисления, описываемую соотношением

Пример 8.4. Пусть в годовой шкале номинальная ставка имеет вид 1 -, — ,12\%

1,2 12 ) Найти кратность и ставку начисления.

Решение. Согласно определению номинальной ставки как тройки (Ь, Л, у),

вданном случае (в годовой шкале) имеем: номинальный период b — полугодие, т.е.

b — 1/2; период начисления Л — месяц, т.е. h = 1/12; величина номинальной ставки j —

12\% за полугодие. Таким образом, за этот период проценты начисляются

т~—— =6 1/12

раз, те, кратность начисления — 6 раз за полугодие, а ставка начисления itJn = — = 2, т.е. 2\% в месяц.

Пример 8.4 несколько искусственный. Как уже было сказано, на практике номинальный период совпадает с единичным промежутком временной шкалы. Обычно в качестве такого периода берется год. Тогда говорят о номинальной годовой ставке, подразумевая явное указание либо периода, либо кратности начисления. В случае, когда номинальный и единичный периоды временной шкалы совпадают, тройка, представляющая номинальную ставку, имеет вид (1, h.j) или (1, /и,у), где h — период начисления, выраженный в единицах временной шкалы; т — кратность начисления. При этом

и 1 1 /? = —; т-~

т И

и данная номинальная ставка, согласно сказанному, будет являться нормированной.

Фактически задание номинальной ставки сводится к заданию периода начисления и ставки j (т.е. просто пары (А, У)) или кратности начисления т и значения ставки (т.е. пары (от, /)). Однако не будем использовать обозначения номинальной ставки как пары:

во-первых, потому, что в формулах прежде всего нужно лишь значение уставки;

во-вторых, использование пары (А, У) может привести к смешению номинальной ставки со ставкой начисления, которая также задается двумя элементами: периодом начисления и значением ставки.

Чтобы не путать виды ставок, будем использовать специальные индексные обозначения. Номинальную ставку с периодом начисления h мы обозначим как /(/ , а ее значение с указанием кратности начисления т — в виде i(m Однако в дальнейшем мы также будем иногда использовать обозначение У для указания значения именно номинальной ставки. С другой стороны, обозначение / (без индексов!) будет всегда означать нормированную ставку начисления, т.е. ставку с единичным периодом начисления. В любом случае в определении номинальной ставки должно явно или неявно содержаться указание на период или кратность начисления. Говорят, например, о 10\%-ной годовой ставке, начисляемой дважды в год, или, что то же самое, о 10\%-ной годовой ставке с начислением по полугодиям.

Использование скобок позволяет отличать номинальную ставку от ставки начисления, которую обозначаем как /Л.

Итак, нормированная номинальная ставка, относящаяся к единичному периоду временнбй шкалы, задается двояко:

указанием самого периода начисления А, выраженного в единицах базового периода; тогда ставка начисления определяется как

к=\^ <8-27>

указанием кратности начисления т за базовый период; в этом случае период начисления определяется по формуле

1 (8.28)

й = ' т

а ставка начисления

<>—. (8.29)

т

Если h = 1 и, значит, т = 1, то период начисления совпадает с единичным периодом временнбй шкалы. В этом случае номинальная нормированная ставка превращается в нормированную ставку начисления:

/ = /О) = /

(I) г

В этом случае мы пишем просто /.

Поскольку ставка начисления /А непосредственно выражается через номинальную ставку /' ~ i{m числовое значение которой здесь обозначим как у, то можно переписать уравнения динамики накопительного счета в терминах номинальной ставки, подставляя выражения для ставки начисления

w mm

в уравнения (8.8) и (8.9). Тогда для моментов начисления tn — tQ + nh получим

S,, = S„(l-iJ=(+hjy = S,„[l+£j , (8.30)

и поскольку t -t

то имеем

S, =S, (+hj) * =5, 1+— . (8.32)

Заметим, что выражение

Ґ j Vй

есть не что иное, как множитель наращения или коэффициент роста за единичный (базовый) период времени при т-кратном начислении по номинальной ставке], соответствующей ставке начисления /. Следовательно,

^=v«*=(°w Г<8-33>

Индекс п в вышеприведенных формулах обычно опускают и пишут просто S^Sjl+hjf-'^^S^l+^J , t = t0+nh, /ieN, (8.34)

т.е. момент / должен быть в этом случае моментом начисления и промежуток t — ro должен содержать целое число

периодов начисления. Напомним, что в формулах (8.30), (8.32) — (8.34) j обозначает номинальную ставку.

Г1 р и м е р 8.5. Найти накопленное значение суммы .'#300 за 4 года, если номинальная годовая ставка:

а) 10\%, период начисления — 6 мес;

б) 8\%, период начисления — в 2 года.

Решение.

/і = 1; т = 2; іт=і{1) = Ю\%

а) Для годовой шкапы при /() = 0 и / = 4 имеем

I 2

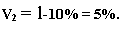п = tm = 4-2 = 8. S. = 300<l+0,05)s 443,24(..#).

и ставка начисления за 6 мес.

Число полугодий составляет Следовательно,

б) В данном случае

Л = 2; т-п-— = — = 2

г л 2

и двухгодичная ставка начисления

/, = Шт = 2-8\% = 16\%.

Следовательно,

Si 300(1+0,1 б)2 = 403,68(.#).

Важно понимать, что нормированная номинальная процентная ставка относится к единичному (базовому) промежутку временной шкалы. На практике это обычно годовая ставка, тогда как ставка начисления — это ставка за период начисления.

Полученные выражения для динамики накопительного счета, записываемые в терминах номинальных ставок / и і(т) в виде

1

V

т }

справедливы без оговорок лишь для моментов начисления t= tQ + nh, т.е. для промежутков [f0, t), содержащих целое число периодов начисления h.

В § 8.3 мы сформулировали три обобщения (интерполяции) уравнения динамики накопительного счета, выраженного через ставку начисления. Подставляя в эти обобщенные уравнения (8.20) (8.22) выражение для ставки начисления через номинальную ставку, получим соответствующие формулы, отражающие динамику накопительного счета, в терминах номинальных ставок. Так, при tQ = 0 получим для моделей следующие формулы:

— кусочно-постоянная:

( -и \[т']

1+

т )

/>0;

(8.35)

непрерывная:

( ,-Н 1 +

т )

/>0;

(8.36)

— смешанная:

т )

1

т )

t>0.

(8.37)

Как уже упоминалось, мы будем работать исключительно с непрерывной моделью. В дальнейшем ограничимся формулировкой результатов для этой модели в терминах номинальной ставки лишь для ставки ilm) с /я-кратным начислением, имея при этом в виду, что запись аналогичных формул в терминах номинальной ставки / получается тривиальной заменой і(т) на / и /т на п.

Для непрерывной модели для произвольного начального момента времени Г0 > 0 из (8.9) получаем очевидное обобщение формулы (8.35):

т

S=S.

1 +

т J

(8.35')

Прежде чем перейти к изучению непрерывной модели, напомним еще раз, что номинальная ставка является просто нормированным представлением ставки начисления, т.е. приведением ее к единичному периоду временной шкалы и, следовательно, ее удобно использовать, когда рассматривается не одна, а несколько или много ставок начисления.

Непрерывное начисление и бесконечно-кратные номинальные ставки. Явное разделение номинальной величины ставки с выделением ее числового значения и кратности (частоты) начисления позволяет раздельно исследовать эффект этих факторов для данного инвестиционного периода. В самом деле, рассмотрим период, состоящий из п базовых промежутков, например при / = 0 и / = п. Тогда для семейства номинальных ставок i{m) с различной кратностью начисления, но с общим значением i(m) =j накопленная сумма за п периодов для начальной суммы согласно (8.34), может быть представлена в виде

S' — Sn

(

т

Ґ ; У"

т )

1 +

]_ т )

Из математического анализа известно, что при т > т

1 +

<

1 +

V

т

т.

или в терминах множителей наращения

а

т.е. большей частоте начисления соответствует больший множитель аШ) и тем самым — большая сумма накопления.

Далее заметим, что поскольку период начисления, соответствующий номинальной ставке /"",, равен h = /т, то при т —> °° получаем, очевидно, h —> 0. Поэтому в предельном случае при т —> °о приходим к непрерывному начислению процентов. При этом для коэффициента роста получаем предельные значения

= еу. (8.38)

lim

1 +

V т)

Следовательно, при непрерывном начислении процентов по номинальной ставке j накопленная за п периодов сумма

5>V. (8.39)

Отметим, что во всех приведенных выше формулах числа тип предполагались, вообще говоря, целыми неотрицательными числами. Ниже рассмотрим обобщения этих формул, однако уже здесь можно отметить особенность формулы (8.39). При непрерывном начислении естественным образом исчезает проблема соизмеримости периода начисления и базового периода. Поэтому при непрерывном начислении (8.39) можно использовать для любых периодов. Так, для периода длины Г накопленная сумма будет выражаться формулой

ST=S0&rt (8.40)

а соответствующий коэффициент роста примет вид

a{f]=eJT. (8.41)

Конечно, на практике непрерывное или бесконечно-кратное начисление непосредственно реализовать нельзя, но оно легко реализуется схемой накопления, задаваемой формулой (8.40), означающей, что инвестору, открывшему счет на сумму S0 в момент времени tQ = 0, в любой момент времени t приписывается (начисляется) сумма 5,

определяемая выражением р й

Sj — S(ie . (о.42)

При этом проценты, начисленные инвестору за период [0, /|, составят

I([0,t]) = S,-St = S,{^-).

О бесконечно-кратном или непрерывном начислении будет более подробно сказано ниже, а сейчас вернемся к дискретным схемам начисления (с конечной кратностью).

Эффективные ставки. Каждая дискретная схема начисления определяется либо ставкой начисления ih с периодом начисления И, либо нормированным представлением этой ставки, т.е. номинальной ставкой /(лт), где т = 1/Vi — кратность начисления номинальной ставки. При этом т

Динамика роста в этом случае (для непрерывной модели) выражается равенствами (при f = 0)

(

1 +

V

ш )

Напомним, что величина

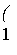
1 +

МЛ

=(ih)"

где /А — ставка начисления, соответствующая периоду начисления А=1/т, представляет собой коэффициент роста инвестированной суммы 50 за единичный период по ставке начисления /, соответствующей номинальной ставке fm) с m-кратным начислением:

^0

Но тогда

будет процентной ставкой за единичный (базовый) период временной шкалы. Эта ставка называется нормированной эффективной ставкой (за единичный период), соответствующей ставкам начисления ih и номинальной i(m). Заметим, что эффективная ставка является, как и номинальная, еще одним нормированным (т.е. приведенным к единичному периоду) представлением ставки начисления /А. Эффективная ставка является значением отображений

1

или

(

•И

V

т )

Эффективную нормированную ставку, соответствующую ставкам начисления ih и номинальной i(m будем обозначать как , , или

'зф, если понятно, какой период начисления рассматривается, либо, наконец, просто /, если h = I. Таким образом,

со

г , г і{т) ^

1. (8.43)

Отметим еще особый случай, когда/г = /?г = 1, т.е. период начисления совпадает с единичным периодом временнбй шкалы. Тогда все три типа ставок совпадают:

1 эф

и можно говорить просто о нормированной ставке, которая воплощает все три типа ставок, и не использогіать в обозначении никаких дополнительных индексов, символов и меток.

Пример 8.6. Найти годовую эффективную ставку, соответствующую 10\%-ной годовой номинальной ставке, начисляемой дважды в год. Ре ш е н и е. В данном случае іа) = 10\%. Тогда

/^=^1+Mj -1 = (1,05)2 -1 = 0,1025, или 10,25\%.

Мы привели определение нормированной эффективной ставки, т.е. ставки за единичный (базовый) период, соответствующей номинальной ставке i{m) или ставке начисления /Л с h = 1/т. Заметим теперь, что если рассмотреть семейство номинальных ставок /(т) с различной кратностью начисления, но с общим значением i{m) — j, то получим соответствующее семейство эффективных ставок /У , причем

Am)

'эф

( iT

І+— -1. (8.44) V m J

Положим

lim/H =/H

Из (8.44) следует, что этот предел

&'=e'-l (8.45)

определяет эффективную ставку, соответствующую бесконечно-кратной (непрерывно начисляемой) номинальной ставке / Заметим, что период начисления h ~ /т, соответствующий номинальной ставке /("!>, стремится к нулю при т —> °°. Таким образом, со ставкой j — iieo) не связан никакой период начисления. Ставки у и /у связаны непосредственно лишь с единичным периодом временнбй шкалы, к которому они относятся.

Пример 8.7. Пусть j = 10\% есть номинальная головая ставка, начисляемая непрерывно. Какова соответствующая (нормированная) эффективная годовая ставка? Р е ш е н и е. При данных условиях

/Н^е0-1-1=0,1052,

т.е. /!;'= 10,52\%.

Знание эффективной (нормированной) ставки позволяет переписать выражение для накопленных сумм в виде

$. = ■5.0+ '*)"• (8-46>

Эта формула имеет совершенно естественный смысл. Поскольку

коэффициент f v„

есть коэффициент роста за единичный (базовый) период, то коэффициент (1 + / )" есть коэффициент роста за п единичных (базовых) периодов. Это соответствует общей логике сложных процентов. Иными словами, возвращаемся к простейшей формуле (8.2) с той лишь разницей, что теперь в качестве ставки начисления / берется эффективная ставка за период. Конечно, если h — т1, т.е. период начисления и базовый период совпадают, то также совпадают номинальная и эффективная ставки за периоды. В общем же случае можно применить простейшую формулу (8.2), вычислив предварительно эффективную ставку / по заданным параметрам номинальной ставки.

Номинальная и эффективная ставки для произвольных периодов начисления. В предыдущем параграфе выполнен переход от дискретной модели накопительного счета, определяемой периодом начисления И и ставкой начисления / за этот период, к непрерывной модели, описываемой уравнением (при to ~ 0)

J,-J.(l + i»r. '20.

Выражая нормированный коэффициент роста (1 + /А),/А за единичный период через эффективную нормированную ставку:

(1+'аГ=1 + 'эф»

20-5169

данное уравнение запишем в виде

(8-47)

Строго говоря, такое определение эффективной ставки в данном случае не вполне обоснованно, так как ранее оно было дано лишь для случая целочисленной кратности начисления за единичный период временной шкалы, т.е. когда т = l/h — целое число.

Сформулируем общее определение (нормированных) номинальной и эффективной ставок в непрерывной модели для любого периода начисления, выраженного в единицах временнбй шкалы.

Определение 8,1. Пусть Т — временная шкала; h — период начисления, выраженный в единицах временной шкалы; ih — ставка начисления. Тогда ставка

называется нормированной номинальной, а ставка

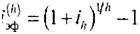
(8.49)

— нормированной эффективной ставкой, соответствующими ставке начисления /А. При этом номинальная и эффективная ставки, связанные равенством

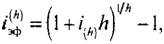(8.50)

также называются соответствующими друг другу.

Заметим, что по этому определению число т ~ jh может быть нецелым. Однако и в этом случае будем называть эту величину, обратную периоду начисления, кратностью (частотой) начисления и по-прежнему будем формулировать результаты в терминах номинальной ставки iim) = i{l/fl).

Определения (8.49) и (8.50) являются, естественно, применением введенной выше непрерывной модели накопления с динамикой, задаваемой уравнением

$=.У0(1 + /А)'

к единичному промежутку t — 1.

Рассматривая теперь семейство номинальных ставок i(l/h) с различными периодами начисления Л, но с общим значением, равным у", получим соответствующее семейство эффективных ставок

/О/л

'эф

где соответствующий множитель наращения аа/к) имеет вид

am=(+jhf. Логарифмируя и переходя к пределу, получим

\m { + jhf = j.

Отсюда, полагая

а—1.0

и

'эф ■

получаем, что

а = еЛ

и, следовательно,

эф

Таким образом, получили, что и в этом общем случае для непрерывной модели при непрерывном начислении процентов для нормированных коэффициентов роста и эффективной ставки имеют место те же самые предельные формулы (8.38) и (8.45), что и в случае кратного начисления процентов, и, следовательно, динамика накопления будет определяться той же самой формулой (8.42).

Пример 8.8. Пусть в годовой шкале задана ставка /, = 20\% с двухгодичным периодом начисления h = 2. Найти годовые номинальную и эффективную ставки, соответствующие этой ставке.

Решение. В данном случае т — і/2. Тогда номинальная годовая ставка

Ш_: _ /2 _ 20\% _

$ =(! + /• )1/2 -1 = 0,0954, или 9,54\%.

а эффективная годовая

'(2)

Хотя номинальная и эффективная ставки являются нормированными представлениями ставки начисления, их финансовые интерпретации существенно различны. Так, номинальная нормированная ставка не является фактической ставкой за номинальный базовый период (период приведения), тогда как эффективная нормированная ставка представляет собой фактическую ставку за период приведения в непрерывной модели накопительного счета. Говоря о том, что эффективная ставка — это фактическая ставка за период приведения, мы имеем в виду, что коэффициент роста счета за этот период в точности равен 1 + /' .

Подведем итоги анализа основной непрерывной модели накопительного счета в схеме сложных процентов. Сформулируем их в общем случае, когда в качестве начального момента рассматривается произвольный момент времени г0, а начальная сумма счета равна 5" Заметим, что распространение результатов для / = 0 на случай / Ф 0 вполне очевидно и не нуждается в дополнительном обосновании.

Непрерывная модель процентного роста задается одним из следующих четырех видов процентных ставок:

ставкой начисления і за период начисления h; соответствующая динамика описывается равенством

/>/0; (8.52)

5,=5„(1 + 0<m,v*, 'Sr0; (8.51)

нормированной номинальной ставкой iim) с кратностью начисления т с динамикой

st = s, 1+—

Ч т )

непрерывной (бесконечно-кратной) номинальной ставкой j — /(ве) с динамикой

St = Stcj{t4(>K t>t0; (8.53)

нормированной эффективной ставкой і с динамикой

S, =5(<(1 + /)'-'", tit,. (8.54)

Заметим, что способ задания модели с помощью нормированной эффективной ставки является на самом деле частным случаем задания с помощью ставки начисления /д, если период начисления совпадает с базовым (единичным) периодом времени. Как отмечалось выше, индекс в обозначении /, часто опускается и пишут просто /. Мы указали этот случай отдельно, так как для него закон динамики имеет наиболее простой вид, именно поэтому он часто используется в теории финансов.

С помощью нормированного коэффициента роста динамику накопительного счета в каждом из этих случаев можно записать в унифицированном виде

S^St/' (8.55) где а — нормированный коэффициент роста в модели, при этом:

— для модели с заданной ставкой начисления і.

«=0+4)"";

— для модели, задаваемой номинальной ставкой с /и-кратным начислением,

И,

а

1

V

т )

— для модели с непрерывным (бесконечно-кратным) начислением

а — qj.

Кроме того, отметим, что в каждой из этих моделей нормированный коэффициент роста связан с соответствующей эффективной нормированной ставкой основным соотношением

а = ] + і

эф'

(8.56)

Пример 8.9. Пусть в годовой шкале заданы ставки /', = 72,8\%, ііМ = 40\% и j = /("* = = 20\%. Найти соответствующие этим ставкам нормированные коэффициенты роста в непрерывной модели накопительного счета и будущую (накопленную) стоимость

Р е ш е н и е.

а) Для /, = 72,8\%, h 3 года и коэффициент роста имеет вид

а = (1 +ізу» = (1,728)^ = 1,2

и, следовательно,

S,=af=(l2)'.

б) Для/(4' = 40\%, А = 4,да = 4

а

^1+у) =f 1+— I =1,4641

и, следовательно,

в) Для j = /^ = 20\% и, следовательно,

S,=a' = (1,4641)'.

а = eJ = еп-2

В тех случаях, когда выбор конкретного вида ставки безразличен, будем говорить просто о ставке накопления, подразумевая под этим любую из четырех упомянутых выше. Выписанные уравнения динамики позволяют легко находить соотношения между различными видами ставок. Они определяются условием тождественности результата накопления для любого момента времени. Более подробно этот вопрос будет рассмотрен ниже в параграфе, посвященном эквивалентности процентных ставок.