8.5. учетные ставки в схеме сложных процентов

8.5. учетные ставки в схеме сложных процентов

Выше мы определили модель накопительного счета в терминах процентных ставок. Однако в гл. 2 было введено понятие учетной ставки w за период и нормированной учетной ставки а1. Попытаемся разобраться, как это понятие применимо к схеме сложных процентов.

Хотя построение модели накопления выглядит более естественным при использовании процентной ставки, тем не менее ее также легко выразить в терминах учетной ставки. Схема описания учетной модели накопления полностью идентична процентной схеме.

Выберем период временной шкалы, которую назовем учетным периодом. Его длину в выбранной временной шкале обозначим через И. Учетную ставку за этот период обозначим через dh. Разобьем временною шкалу на периоды длины h кратными точками: tn = t0 + nh, п = 0,1, 2, ... . Тогда состояния счета в концах k-vo учетного периода будут связаны соотношением

Sk_^Sk(l-dh), * = 1,2,...,л. (8.57) Отсюда немедленно следует соотношение

Sk=S„(-* = 0,1,...,л-1. (8.58)

Коэффициент

= 1 4,

называют учетным коэффициентом дисконтирования.

Формулы (8.57) и (8.58) выражены в учетных периодах. Непосредственно во временной шкале они запишутся в виде

Stt^S,vh = Stt(l-dh), k = ,2,...,n, (8.57')

и

^=^vrs = Sjl-4p ft = 0,1, ...,«-1. (8-58'>

Как и для случая процентной модели, приведенную учетную модель можно распространить или продолжить с дискретного множества кратных точек на всю шкалу. По аналогии с процентной моделью можно рассмотреть три варианта продолжения:

кусочно-постоянная модель:

S,=S,(~df-m>, ,>х; (8.59)

непрерывная модель:

S^S,(-dhf^ t>x(8.60)

смешанная, кусочно-линейная модель:

S^S,{-d,,f-')lh\-dhr)lh, /£т. (8.61)

Ниже мы в основном будем пользоваться непрерывной моделью.

Заметим, что определяющим для учетной схемы является процесс дисконтирования (учета), а не роста. Таким образом, естественное направление времени в учетной модели противоположно естественному направлению в процентной модели, поскольку дисконтирование есть переход от будущего к прошлому.

Пример 8Л0. Пусть учетный период равен году, а учетная ставка за год 20\%. Если состояние накопительного счета в конце 10-го года равно .^5000, то каково состояние счета в конце 5-го и 3-го годов?

Решение. Согласно формуле (8.58), имеем

S5 = Sl0(] dhf = 5000(1 0,2)5 = 1638,40(.#)

и

5"3 = SJ dh)7 = 5000(1 0,2)7 1048,57(.3?).

Несмотря на естественность «обратного направления» времени, в

учетной модели можно, конечно, находить не только прошлые, но

и будущие (накопленные) значения счетов.

Пример 8.13. В условиях предыдущего примера найти состояние счета к концу 15-го года.

Решение. Согласно форімуле (8.58),

Отсюда получаем уравнение

5000 = SiS(0,8)5.

и, значит,

S1S=-^ = 15258,79(.*). В общем случае легко видеть, что при п > к

С — к _ с ./-я

или, вводя учетный коэффициент роста за период h

1

а*-~' (8.63)

получим

$.=ЗДГ, (8-64) в частности,

S^SQa"h. (8.65)

Так, для предыдущих примеров имеем h = 1, dh — 0,2 и, следовательно, за период h учетный коэффициент дисконтирования:

.;,= 1-</„ = 0,8,

а учетный коэффициент роста за тот же период

а,. = ~ = 1,25. * 0,8

Учетную ставку dh за период h можно задавать с помощью нормированной номинальной учетной ставки d, которая связана со ставкой за период соотношением

Число

1

т = — h

называют кратностью учета. При задании (нормированной) номинальной учетной ставки указывают либо учетный период Л, либо кратность учета т. В первом случае номинальная учетная ставка обозначается d а во втором — d{m Для краткости мы ограничились лишь определением нормированной номинальной учетной ставки с номинальным (учетным) периодом, совпадающим с базовым периодом временной шкалы. Ниже для упрощения записи прилагательное «нормированный» будем опускать. Кроме того, также как и для номинальной процентной ставки, основные результаты будем представлять в терминах номинальной учетной ставки d(m) с m-кратным учетом; при этом переход к явному указанию учетного периода h в соответствующих формулах производится заменой d(m) на d и /т на h,

В терминах номинальной учетной ставки для непрерывной учетной модели уравнение связи состояний накопительного счета имеет вид

*г=$(1-4)

(r-t)/h

1

т )

t>r.

(8.66)

В частности, собственно динамика накопления, выражаемая в непрерывной учетной модели формулой (t0 ~ 0)

t/h

0" ft

(8.67)

в терминах номинальной ставки <i(m) запишется как

' Л») Ym'

1

V

S{ iS"0

m j

(8.68)

По аналогии с процентной ставкой можно определить также нормированную эффективную учетную ставку (за единичный период временной шкалы) равенствами

1

(8.69)

т

Если необходимо подчеркнуть, по какому периоду или какой кратности учета эта ставка вычисляется, пишут d^ или dJ. Заметим, что

последнее определение эффективной учетной ставки носит общий характер, т.е. в нем h и т любые, хотя непосредственной интерпретации поддается лишь случай целого т. Если h = 1, т.е. период учета совпадает с единичным периодом временнбй шкалы, то учетные ставки всех трех видов совпадают:

d , = d. — dn. " d.

эф 1 Ш

Эффективной учетной ставке соответствует эффективный (нормированный) коэффициент дисконтирования

^ = 1 d h

эф эф

и эффективный (нормированный) коэффициент роста

1 1

(8.70)

а

эф

эф

эф

-d.

(8.71)

Для эффективных (нормированных) учетных ставок и коэффициентов дисконтирования и роста часто используют упрощенные (безиндекс-ные) обозначения, т.е. пишут d, v, а, если это не приводит к путанице.

П р и м е р 8.12. Рассмотрим учетную модель накопительного счета в годовой шкале с учетным периодом h =1/4, т = 4 и номинальной ставкой dw = 20\% годовых. Найти учетную ставку за период, а также соответствующую эффективную (нормированную) учетную ставку и соответствующие учетные коэффициенты дисконтирования и роста.

Решение. Поскольку номинальная учетная ставка J(4> = 20\% годовых учитывается 4 раза в году (т = 4), то учетная ставка за период учета, т.е. за квартал,

, d{A] 20\% ея/

За учетный период коэффициент дисконтирования

ущ = 1 0,05 = 0,95. Эффективный годовой коэффициент дисконтирования

и=(0,95)4 = 0,8145, соответственно годовая эффективная учетная ставка

d= 1 0,8145 = 0,1855, а эффективный (нормированный) учетный коэффициент роста

1

= 1,2277.

0,8145

Наконец, как и в случае процентной ставки, непрерывная учетная модель вида

і

V т )

для семейства учетных ставок d{m) с различной кратностью учета, но с одинаковым общим значением S = d(m) порождает предельный случай при т —» оо. Эффективный коэффициент дисконтирования

эф

т J

имеет предел

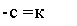lim v>j = lim

(

i_£T

Н _ Л-}

эф

(8.72)

Этому нормированному эффективному учетному коэффициенту дисконтирования соответствует нормированная (бесконечно-кратная) учетная ставка

/И

1-v

1-е"

(8.73)

и нормированный (бесконечно-кратный) коэффициент роста

Н ^ 5

I/1 ;

Таким образом, в обобщенной непрерывной модели с бесконечно-кратным (непрерывным) учетом по ставке д закон роста запишется в виде (/ 0)

S,=S0t*.

П р и м е р 8.13. Пусть в годовой шкале задана номинальная непрерывно начисляемая ставка 5= 20\%. Найти накопленное по этой ставке за 3,5 года значение суммы ,^?500. Решение. Нормированный коэффициент дисконтирования по этой ставке

а коэффициент роста и, значит

Si5 = 500eD'2'35 = 500 е°-7=1006,88(.#).

Таким образом, учетная модель накопительного счета вполне аналогична процентной модели. В обоих случаях текущее состояние счета выражается с помощью эффективных нормированных коэффициентов дисконтирования v или v либо роста а или а, для которых будем использовать безындексные обозначения. Разница лишь в том, что в учетной модели применяются учетные (эффективные, нормированные) коэффициенты дисконтирования и роста:

v = -d; a = v = —, (8.74)

где d — эффективная нормированная учетная ставка, а в процентной схеме используются процентные (эффективные, нормированные) коэффициенты дисконтирования и роста:

* = ! + /; v = a~]= —, (8.75)

где / — эффективная нормированная процентная ставка.

Сказанное означает, что, по существу, процентная и учетная модели идентичны. Различие состоит в выборе базового параметра для определения динамики накопления. В процентной модели — это ставка накопления /, в учетной — ставка дисконтирования </. Если коэффициенты роста или дисконтирования в обеих моделях совпадают, т.е.

а = а (8.76)

ИЛИ

v = d, (8.76')

то для любого начального состояния (О, SQ) обе модели описывают

один и тот же процесс:

St = Sdaf^sy (8.77)

или

S, = S0v" = S0v-'. (8.77*)

Условия (8.77), (8.77*) или равносильные им условия (8.76), (8.76') приводят к разнообразным соотношениям между ставками (как процентными, так и учетными), рассмотренными выше. Ставки, приводящие к одному и тому же процессу йакопления, называют эквивалентными в широком смысле. Для выяснения эквивалентности двух ставок достаточно выразить через них нормированные (в одной и той же шкале) коэффициенты роста (или дисконтирования). Если они совпадут, то исходные ставки считаются эквивалентными. Например, для эквивалентности ставок d{2) и /(3) необходимо, чтобы учетный нормированный коэффициент роста

(

ч~2

а

1

совпал с процентным нормированным коэффициентом роста

3

а

1 + -

V

т.е.

;-2

f3l Л3

3 )

Аналогично рассматривается эквивалентность других видов ставок.

Эквивалентность ставок в широком смысле позволяет не проводить строгого разграничения между различными типами моделей накопления. В частности, там, где это не приводит к недоразумениям, можно говорить просто о ставках, не уточняя, какой вид ставки имеется в виду, достаточно лишь помнить конкретный механизм построения модели накопления по любому виду процентной или учетной ставки. В этой связи в дальнейшем для обозначения коэффициентов дисконтирования или роста, как процентных, так и учетных, будем использовать одни и те же символы v, или а, соответственно.