8.9. стандартная схема сложных процентов

8.9. стандартная схема сложных процентов

Приведенные выше формулы для будущей и текущей стоимостей денежных сумм (событий) были связаны с конкретным типом финансового процесса в непрерывной модели накопления, задаваемого формулой где / — нормированная эффективная ставка накопления.

Эта формула, называемая формулой сложных процентов, — основополагающая для класса моделей, относящихся к схеме сложных процентов, т.е. моделей, финансовый закон для которых описывается вышеупомянутой формулой. Формальное описание финансовой схемы сводится к заданию:

финансовых законов, определяющих правила преобразования (приведения) финансовых событий и потоков;

семейства отношений эквивалентности, связанных с этими преобразованиями.

Финансовыми законами в стандартной схеме сложных процентов являются;

закон капитализации

A(t,p,C) = Ca(t,p), p>t, (8.109)

где

a(t,p) = ap~I (8.1І0)

и а > 0 — постоянный коэффициент, называемый нормированным коэффициентом капитализации (роста);

закон дисконтирования

D{ttp,C)=:Cv{ttp), p<t, (8.111)

где

v(/,/>) = v'-'

и v > 0 — постоянный коэффициент, называемый нормированным коэффициентом дисконтирования.

Таким образом, финансовые законы капитализации и дисконтирования стандартной схемы сложных процентов являются однородными относительно денежных сумм, непрерывными и стационарными (см. § 1.4). Будем считать также, что в стандартной схеме законы капитализации и дисконтирования взаимносопряженные, т.е.

<tP,t)

Условие сопряженности равносильно выполнению равенства v — v,

где V = I/O,

22-5169

т.е. коэффициенты капитализации (роста) а и дисконтирования v — взаимно обратны.

В нашей формулировке финансовых законов схемы сложных процентов нет никаких упоминаний о ставках.

На абстрактном уровне анализа они, собственно, и не нужны. Однако, учитывая возможные приложения схемы сложных процентов и содержательные модели финансовых процессов роста, на базе которых собственно и возникла сама схема, следовало бы определить понятие ставки, соответствующей финансовым законам схемы. Тем более что сделать это очень легко.

Так, нормированной процентной ставкой называется величина

i^a — I, а нормированной учетной ставкой

d= 1v.

Из этих определений немедленно следуют стандартные соотношения между этими ставками:

d- /= .

1+/ -d

Другие виды ставок (как процентных, так и учетных) получаются при преобразовании временной шкалы. Не будем здесь выписывать явные формулы для преобразования финансовых законов схемы сложных процентов и соответствующих им параметров (коэффициентов и ставок) при переходе к новой временной шкале, поскольку этот вопрос был подробно рассмотрен в предыдущих параграфах, посвященных различным видам ставок и их эквивалентностям. В этом параграфе временная шкала считается заданной и неизменной. Соответственно неизменными будут и параметры схемы (коэффициенты и ставки).

Два финансовых закона капитализации и дисконтирования порождают один общий финансовый закон:

К'" ' D(t,p,C), p<t,

получаемый «склейкой» законов капитализации и дисконтирования. Общий финансовый закон F(t, р, С) является, естественно, однородным (по С), непрерывным и стационарным законом. Причем условие

сопряженности законов капитализации и дисконтирования позволяют записать этот закон в виде

F(t,p,C) = Cap-!=Cvr-py

где t,p — произвольные моменты времени.

Перечисленные выше финансовые законы порождают преобразования финансовых событий, которые запишем в операторной форме.

Так, для любого события (Г, С) можно задать его приведенное к моменту р значение

PVp(t,C) = {p,Vp),

где

K,=nF(/,,,C) = CV-',

В тех случаях, когдар > /, говорят о будущем значении и пишут

{p,Vp) = FVp(t,C), а в случае р < t говорят о дисконтированном (текущем) значении

(p,Vp) = DVp(t,C).

Хотя общий оператор приведения PV и его частные случаи FV DVp представляют собой преобразования событий, на практике обычно говорят о преобразовании (датированных) денежных сумм и пишут просто

и соответственно или

Будем использовать эти сокращенные обозначения в тех случаях, когда это не будет приводить к недоразумению.

Показательный вид финансовых законов в схеме сложных процентов и соответствующих ему правил приведения FVz, DVt обусловливает дополнительно выполнение для последних так называемого свойства поглощения, которое сформулируем теперь для обобщенного оператора PVT.

Свойство поглощения оператора приведения. Для любого события (t, С) и любых тр т2

Доказательство этого свойства тривиально. Пусть

Ch=PVh{C) = C,vТогда

Содержательно (на языке процессов накопления) свойство поглощения означает, что различные траектории процентного роста для сложных процентов не могут пересекаться. Такое пересечение вполне возможно для процессов накопления по простым процентам. Другими словами, процессы накопления по сложным процентам «не имеют памяти» в отличие от процессов накопления по простым процентам. Будущее поведение такого процесса полностью определяется не только начальным, но и вообще любым состоянием этого процесса. Именно на этом факте основана упоминавшаяся выше простота теории сложных процентов.

Заметим, что в терминах § 1.4 упомянутое выше свойство поглощения есть следствие транзитивности финансовых законов капитализации и дисконтирования, т.е. для любого р из промежутка (т, г): ґ < /> < т имеет место соотношение

a(t,z) = a(t, р)а(р, г),

а для любого р из (г, t) х < р < t выполняется соотношение

d(t,z) = d(t, p)d(p. г).

Доказательство этих равентств вполне очевидно.

Задание правила преобразования (приведения) финансовых событий к произвольному моменту времени является лишь одной из компонент формального описания схемы сложных процентов. Вторая компонента состоит в определении понятия эквивалентности финансовых событий.

Эквивалентность финансовых событий в схеме сложных процентов.

Эквивалентность финансовых событий — второй важнейший аспект схемы сложных процентов. Возможность приведения (преобразования) событий позволяет тем или иным способом их отождествлять. Идея такого отождествления проста: события и соответствующие им денежные суммы считаются эквивалентными, равносильными и т.д., если их текущие значения, приведенные к некоторому моменту времени, совпадают.

Перейдем к формальным определениям. Пусть р — некоторый момент времени (полюс); / — нормированная эффективная ставка.

Определение 8.8. События {tv С,) и (/2, С,) называются эквивалентными относительно полюса р:

(',.С|)-('і.С,). если их текущие значения, приведенные кр совпадают:

(t,A)~(hA)<*PK{c>) = pvAci)

или в явной форме

Легко проверить, что так определенное отношение действительно представляет собой отношение эквивалентности, т.е. оно

рефлексивно: р

№)-№);

р р

симметрично: из (/1,С1)~(/2,С2) следует, что (г2,02)~»С|);

р р р

транзитивно: если (г,,С])~(ґ2,С2) и(/2,С2)~(/,С3), то (/,,С,)~(Г3,С,).

В данном определении эквивалентности подразумевается выбор точки приведенияр (полюса). Поэтому на самом деле в нем речь идет о семействе отношений эквивалентности, своего для каждого выбранного момента р. Однако в схеме сложных процентов все эти отношения, по существу, идентичны; два события, эквивалентные относительно одного момента времени, будут эквивалентными относительно любого другого момента времени, т.е. для любых т, и т2

Эта фактическая независимость (инвариантность) отношения эквивалентности от выбора момента приведения — простое следствие свойства поглощения оператора приведения. В самом деле, если события (гр С,) и (г2, С2) эквивалентны относительно момента времени г, то, согласно определению,

PKt(c,)=PV,(c2).

Применяя к обеим частям этого равенства оператор PVr приведения к любой другой точке т2, получим

pv,i(pk:(Q)=pK1{pK,(Q),

откуда на основании свойства поглощения следует ^(с,) = /\%(сг),

что означает эквивалентность событий (tv С{) и (iv С2) относительно г.

Из сказанного следует, что в схеме сложных процентов, по существу, имеется всего одно отношение эквивалентности финансовых событий, так что можно писать просто

(м ' ^1) ~ (^2 ' ^2 ) *

Конечно, при этом остается зависимость отношения эквивалентности от параметров финансовых законов.

В силу независимости выбора точки приведения при выяснении эквивалентности событий можно, в качестве этой точки брать моменты, соответствующие самим событиям. Таким образом, проверка эквивалентности событий (/,, С{) и (ґ2, С,), где t] < t2, сводится к проверке одного из следующих равенств:

прир-/

PV^C^FV^C^C, (8.112)

или в явной форме

при р — rf

pvti(c2)=q (8.113)

или в явной форме

Так, событие (1, 100) будет эквивалентно событию (З, 121) относительно ставки /'= 10\%, поскольку

100(1 + 0,1)2 = 121

или, что то же самое,

_Ш_= 100.

Заметим, что в терминах § 1.4 равенства (8.110), (8.111) определяют отношение непосредственной замещаемости событий. В общем случае это более сильное отношение, чем отношение эквивалентности относительно некоторой точки приведения. Так, для схемы простых процентов непосредственная замещаемость влечет эквивалентность относительно момента приведения, совпадающего с моментом одного из событий, но эквивалентность двух событий относительно некоторого момента времени, вообще говоря, не влечет их непосредственную замещаемость. Но в схеме сложных процентов эти отношения совпадают, т.е. непосредственно замещаемые события эквивалентны и, обратно, эквивалентные события являются непосредственно замещаемыми и, в частности, лежат на одной траектории процесса накопления, индуцированного более ранним событием.

Сказанное приводит к весьма простой геометрической структуре классов эквивалентности событий на плоскости время — деньги. Так, выбирая в качестве универсальной точки приведения начало временной шкалыр = 0, получим класс эквивалентности, содержащий события (О, С0), который состоит из событий вида (/, С), /є Т, где

С

^о^т.е. геометрически представляет собой кривую, являющуюся графиком показательной функции

ДМ

Семейство таких графиков для различных С0 и будет представлять собой геометрию отношения эквивалентности в схеме сложных процентов (рис. 8.5).

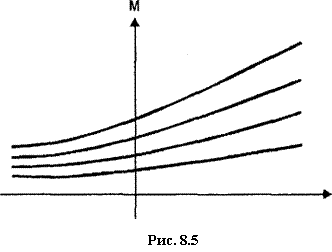Семейство этих кривых (или, как еще говорят, фактор-множество) образует разбиение плоскости время -деньги в том смысле, что, во-первых, их объединение дает всю плоскость и, во-вторых, эти кривые не пересекаются.

Наконец, легко видеть, что для моделей роста по сложным процентам каждая такая кривая содержит полностью

траекторию любого процесса накопления по ставке /, индуцированного любым состоянием (/0,С0), лежащим на этой кривой, как начальным состоянием этого процесса.

Данное выше определение эквивалентности относилось к финансовым событиям. Допуская вольность, часто говорят об эквивалентности (или неэквивалентности) денежных сумм. Конечно, в этом случае речь идет о «датированных», т.е. привязанных к определенным моментам времени, а не абстрактных суммах. При этом процентная ставка играет роль основного «финансового механизма», определяющего изменение стоимости или, точнее, ценности отдельной суммы со временем. Формально это изменение описывается с помощью введенных выше операторов преобразования (приведения). На практике же, конечно, оно реализуется с помощью инвестирования в конкретные финансовые или реальные активы. Речь, например, идет о вкладе в банке, покупке векселя, облигации, акции и т.п.

Подводя итог, можно сказать, что задание процентной ставки позволяет, во-первых, отождествлять события, относящиеся к различным моментам времени, во-вторых, «переносить» денежные суммы от одного момента времени к другому и, наконец, сравнивать суммы, относящиеся к различным моментам времени. '

Последнее утверждение нуждается в пояснении. Рассмотрим следующий вопрос: что больше — 100 или 9? 200? В такой постановке ответ на него очевиден. Сформулируем вопрос несколько иначе. Что предпочтительнее: #100 сегодня или #200 год спустя? Поскольку теперь суммы относятся к разным моментам времени, то непосредственно на него ответить невозможно. Инвестор, решающий такой вопрос, должен обладать способом сравнения таких сумм (событий!). Способ сравнения, конечно, субъективен и зависит от того, насколько инвестор нуждается в деньгах, может ли он позволить себе делать сбережения и т.п.

Однако если рассматривать этот вопрос с инвестиционной точки зрения, то он получает следующую трактовку. Стоит ли отказываться от .-#100 сегодня, чтобы получить в обмен на них #200 через год? Ответ на такой вопрос зависит уже только от инвестиционных возможностей. Так, если единственная возможность состоит в том, чтобы положить деньги в банк под 20\% годовых, то ответ, очевидно, положительный, поскольку по такой ставке сегодняшняя стоимость -#200 через год равна 200/1,2, что больше, чем #100. В этом смысле #200 через год предпочтительнее, чем #100 сегодня. Таким образом, указание процентной ставки позволяет привести суммы к одному и тому же моменту и затем осуществить сравнение.

Точно такая же ситуация возникает, когда мы хотим проводить арифметические операции над суммами, относящимися к различным моментам времени. Так, открыв счет на #200 в банке, дающем 20\% годовых, и добавив .#100 в конце года, вы получите, естественно, не просто арифметическую сумму

.-#200+ #100 = #300,

а иную величину, учитывающую эффект процентного роста:

.-#200(1 + 0,2) + ;-#100 = .#340.

С такого рода операциями приведения денежных сумм к одному и тому же моменту времени неоднократно столкнемся в дальнейшем.

Свойство поглощения оператора приведения и порожденная им независимость эквивалентности событий от полюса (момента приведения) приводит к тому, что в схеме сложных процентов относительный оператор приведения событий PV^ (см. § 1.5) совпадает с простым оператором PVr Напомним, что относительный оператор PVJp)

приведения событий к моменту г относительно полюса р преобразует данное событие (t, С) в единственное эквивалентное ему относительно полюса р событие (т, К). Поскольку выбор полюса для определения эквивалентности, как было показано, несуществен, то, полагаяр = т, в силу (8.112), (8.113) получим

PV}p) = PVp.

В схеме простых процентов (см. гл. 3) эти операторы существенно различны, что еще раз подтверждает большую простоту схемы сложных процентов по сравнению со схемой простых процентов вопреки их названиям.

Замечани е. Англоязычный термин compound interest указывает не на сложность (complexity), а на итеративный составной характер (compounding) начисления процентов.

На этом закончим изложение стандартной схемы сложных процентов. Напомним, что ее существенным моментом является постоянство коэффициентов (или ставок), определяющих финансовые законы схемы. На практике ставки, как правило, редко остаются неизменными. В последующих главах мы подробно исследуем процессы роста в нестационарных условиях, характеризующихся изменчивостью ставок. При этом основное внимание будет уделено общим и непрерывным схемам изменения ставок.