12.3. монотонные ренты

12.3. монотонные ренты

До сих пор мы ограничивались изучением постоянных рент или, более точно, рент с постоянными периодическими платежами. На практике часто используются ренты с переменными выплатами. Так, на рынке облигаций встречаются облигации с переменным (не путать с плавающим) купоном, по которым процентные выплаты (купоны) изменяются по определенным, заранее предписанным правилам. Переменные рентные выплаты встречаются в схемах погашения долга, например по закладным, при амортизации активов, в страховании и т.д. В этх>м параграфе мы рассмотрим специальный класс так называемых монотонных рент, в которых периодические платежи изменяются по определенному закону. Ограничимся двумя типами монотонных рент — арифметическими или линейными, в которых платежи изменяются по линейному закону, т.е. представляют собой арифметическую прогрессию, и геометрическими рентами, с показательным законом изменения платежей. В этом случае последовательность платежей представляет собой геометрическую прогрессию. В каждом случае, в зависимости от параметров закона изменения платежей, они могут возрастать со временем (говорят о возрастающей ренте) или убывать (говорят об убывающей ренте). Изучение монотонных рент начнем с анализа арифметических рент.

Арифметические ренты. В арифметической ренте платежи меняются со временем линейно и представляют собой арифметическую профессию где г ~ разность профессии, т.е. величина, на которую изменяются за каждый период платежи ренты.

Рассмотрим срочную стандартную арифметическую ренту. Ее период совпадает с единичным периодом временнбй шкалы и, следовательно, критические моменты ренты (концы ее периодов) имеют вид

tk = k, к = 0, 1,..., п.

Здесь для простоты мы выбрали начало ренты нулевым: tQ = 0. Тогда закон изменения платежей обыкновенной арифметической ренты будет иметь вид

C^p^ + rk, it =1,2,..., п. (12.45)

Следует обратить внимание на формулу (12.45) для платежей ренты. Согласно этой формуле, первый платеж ренты

а не ру Такой вид выражения для общего члена ренты выбран специально, для упрощения вывода формул стоимостей арифметических рент. Конечно, зная настоящий первый платеж ренты Сх и разность прогрессии г, легко найти рх

Это следует иметь в виду при использовании формул, которые будут получены ниже.

Если разность прогрессии г — положительна, т.е. г > 0, то рента возрастающая, если г — отрицательна, убывающая, если г = 0, то в этом (вырожденном) случае рента постоянная. Формула (12.45) показывает, что общую арифметическую стандартную ренту можно рассматривать как линейную комбинацию двух рент: единичной стандартной ренты Ап и арифметической ренты с платежами

Rk = к, к=,2,„.,п.

Эту возрастающую арифметическую ренту назовем канонической, или простейшей, и обозначим Ап, Здесь первый символ / есть начальная буква слова increasing, что значит «возрастающий».

Таким образом, поток платежей СУ7произвольной арифметической ренты есть линейная комбинация

CF=PlAn + rU (12.46)

двух рент.

Поскольку операторы стоимостей линейные:

/у (л А„ + rlA„) = a FVn (А„)+rFVn (IA„); (12.47)

PV0{p1A„+rlA„) = plPV0{k„) + rPVtl(IA„), (12.48)

то для нахождения стоимостей арифметических рент достаточно уметь находить стоимость канонической ренты ІА^.

Будущая (накопленная) стоимость стандартной арифметической ренты. Начнем с вычисления будущей (накопленной) стоимости ренты 1Ап. Будем считать заданной нормированную процентную ставку /. Если в качестве исходной задана какая-либо другая ставка, например номинальная, то сначала необходимо найти эквивалентную ей эффективную ставку, а затем работать с последней. Для заданной нормированной ставки /' накопленная к моменту п стоимость ренты 1Ап имеет вид

^Ди^-1(1 + /)п"Ч2-(1 + /)п"Ч...+^(1 + /)я"Ч...+« (12.49) или в сокращенной форме

^(1А„) = 2>

к=

где а = (1 + /) — нормированный коэффициент роста.

Накопленную стоимость канонической арифметической ренты обозначим или коротко Таким образом,

Величину при заданных параметрах ренты и ставке / можно подсчитать на компьютере или калькуляторе непосредственно по формуле (12.49). Мы выведем для нее более простую и компактную формулу. С этой целью умножим обе части (12.49) на коэффициент а = 1 + /, а затем вычтем почленно из полученного выражения исходное равенство (12.49). Тогда

als^ Is2 = (ап апЛ) + (іа"л la"'2) +... + (па п).

Раскрывая скобки и перегруппировывая слагаемые справа, получим

(a~l)Is^=an + (2ап~1 -ап-]) + (За"-2 -2ап~2)+ ...(па-(п-)а)-п

или

(я-1)/^ = а"+ап^+...+а-п.

Сумма первых п слагаемых справа есть накопленная стоимость авансированной единичной стандартной ренты:

Таким образом, получаем равенство

(fl-l)Zy-i =5-, -W

и поскольку а — 1-і, окончательно

Лл=-^-. (12.50)

Текущая стоимость стандартно» арифметической ренты. Из (12.50) легко получить выражение для текущей стоимости канонической арифметической ренты. В самом деле, меняя точку приведения с і = п на / = 0, согласно правилу переноса точки приведения, имеем

ЯК,(ІА„) = о"Л:(1А.),

где v — 1/(1 + /) = а~[ — нормированный коэффициент дисконтирования. Текущую стоимость простейшей (канонической) арифметической ренты обозначим 1а-,. Таким образом,

— п

la-1=vnh^vn-^ .

лі п і

Применяя еше раз правило переноса точки приведения, но уже к стандартной авансированной единичной ренте А„, получим

л ■■

v 5-, ап

и, значит,

а ~nvn

1а2=-^— • (12.51)

Содержательная интерпретация стоимостей стандартных арифметических рент. Выражения для стоимостей канонической арифметической ренты имеют простую содержательную интерпретацию. Для ее формулировки вспомним сначала содержательную интерпретацию формулы

(см. § 12.1). Эквивалентная запись этой формулы в виде (1+/)"=«д+1

означает эквивалентность двух схем погашения в момент t = п единичного долга, взятого в момент / — 0. В первом случае долг возвращается единовременно в момент «, и тогда величина выплаты равна (1+0\% т.е. левой части этого равенства. Во втором случае должник регулярно выплачивает проценты на взятую в долг сумму, а в конце срока возвращает основную сумму долга. В этом случае погасительные платежи представляют собой ренту с периодической выплатой / и единичным платежом в момент погашения / = п. Правая часть равенства как раз и дает накопленную стоимость этого потока платежей. От такой интерпретации легко перейти к интерпретации стоимостей канонической арифметической ренты.

Перепишем, например, формулу (12.50) в виде

Рассмотрим кредитную сделку, в которой должник занимает в начале каждого периода, т.е. в моменты t = 0, 1,..., /7—1 берет в долг единичную сумму ct = 1. Эти суммы представляют собой единичную авансированную ренту. Единовременная сумма погашення в момент t = п будет равна накопленной стоимости такой ренты, т.е. левой части равенства (12.52).

Эквивалентная схема выплаты долга состоит в периодической выплате процентов и возврате в момент погашения общей суммы долга. Поскольку в начале к-ю периода сумма основного долга будет равна к, то проценты за к-и период составят сумму ki. Таким образом, процентные выплаты образуют каноническую возрастающую ренту. Наконец, к моменту 1 ~ п общая сумма основного долга равна так что правая часть (12.52) дает накопленную стоимость всех погасительных выплат при таком способе погашения долга. Аналогично интерпретируется и формула (12.51) для текущей стоимости канонической ренты.

Текущая стоимость бессрочной стандартной арифметической ренты. Выражение (12.51) позволяет получить формулу текущей стоимости бессрочной возрастающей ренты с помощью предельного перехода

/«з-, = lim la-..

Поскольку

Wmnv" = 0 и 1ітйп = /d,

ТО

т 111

/а = — =_+_ di і і1

Так как

d= 1

1 + / то

т 1 1

Стоимости общих арифметических рент. Получив выражение для стоимостей простейшей арифметической ренты 1Ал, можем вернуться к общим арифметическим рентам вида (12.45). Используя разложение (12.46) и соответствующие ему формулы накопленной (12.47) и текущей (12.48) стоимостей, получим, что накопленная стоимость обыкновенной арифметической ренты с платежами вида

будет равна

^.(С-^АЪ+г&а,. (12.53) а текущая стоимость такой ренты имеет вид

pvt{cf) = pfi^+rl^,. (12.54)

Напомним, что если Сх — первый платеж арифметической ренты, то рх = Сх-г.

П р и ме р 12.18. Рассмотрим возрастающую арифметическую обыкновенную 10-летнюю ренту с выплатами в конце каждого года. Первая выплата равна #1000, а все последующие увеличиваются на 100. Найти накопленную и текущую стоимости такой ренты при ставке 10\% годовых.

Решение. Согласно условиям

Таким образом, Поскольку

я =10; С, = #1000; r= mOO. р] = 1000100 = 900(#).

, -М^!-15 937 ш~ 0,1 '

\%Я=1»Цд =17,531,

то

л^а —10

и, следовательно, накопленная стоимость ренты

FVi0 = 9ШЦд + 100ЛГп| = 21874,47(Ж).

Текущую стоимость найдем, дисконтируя полученную накопленную стоимость:

PV0 = (l,i)"w FVW = = 8433,55(.*).

В формулах (12.53) и (12.54) стоимости рент/г, не является первым платежом арифметической ренты. Выразим стоимости рент непосредственно через первый платеж Су Подставляя в (12.53) вместо р] выражение Cj — г, получим

^(СҐ) = С,,Й|+,(ЛЯ-,Я).

Но, согласно (12.50), Поскольку

то получаем еще одно выражение для обыкновенной арифметической ренты:

FV„(CF) = C^+r^. (12.55)

Меняя точку приведения t— п на t — 0 и соответственно умножая обе части на v", получим формулу для текущей стоимости арифметической ренты:

а„ -nv"

PV0{CF)^C^ +r^~f~. (12.56)

Последняя формула позволяет получить также текущую стоимость бессрочной обыкновенной арифметической ренты с первым членом С, и разностью г:

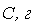
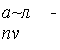PV0{CFoa)=lim С^ + г^Ч— =-^+-т. (12.57)

Пример 12.19. Найти стоимость бессрочной возрастающей ренты с платежами в конце каждого года, если первый платеж равен .#500, а все последующие увеличиваются на УЛ100 в год. Процентная ставка составляет 20\% годовых.

Решение. Согласно условию

С,= 3?500; /-=.#100; / = 0,2. Подставляя эти значения в (12.57), получим

5^100

0 0,1 0,01 v }

Убывающие арифметические ренты. В качестве первого примера убывающей срочной ренты рассмотрим так называемую простейшую (каноническую) убывающую ренту DAw с платежами вида

Ск — (п+) — к, к —1,2,..., п.

Убывающую ренту ВАп можно представить как частный случай общей арифметической ренты с параметрами С, = п и г = — 1. Тогда, согласно (12.55), накопленная стоимость такой ренты

$^-п n(a" -)-s^+n na"-s

Dsn = лзц «1 a ; i і

Таким образом, n(l+i)n -s

В свою очередь, из формулы (12.56) аналогичным образом можно получить выражение для текущей стоимости простейшей убывающей ренты:

Авансированные арифметические ренты. Выше мы ограничились изложением фактов, относящихся к обыкновенным немедленным арифметическим рентам. Однако рассмотренные методы оценивания стоимости обыкновенных немедленных рент дословно переносятся и на другие виды арифметических рент, например авансированные или отложенные. Так, платежи авансированной немедленной арифметической ренты с началом в /0 = 0 и сроком п имеют вид

Ck = C0 + rk, к = 0, 1,..., л 1.

В случае С0 = г =1 получается (простейшая) каноническая авансированная возрастающая рента 1АЧ с платежами

Ск = к+1, £ = 0, ],...,«1.

Ясно, что накопленная к моменту t — п стоимость этой ренты, обозначаемой через Is^, равна

FK„(IA„) = (1 + /)^,(IA„).

С другой стороны, очевидно, что ^(1А.)=*а,

следовательно,

/5д=(1+/)/5д. (12.58)

Обозначая текущую стоимость ренты 1А„ через /о^, получим для нее аналогичное соотношение

/ва=(і + і)/*1. (12.59)

Здесь мы меняли точку приведения. Другой подход основан на том факте, что авансированная рента получается сдвигом влево на один шаг (Т= -1) обыкновенной ренты, т.е.

1А„ = М1АЯ). Но тогда по лемме о сдвиге (см. гл. 10)

для любого г, что также приводит к соотношениям (12.58), (12.59).

Наконец, для стоимостей убывающей авансированной ренты DAW с платежами

Ск — п — к, к — 0, 1,..., п — 1, выполняются аналогичные соотношения

Д»а=(1+')ЛЪНе будем выписывать развернутые формулы для стоимостей этих рент, читатель может легко получить их самостоятельно.

Заметим, что мы снова сталкиваемся с правилом, связывающим стоимости обыкновенных и авансированных рент. Это правило является частным случаем общего правила, связывающего текущие стоимости двух смещенных друг относительно друга потоков с одинаковыми платежами:

PV,(LT(CF)) = vTPV,tT{CF),

где LT — оператор сдвига потока платежей; v — нормированный дисконтный множитель.

Так, еслиСЛ — обыкновенная немедленная рента, а Т~ -1, то 1Т(СА) будет соответствующей авансированной рентой, а если Т = m > 0 — отложенной (на срокт) обыкновенной рентой. Таким образом, приведенное соотношение позволяет единообразно получать формулы для различных вариантов монотонных рент.

Как неоднократно указывалось, в теории рент нет смысла запоминать различные формулы для стоимостей, их легко получить, если понимать основные принципы работы с потоками платежей. Изучение арифметических рент закончим примером.

Пример 12.20. Рассмотрим 20-летнюю обыкновенную ренту, состоящую из двух частей. Первая представляет собой 10-летнюю возрастающую ренту с ежегодными платежами в конце каждого года. При этом величина первого платежа равна J?5Q, а все последующие увеличиваются ежегодно на :#20. Вторая часть исходной ренты представляет собой 10-летнюю убывающую ренту с первым платежом в конце 11-го года, равным J?210, а все последующие уменьшаются на J?20. Ставка ренты равна 8\% годовых, начисляемых ежеквартально. Найти накопленную и текущую стоимости ренты.

Решение. Найдем сначала эффективную годовую ставку, соответствующую заданной номинальной ставке /(4) =

/ =

1=0,0824.

Исходную ренту можно рассматривать как сумму немедленной (возрастающей) и отложенной (убывающей) рент. Для вычисления стоимостей составной ренты поступим следующим образом. Выберем сначала в качестве момента приведения конец 10-го года, т.е. і = 10. Этот момент как раз разделяет ренту на две части: левую — возрастающую и правую —убывающую. Текущая стоимость S(l> левой (первой) части относительно t ] 0 есть просто накопленная стоимость возрастающей 10-летней обыкновенной арифметической ренты с первым платежом, равным и разностью — J?20. Поскольку

то, согласно (12.55),

(1 + 0,0824 -1

s = i : 1 = 14,654,

101 0,0824

ha-10)

S{1) = S0sT(i + 20v " 1 = 1862,59р?).

Текущая стоимость /*2) относительно t = 10 правой (второй) части ренты есть текущая стоимость обыкновенной (убывающей) арифметической ренты с первым платежом :#210 и разностью — J?20. Поскольку

^=^=6,637,

то, согласно (12.56),

Р*2) =2