1.2. финансовые события и денежные потоки

1.2. финансовые события и денежные потоки

Финансовые события и платежи. Введем теперь два понятия, которые образуют своеобразный мостик между финансовыми величинами двух классов, введенными в предыдущем параграфе. Речь идет о финансовых событиях и финансовых (денежных) потоках.

В финансовой математике, как уже упоминалось, сопоставляются денежные суммы и моменты, или промежутки, времени, к которым они относятся.

Определение 1.L Пара (t, С), состоящая из момента времени / и значения суммы С, называется мгновенным финансовым событием или событием J-го рода. Мгновенные события будем называть просто событиями.

Финансовое событие наглядно изображается либо отмеченной точкой на временной диаграмме, либо точкой на плоскости время-деньги (см. рис. 1.5).

Финансовое событие может иметь различную интерпретацию. Так, это может быть просто указание стоимости актива в данный момент времени. Но это может быть и взнос (вклад, поступление) на счет или в фонд в некоторый момент ї определенной суммы С. Это может быть также выплата (изъятие) со счета или фонда некоторой определенной суммы в момент времени t. В первом случае значения С обычно записываются положительными, а во втором случае — отрицательными числами.

Определенные выше события (1-го рода) являются формальным представлением мгновенных финансовых величин. Интервальные финансовые величины представляются событиями 2-го рода.

Определение 1.2. Пара (У, С), где J с Т — некоторый временной промежуток, а С є М — денежная сумма, называется интервальным событием или событием 2-го рода.

На временной диаграмме интервальное событие изображается, как

на рис. 1.6.

Хотя мы определили два вида

?1 J 2 финансовых событий, соответствуРис. 1.6 ющие двум типам финансовых величин, на практике во многих случаях, как, в частности, отмечалось в примере с выплатой дивидендов, можно обойтись событиями 1-го рода. Так обычно и поступают. Для этого используют преобразование интервального платежа в мгновенный платеж:

. (У,С)->(т,С).

В простейшем случае величина платежа не меняется, а преобразование заключается в выборе момента т актуализации этого платежа. На практике чаще всего используются два правила актуализации интервального платежа (У, С), где J — промежуток с концами tp tr В первом случае платеж С осуществляется в начале промежутка, т.е. т= t Такая схема актуализации называется авансированием (рис. 1.7а). Во втором случае платеж С осуществляется в конце промежутка, т.е. г = t. Эта схема называется финализацией (рис. 1.7 б).

с с

1 1 1 1

а б Рис. 1.7

Актуализация задает способ преобразования событий 2-го рода в события 1-го рода. Имеется еще один вид связи между такими «разнородными» событиями, состоящий в преобразовании событий 1-го рода в события 2-го рода. Речь идет об операторе изменения мгновенной величины за некоторый промежуток времени J = [tv t2. Если нам известны два события (tv S{), (tv S2) (1-го рода), соответствующие состояниям фондовой величины в моменты tp tv то можно определить событие 2-го рода (/, С), где С — LSS— S(t2) S^) — изменение величины ^на промежутке /.

Финансовые потоки. На практике изолированные события рассматриваются редко. В большинстве случаев в финансовой сделке участвует не одно, а множество событий.

Определение L3. Последовательность

{('рС,),('2.С2),...,(г„,С„)},«<

со

финансовых событий называется (дискретным) финансовым или денежным потоком 1-го рода и обозначается символом CF(от англ. cash flow).

При п < ос — это конечный (дискретный) финансовый поток. В финансовой литературе рассматривают также и случай п = <», т.е. бесконечные (дискретные) потоки, например так называемые вечные ренты.

Так, открытию счета на 1000 и последующему снятию с него в конце 1-го и 2-го годов соответственно шаоо и У>?300 соответствует финансовый поток

CF = {(0,1000),(1, -400), (2, -300)}.

Денежный поток наглядно изображается либо последовательностью отмеченных точек на временной шкале (рис. 1.8 а), либо точками на координатной плоскости (рис. 1.8 6).

М

■> Т

б

Рис. 1.8

Изображения финансовых событий и потоков на временной шкале называют обычно временными диаграммами, а их изображения на плоскости — графиками.

Естественным образом определяются умножение финансового потока на некоторое число и сумма (объединение) двух финансовых потоков. Так, под результатом умножения финансового потока

C/r = {(/„Cl),(r2,C2),...,(/„,C„)} на число а понимается поток

aCF = {(/, ,оС1 ),(*2,аС2),... ,(t„,aC„)}. В свою очередь, результатом суммирования потоков CF и CF

является поток CF] + CF2, состоящий из всех финансовых событий (/j'C^) и (ф,С]Р), входящих в потоки CFX и CF2 соответственно, для

которых моменты t{p и tf^ различны, а также событий (/у,С^+CJ2)) при tf^ = /f* = tj. В последнем случае, если в результате сложения сумм

имеем, что + Cf^ = 0, то событие (л, 0) можно не включать в результирующий поток.

Моменты времени /, для которых имеют место ненулевые платежи, назовем критическими моментами. Таким образом, если t — критический момент, то в финансовом событии (л, С) должно выполняться условие С. * 0.

Пример 1.1. Для финансовых потоков событий

CFl = «0, 100), (2, -200), (3, 400), (5, 100), (6, -300)}

и

CF2 {(2, 400), (4, 700), (5, -150), (6, 650), (7, 800)}

найти финансовый поток 2С7Г1 + CFr

Решение. Прежде всего выпишем поток 2CFS:

2CFX = {(0, 200), (2, -400), (3, 800), (5, 200), (6, -600)}. Тогда для потока 2CF; + CF2 окончательно получаем

2CF] + CFX = {(0, 200), (3, 800), (4, 700), (5, 50), (6, 50), (7, 800)},

при этом событие (2, 0) опускается, так как моменту времени f = 2 реально никакого финансового значения не приписано.

Заметим, что в финансовой математике дискретный денежный

поток часто описывают не последовательностью {h^k)}"k t составляющих этот поток событий, а его денежной или платежной функцией Сс= С(Г):

С:Т->М, /->C(f),

определенной на всей временной шкале. При этом функция C(t) ~ 0 во всех точках, кроме критических, в которых она, естественно, совпадает с суммами С , связанными с событиями, т.е.

с(/)=

0, если t±tk

Ск, если t = tk,

Функции такого рода принято называть финитными (для конечных потоков), поскольку они отличны от нуля лишь в конечном числе точек. Множество всех точек (моментов), в которых характеристическая функция потока отлична от нуля, называется его носителем и обозначается suppC/7:

suppC/, = {reT|C(/)^0}={rM/2s...,/e}.

С помощью денежных функций легко определяются алгебраические операции над потоками. Пусть, например, С,(0 и C2(t) — денежные функции потоков CFX и CF2 соответственно. Тогда для потока CF, являющегося суммой

CF = CFX+CF2

этих потоков, денежная функция C{t) определяется равенством

C(/) = Q(/) + C2(/).

Анатогично денежная функция C{t) потока ACF, полученного умножением потока СТна число Я, есть произведение денежной функции С(0 потока CFna это число:

С(/)=ЯС(/).

Согласно данному выше определению потока, его события относятся к определенным моментам времени. Рассмотрим упоминавшуюся выше выплату дивидендов по акциям (или процентов по облигациям). Последовательность ежегодных выплат дивидендов можно также описать денежным потоком. Но дивиденды по своему содержанию являются выплатами за период, например за год. Поэтому с формальной точки зрения следовало бы определить еще один вид потоков, состоящий из платежей за период.

Определение 1.4. Интервальным финансовым потоком или денежным потоком 2-го рода называется последовательность событий 2-го рода

CF = {(J„Cl),(J1,CJ),...,(J.,C.)}.

где Ур У / — попарно непересекающиеся промежутки времени.

На временной диаграмме (рис. 1.9) приведена графическая иллюстрация денежного потока 2-го рода.

С1 с2

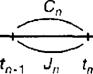
Рис. 1.9 100 200 300 Определенная выше операция

^ ^ ^ актуализации событий 2-го рода

_і 1—,—,—і 1

легко переносится и на потоки.

0123 Применяя ее к каждому собыРис-110 тию, из потока 2-го рода получим

100 200 300

—I і hпоток 1-го рода, т.е. обычный поток событий. Хотя в принципе

1 выбор конкретной схемы актуа0 12 3 лизации (авансирования или фиРис. 1.11 нализации) может быть различным для различных событий, на 100 200 300 практике обычно используют

«единообразную» схему актуали' 1 1 1 зации: либо авансирование для

0123 всех событий, либо финализация

Рис. 1.12 также для всех событий потока

2-го рода.

Таким образом, в первом случае интервальный поток CF превратится в авансированный (относительно последовательности промежутков J,) поток событий

к'

СР={{1,,СУ{Ц,С2),...,{(ПА,СП)},

а во втором — финансированный поток

С^={(^С,),(Г2,С2),...,(/„;СЛ)}.

Оператор авансирования обозначим через Adv, а оператор финализа-ции через Fin. Тогда

CFa = Adv(CF);

CFf =Fin(CF).

Пример 1.2. Для потока 2-го рода (рис. 1.10) найти соответствующие этому потоку авансированный и финализированный потоки событий. Решение. Авансирование потока СТдает поток

CFa = AdvifP) = {(0,100),(1,200),(2,300)}

Его диаграмма приведена на рис. 1.11. Финализация потока С7-*дает поток

CFJ = FinifF) = {(1,100),(2,200),(3,300)},

диаграмма которого показана на рис. 1.12.

Можно также рассматривать преобразование потоков 1 -го рода в потоки 2-го рода. Один из общих подходов к такому преобразованию будет описан ниже, а здесь рассмотрим преобразование потоков, связанное с понятием изменения фондовой величины. Пусть

Cf = {(/I,C1).(/2,C1),...,(r„C,)}

— поток событий, представляющий собой последовательность состояний некоторой фондовой величины. Тогда ему соответствует поток 2-го рода

cf={(y1,q),(/J,c!),...,(/„c,)},

где Jk = [tkJk+]],aCk = ASk = S(tk+l)S(tk) — изменение S на промежутке Jk.

Описанные операции чаще всего используются в теории рент, являющихся примерами так называемых регулярных потоков платежей.

Ренты. Регулярные потоки платежей естественным образом появляются во многих финансовых контрактах, сделках и операциях. Выплата процентов по облигациям или по вкладу, выплата дивидендов акционерам, выплата пенсий участнику пенсионной схемы — все это примеры регулярных потоков платежей. В понятии регулярности потока есть два аспекта: временной и финансовый. Временной аспект связан с регулярностью моментов осуществления платежей, например, платежи осуществляются в конце каждого месяца, квартала или года. Финансовый аспект связан с некоторой закономерностью в размерах самих платежей, например, все платежи одинаковы, платежи монотонно растут на заданную величину, или увеличиваются в заданное число раз, или, наоборот, уменьшаются и т.п.

Обычно потоки платежей, обладающие регулярностью платежей как по времени, так и по величине, называют рентами. По своему смыслу рентные платежи, как отмечалось выше, являются интервальными величинами, поскольку относятся к периодам, а не моментам времени. Поэтому рента — это регулярный поток платежей второго рода. Выше было показано, как этот поток превращается в обычный поток платежей (поток 1-го рода или поток событий), который также называется рентой. Поскольку ренты играют очень важную роль в финансовом анализе, рассмотрим их более подробно. Начнем с определения.

Определение 1.5. Рентой называется интервальный поток (поток 2-го рода)

CF = {(y„C1),...,(/„,C„),...}

с последовательностью смежных промежутков

Л'--'Л»*--'Л'---'

называемых периодами ренты, одинаковой длины:

Jt = JA = ... = J = h. Число h называется (числовым) периодом ренты. Концы

промежутков

называются (критическими) моментами ренты. Они образуют арифметическую прогрессию tt = t0+nh, /1 = 0,1,.... Момент г называется началом ренты. Если рента имеет конечное число промежутков Jk (или платежей), то она называется срочной, в противном случае — бессрочной, или вечной. Конец tn последнего промежутка Jn срочной ренты называется концом ренты. Число T=tn—tQ называется горизонтом (шириной) ренты.

Некоторые платежи ренты могут быть нулевыми. Периоды, которым соответствуют ненулевые платежи, называются платежными, остальные периоды — нулевыми (пустыми). Число платежных периодов называется сроком ренты.

Начало первого платежного периода ренты называется эффективным началом, а конец последнего платежного периода — эффективным концом ренты.

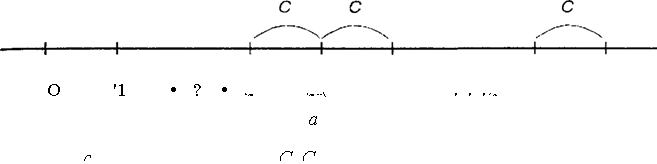
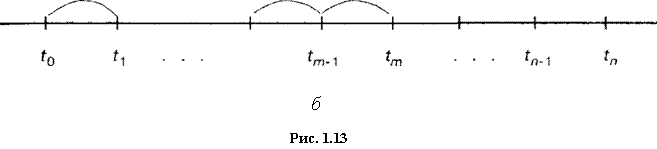
Таким образом, начало и эффективное начало ренты могут не совпадать. При совпадении рента называется немедленной, в противном случае — отложенной, или отсроченной. Если конец и эффективный конец ренты совпадают, то рента называется завершенной, в противном случае — незавершенной. На рис. 1.13 изображены диаграммы отложенной (а) и незавершенной (б) рент.

Если все ненулевые платежи ренты равны, то рента называется постоянной. Если платежи ренты монотонно растут, то рента называется возрастающей, если монотонно убывают, то — убывающей; и в том, и в другом случае рента называется монотонной. По характеру монотонности (убывания/возрастания) ренты делятся на арифметические

и геометрические. Платежи арифметической монотонной ренты составляют арифметическую прогрессию

Cjw=Cfc+^ А'= 1,2,...,

а платежи геометрической монотонной ренты образуют геометрическую прогрессию

Сы=СкЯ, (q*0), *=1Д... _

Приведенные выше определения задают ренту как поток CF 2-го рода. Но на практике рента реализуется (актуализируется) как поток финансовых событий. Выше мы привели два правила актуализации, т.е. превращения интервального потока в поток (ренту) событий.

В первом случае все рентные платежи относятся на начала соответствующих периодов. Полученный таким преобразованием ноток называется авансированной, упреждающей рентой или рентой пренумерандо.

Во втором случае все рентные платежи относятся на концы соответствующих периодов. Полученный таким преобразованием поток называется финальной, обыкновенной рентой или рентой постнумерандо. Обыкновенную ренту в отечественной литературе [24] иногда называ-ют задержанной. Термин «задержанная рента» не следует путать с ранее приведенным термином «отложенная (отсроченная) рента».

На оба описанных выше представления интервальной ренты как потока событий дословно переносятся все данные выше определения. Так, можно говорить о срочной постоянной обыкновенной ренте, отложенной возрастающей авансированной ренте и т.д.

3-5169

Периоды ренты на практике обычно связаны с так называемыми стандартными календарными периодами, подробно рассматриваемыми ниже в этой главе. К ним относятся годовые, полугодовые, квартальные, месячные и т.д. промежутки. Ренту с годовым периодом обычно называют аннуитетом.

Иногда суммы, относящиеся к естественным периодам ренты, реализуются не одним платежом, а серией одинаковых (более мелких) платежей, равномерно распределенных по периоду ренты. Так, дивидендная рента по акциям с естественным годовым периодом часто выплачивается ежеквартально. Другим примером может служить купонная рента по облигациям. Годовой процент по облигациям, задаваемый купонной ставкой, часто выплачивается двумя одинаковыми платежами по полугодиям. Ренты такого вида называютсяр-кратными относительно базового периода ренты (обычно года). Так, р-кратная рента с годовым периодом (т.е. аннуитет) и годовым платежом С реализуется в виде р одинаковых платежей величины С/р. Эти платежи сами образуют ренту, которую назовем микрорентой, соответствующей базовому периоду ренты (рис. 1.14).

С/р С/р

С/р

н

к-1+2/Р ■ ■ ■ Рис. 1.14

Vi+<P-1)/P tk

Микрорента получается дроблением суммы С, относящейся к некоторому базовому периоду. Если эта операция выполняется для всех сумм и периодов ренты, то полученная рента называется р-кратным дроблением исходной ренты. Оператор р-кратного дробления обозначим как Dip соответственно ренту, полученную /?-кратным дроблением ренты CF , как В[р) (СУ7). _

Пример 1.3. Для арифметической возрастающей интервальной ренты CF (рис. 1.15) найти микроренту, соответствующую трехкратному дроблению последнего платежа, и ренту, полученную двукратным дроблением всей ренты CF .

100

200

300

100

100

100

+

+

о

1 2 Рис. 1.15

7/3 8/3

Рис. 1.16

Решение. Микрорента D&([2, 3], 300), соответствующая трехкратному дроблению последнего платежа, изображена на рис. 1.16.

Рента />(2,(ст), получающаяся двукратным дроблением ренты CF, показана на рис. 1.17.

50 50 100 100 150 150

0 1/2 1 3/2 2 5/2 3

Рис. 1.17

К дробной ренте, т.е. ренте, полученной />-кратным дроблением, можно применить оба вида преобразования (актуализации), которые рассматривались выше. Последовательно применяя операторы дробления и актуализации, можно получить дробные ренты событий. Так,

ренту Adv{o^ (cF)) можно назватьр-кратной авансированной рентой, а ренту Fin{D^ (CF)) ~ р-кратной обыкновенной рентой.

Пример 1.4. Для интервальной ренты CF из предыдущего примера найти различные актуализации двукратного дробления этой ренты. Решение. Очевидно, что

AdvdP]{CF)) = {(0,50), (1/2, 50), (1, 100), (3/2, 100), (2, 150), (5/2, 150)}.

Аналогично

Fin(D{1]{CF))= U1/2, 50), (1, 50), (3/2, 100), (2, 100), (5/2, 150), (3, 150)}.

Мы определили оператор дробления непосредственно для интервальной ренты. Очевидно, что его легко распространить на ренты событий. Для этого необходимо просто поменять местами операторы дробления и актуализации.

Так, р-кратное дробление авансированной ренты (событий) можно определить как авансирование кратного дробления исходной интервальной ренты:

D{p) [AdviCF)) = Adv{D[p) (CF)). Аналогично можно определить дробление обыкновенной ренты

(событий): ^{Fin{cF))=Fin{D4CF)).

На этом закончим краткий обзор основных понятий, относящихся к регулярным потокам — рентам.

Большое внимание, уделенное финансовым событиям и потокам, вызвано тем, что в современной финансовой теории понятие актива непосредственно связано с понятием потока платежей. По существу, с формальной точки зрения любой актив можно представить порождаемым им потоком платежей. Так, облигацию можно описать потоком, состоя щим из всех процентных выплат и выплаты ее номинала в конце срока погашения, акцию можно отождествить с потоком выплат дивидендов и, в случае продажи, вырученной суммой, недвижимость — потоком арендных платежей и т.д.

Рассмотрим, например, облигацию с номинальной стоимостью .#1000 и сроком погашения 3 года. Пусть купонная ставка равна 8\% годовых и проценты (купоны) выплачиваются дважды в год в конце каждого полугодия, т.е. по истечении очередного полугодия требуется выплатить № 40. Тогда денежный поток, порождаемый этой облигацией, имеет следующий вид (рис. «1.18).

40 40 40 40 40 1040

—I 1 і 1 1 і I—

0 1/2 1 3/2 2 5/2 3

Рис. 1.18

Представление актива в виде денежного потока позволяет строить математические модели, описывающие количественные соотношения между основными характеристиками активов: их ценами, доходностью, риском и др. Ниже будут рассмотрены некоторые из таких моделей.

Нетто-величина дискретного потока и простейшие балансовые модели. Согласно определению, финансовые события, составляющие поток платежей 1-го рода, относятся к конкретным моментам времени. Введем теперь характеристику, связанную с событиями потока, происходящими внутри некоторого промежутка времени.

Определение 1.6. Нетто-величиной потока платежей

c/r={(f„cl),(/,,c3),..,(f„,c.)}

на промежутке J называется величина

NV(CFJ)=JJCt,

т.е. это просто алгебраическая сумма величин С тех платежей потока, моменты времени которых попадают в данный промежуток; символ NVсокращение от англ. netto-value.

Заметим, что здесь при определении промежутка времени важно указать, включаются ли в него или нет его границы. Например, для потока

CF= {(-3, 100), (-1, 200), (1, 300), (2, 400)} для различных промежутков можно вычислить соответствующие нетто-величины потока:

NV(CF, [-4, 0]) = 100 + (-200) -100; NV(CF,(~l, 1]> = 300;

NV(CF, [-3, 5)) = 100 200 + 300 + 400 600.

Для нетто-величины потока имеет место очевидное свойство. Свойство аддитивности. Для любых ti<t2< ^

NV{CF, [tv t2])+NV(CF, (tv ф = NV(CF, r fj),

т.е. нетто-величина потока на промежутке равна сумме нетто-величин потоков на составляющих этот промежуток непересекающихся под-промежутках (т.е. его частях).

В финансовой математике широко используются так называемые накопительные модели. Такой простейшей моделью является модель накопительного счета (или фонда), состояние которого в момент t предстявляет собой мгновенную денежную величину S{t). Поступающие на накопительный счет средства, задаваемые входным потоком платежей, аккумулируются на счете, увеличивая его состояние, соответственно снимаемые со счета средства образуют выходной поток уменьшающий состояние счета. Наличие входного и выходного потоков, таким образом, тесно связано с изменениями состояния счета. Более того, само понятие состояния в этом случае нуждается в уточнении. Для пояснения этого рассмотрим следующий пример.

Пусть инвестор имеет на счете в банке .#500. В некоторый момент времени tQ он вносит еще УЯ100. Каково состояние счета в этот момент времени? Следует помнить, что мы имеем дело с моделью, т.е. идеализированным представлением процесса формирования счета. Поскольку в модели поступление новой суммы считается мгновенным, то мгновенно должно измениться и состояние счета. Таким образом, возникает «неопределенность»: считать ли состоянием в момент времени tQ начальное значение .#500 или же новое «пополненное» значение ^?600? На практике такой вопрос, конечно, не возникает, поскольку пополнение счета не мгновенный акт, а процесс, имеющий длительность. Однако в математической модели необходимо сделать выбор и дать соответствующее определение состояния. В принципе возможны tnpu варианта.

В первом из них предлагается считать состояние просто неопределенным в моменты поступления или изъятия сумм, но этот подход не очень удобен.

Во втором варианте состояние в момент / совпадает с «непосредственно предыдущим». Математически это записывается в виде

S(y = 5(/0-0),

где

S(L -0)= lim S{t)

есть предел слева S(t) в точке tQ. Это значит, что функция S(t) является непрерывной слева в точке t

Для нашего примера это соответствует выбору состояния счета в момент tQ, равного J? 500.

Наконец, в третьем варианте состояние в момент tQ считается совпадающим с «непосредственно следующим за ним» состоянием. Это значит, что

S(tQ) = S{t0 + 0),

где

S(L +0)= lim S(!)

есть предел справа функции S(f) в точке f. В этом случае S(t) непрерывна справа.

В нашем примере это соответствует состоянию счета в момент tQ, равному ^600.

Таким образом, во втором варианте состояние счета в момент tQ «не реагирует» на поступление, а в третьем варианте оно — «завершенное», т.е. то, в котором уже учтено поступление на счет, произошедшее в данный момент времени.

Следует отчетливо понимать, что вопрос о том, «какое состояние на самом деле», бессмыслен. Но, строя математическую модель, необходимо дать соответствующее определение состояния.

Здесь и в последующем выбираем третий вариант — завершенное состояние. Если бы выбрали второй вариант, то промежутки в свойстве аддитивности были бы открытыми справа, т.е. имели вид [rp t2) и [t t3).

Нетто-стоимость потока, как легко видеть, полностью определяет сам поток. В самом деле,

C=NV{CF, kJk]).

Таким образом, нетто-стоимость является еще одной и, как увидим ниже, более общей формой задания финансовых потоков.

Финансовые или денежные потоки обычно имеют источники, т.е. финансовые средства, ресурсы, запасы, которые порождают эти потоки, и приемники или цели, куда эти потоки поступают. Источники и приемники можно представлять в виде резервуаров, накопителей денежных ресурсов, т.е. с позиции финансовой математики это просто фонды. Текущая величина (объем) фонда есть стоимость имеющихся в данный момент в фонде активов. Это — величина 1 -го класса. Денежный поток, связанный с фондом, может менять его величину в течение некоторого промежутка времени. Если положительные значения из потока рассматривать каквходной поток, а отрицательные — каквыходной, то исходный денежный поток разобьется на два потока: один поступающий (втекающий) в фонд, а другой исходящий (вытекающий) из него. Заданный промежуток времени изменение величины фонда в точности равно алгебраической сумме платежей потока за этот же промежуток.

Математически этот факт отражается следующим образом. Пусть VQ— начальная величина фонда; К — величина фонда в момент времени Л Тогда для любого потока CF, связанного с фондом, будет справедливо соотношение

VrV0 + NV(CF,(Q,t) t>0, (1.1)

которое называется уравнением баланса.

Далее, пусть t{ и t2 — произвольные моменты времени и t < t Тогда из (1.1) с учетом свойства аддитивности нетто-величины потока событий следует, что

V,!=V0+NV(CF,(0,t1]) = V0+NV{CF,(0,Il}) +

+NV(CF,(tl,,2}) = V,[+NV(CF,(tlj2}).

Таким образом, получим соотношение

V^V^NViCF^t,]), 1,<12, (1.2)

которое также называется уравнением баланса.

Уравнение (1.2) есть просто выражение закона сохранения. В самом деле, разность У, -Vti есТь изменение объема фонда за промежуток времени (/ t2, а объем фонда в этом промежутке изменится ровно настолько, сколько денежных средств поступит (или уйдет) в (из) него. Нетто-величина потока как раз и дает общий баланс поступлений и изъятий фонда.

В качестве примера рассмотрим снова поток

CF = {(-3, 100), (-1, 200), (I, 300), (2, 400)}.

Считая, что величина фонда в момент времени / = 0 составляет V0 = :^500, можно найти состояние фонда в любой другой момент времени. Так,

Vl = V0 + .-#300 :\%500 + .-#300 = .#800;

v3 = v{ + тоо= улпоо

и т.д.

Приведенные выше определения и вычисления, отражающие зависимость величины фондов от соответствующих потоков финансовых событий, не учитывают временную стоимость денег. Это чисто балансовые соотношения. Существуют более сложные соотношения, учитывающие и фактор времени в том смысле, о котором говорилось ранее. Так, величина фонда может изменяться не только из-за временных поступлений, но из-за изменения стоимости активов фонда.

Общие финансовые потоки. В заключение параграфа проанализируем финансовые потоки с несколько более общей точки зрения, позволяющей ввести обобщенное понятие финансового потока и, в частности, описать так называемые непрерывные потоки, которые играют важную роль в финансовом анализе.

Рассмотренные выше потоки событий (потоки 1-го рода) являются дискретными (или сосредоточенными) потоками, потоки 2-го рода — интервальные потоки, являются распределенными. Между ними имеется двусторонняя связь. Интервальный поток CF можно (вообще говоря, искусственно) преобразовать в дискретный, а любой дискретный поток (событий) CF — в интервальный, если некоторым образом подобрать последовательность непересекающихся промежутков /j,/,,...,/, содержащую все моменты дискретного потока. В этом случае промежутку Jk можно поставить в соответствие интервальный платеж

Ck^NV(CFJk),

являющийся нетто-значением потока CFна промежутке Jk. Эта связь имеет более глубокие корни; она позволяет дать обшее определение финансового потока, включающего как дискретные, так и распределенные, в частности, непрерывные потоки.

Задать финансовый поток общего вида можно с помощью так называемой величины потока — функции, сопоставляющей каждому промежутку / временной шкалы Т значение V{J) величины потока, соответствующее этому промежутку. Содержательно величина потока для данного промежутка равна общей денежной массе, «перенесенной» потоком за данный период времени. Формально это просто некоторая функция промежутков времени. Ее естественно считать аддитивной в том смысле, что величина потока для промежутка, разбитого на две части, будет равна сумме величин потоков, соответствующих этим частям. Таким образом, можно дать следующее определение.

Определение 1.7. Величиной финансового потока CF называется аддитивная функция VZF промежутков временной шкалы Т, т.е. функция VCf, сопоставляющая каждому промежутку J (любого вида) некоторое значение Vcr(J) из денежной шкалы М. Аддитивность VCF означает, что для любых двух непересекающихся промежутков /, /2, дающих в сумме промежуток/:

/=ли/2, /,пу2=0,

выполняется равенство

^т(у) = к„(у1ил)=кс,(/1)+|/„(/2).

Поток СТ7, определяемый своей величиной V , назовем общим финансовым потоком.

В дальнейшем величину потока будем обозначать как К, если это не будет приводить к недоразумениям.

Определение общего финансового потока весьма похоже на определение потока 2-го рода, однако в нем нет упоминания о какой-либо заранее заданной последовательности смежных промежутков. Значение величины финансового потока (или объем платежа) сопоставляется любому промежутку.

Введем еще ряд дополнительных определений, связанных с понятием общего финансового потока, которые позволят точнее описать связь этого понятия с ранее изученными потоками.

Как и для дискретных потоков, можно определить операции над общими потоками. Так, говорят о сумме CF ~ CF{ + CF2 двух общих потоков, задаваемых величинами Vx-VCf и V2 = VCF, соответственно. При этом для каждого промежутка/величина V(J) VCF(J) суммарного потока определяется суммой значений V{(J) и V2(J), т.е.

У(Г>=У{(/) + У2(/).

Умножение общего потокаCF, задаваемого величиной V— VCF, на число Я дает поток ЯС/7, значение величины которого для промежутка/равно ЯК(/).

Будем говорить, что точка а є Т является особой или критической точкой потока, если для любых достаточно малых промежутков /, содержащих а, имеет место равенство

V(J) = V(a).

Здесь точка а рассматривается как промежуток (отрезок)

/ = [а, а].

Финансовый поток, задаваемый величиной V, будем называть дискретным, если он имеет дискретное (конечное или бесконечное) множество особых точек av а2,..., ап,... таких, что для любого промежутка У, не содержащего ни одной особой'точки, соответствующее значение величины потока Кравно нулю:

V(J) = 0.

В этом случае совокупность особых точек называется носителем общего потока. Совершенно ясно, что дискретный поток с множеством особых точек а,,..., а , п <<» — обычный поток событий (поток 1-го рода), описанный выше. Действительно, если положить tk ~ ак wCk V{ak), то получим поток событий

с/,={(/,,с1),(/1,с2),...,(/.,с,)}, «<~,

причем, как легко видеть, нетто-значение потока CF на любом промежутке /совпадает со значением величины /исходного дискретного потока:

NV(CF, J) = V(J).

Последнее равенство, в свою очередь, подсказывает, как для обычного (дискретного) потока событий задать соответствующий ему общий поток, определяемый величиной V.

Вернемся теперь к общим потокам CF, задаваемым величиной V. Пусть / — произвольный промежуток (любого вида) с концами а и Ь. Обозначим его как/ = < а, Ь>. Назовем средней плотностью потока на промежутке / величину

где |/| = Ь — а — длина промежутка /. Будем говорить, что поток имеет конечную плотность fx(c) в точке с, если существует предел

Таким образом, плотность /і(с) в точке с есть предел средней плотности потока по промежуткам, содержащим с (с є J), при условии, что их длина стремится к нулю (|/| —» 0). Существование конечной плотности в точке с означает, что для достаточно малых (по длине) промежутков /имеет место приближенное равенство

к(/)-м(с)И=/і(с)(*-в),

которое тем точнее, чем меньше длина промежутка /. В частности, отсюда следует, что V(J) —> 0 при |у| —> 0, с є J, или, как еще говорят,

поток непрерывен в точке с, т.е. значение потока V({с}) в этой точке равно нулю:

к(И)=о.

Поток, непрерывный в каждой точке сє Т, называется (всюду) непрерывным.

Для непрерывного потока значение величины V на промежутке /= < й, Ь> не зависит от #ид<я промежутка:

V(a, Ь) = b]) V([a, Ь)) = А)).

Поэтому величину непрерывного потока можно рассматривать не как функцию промежутка, а как обычную функцию двух переменных (концов промежутка):

V(J)=V(a,b). Так в дальнейшем и будем поступать.

Условие аддитивности в этом случае запишется в виде

V(a, с) = V(a, b) + V(b, с)

для a<b<c.

В частности, плотность непрерывного потока в точке есть предел

ц(с)= lim —^ -, х<с<у.

г v ! (у-х}-»« у-х

Особое значение в дальнейшем будут играть потоки с кусочно-непрерывной плотностью }і(х) в любой точке из Т. Такие потоки назовем абсолютно непрерывными.

В математическом анализе показывается, что аддитивная функция V с кусочно-непрерывной плотностью представляется в виде определенного интеграла:

J

в частности,

K([e,6]) = J/i(jt)dx.

а

Этот факт доказывается просто, если определить функцию

Щ1) г V(t0, t),

где tQ — фиксировано. Тогда из аддитивности V и существования плотности немедленно следует

ЛГ(г) = А|(г).

В самом деле

М (t) = lim—і * ^ =

= ВтУ(у+*)-км=|апМ

Таким образом, Л/(/) есть первообразная для i{f). Если — кусочно-непрерывна, то по формуле Ньютона — Лейбница [23] имеем, что

и

{t)At=M{tl)-M{tx),

t,

и, используя снова аддитивность К, получим окончательно

h

Непрерывный поток однозначно задается своей плотностью. Так, взяв в качестве плотности постоянную функцию

/л[х) = сconst,

получим так называемый равномерный поток, который каждому промежутку У длины Г сопоставляет значение

V{J) = cT.

Используя непрерывные и дискретные потоки, можно образовывать смешанные потоки, которые являются суммами потоков с непрерывными и дискретными слагаемыми. В дальнейшем мы будем неоднократно сталкиваться с финансовыми потоками различных видов.

В заключение обратимся снова к общим потокам, задаваемым произвольной аддитивной функцией промежутка К Теория таких функций достаточно сложна, и здесь не будем заниматься ее изложением. Заметим только, что во всех практически интересных случаях можно считать, что функция У, задающая величину потока, разлагается в сумму

V = v[s) + v[c)

дискретной V(s) и непрерывной У(с) частей с конечной плотностью fi(t). Дискретная часть V(s) представляет собой дискретный поток

CF[s)={C(t) eT},

платежная функция которого определяется как значение У в точках ї, представляющих собой вырожденные отрезки {/} = г]. Таким образом,

C('hV ([/,/]).

Естественно, носитель этого потока

£ = suppC^ = {г |С(/)*0}

есть дискретное множество. Отсюда следует, что для любого конечного промежутка / число ненулевых (критических) точек потока конечно, и, следовательно, значение дискретной части потока на этом промежутке можно представить в виде суммы

K<'V) = IC(r).

Непрерывная часть V(c) задается плотностью jii(t), являющейся интегрируемой, например кусочно-непрерывной функцией. В этом случае для любого конечного промежутка / значение непрерывной части V{c) для этого промежутка задается равенством

к'"(у)=/л(/)а/.

J

Таким образом, значения исходного потока определяются «платежной функцией» C(t) дискретной V{s) и плотностью jA(t) непрерывной У{с) частей.

Итак, для любого конечного промежутка J имеем

r(-0=Xc(/)+JP(/)d/.

ге/ J

Последняя формула дает представление для значений общих потоков. Она позволяет работать с общими потоками, сводя действия (преобразования) этих потоков к соответствующим преобразованиям дискретной и непрерывной частей потоков. Естественно, что на общие потоки очевидным образом можно перенести все определения этой главы и их следствия путем их непосредственного «применения» к дискретной и непрерывной частям общего потока.

1.3. Финансовые операции

Финансовые потоки, рассмотренные в предыдущем параграфе, — основной инструмент при построении математических моделей финансовых операций (сделок, контрактов и т.п.).

Пожалуй, одной из самых простых финансовых сделок является

купля/продажа некоторого товара, например финансового актива. Допустим, некоторое лицо в момент t{ купило некоторый актив по цене Р}

р р и спустя некоторое время в момент г2

1 2 продало его по цене Р2. Если учитывать

только цену покупки и продажи, то

'1 '2 временная диаграмма сделки имеет вид,

РисЛЛ9 как на рис. 1.19.

Здесь знак минус суммы Р означает, что, с точки зрения покупателя, приобретение актива означает расход денежных средств. Таким образом, формально эта сделка опишется потоком

CF= {(/р -Р), (tv Р2)}.

Поток CFназывается представляющим, образующим или порождающим потоком сделки. При этом величина

д/> = р Р

Т 2 1

называется ценовым доходом сделки.

Купив актив, покупатель становится его владельцем на период владения [/р ?2|, который совпадает с периодом самой сделки. Это означает, что владелец (покупатель) может получать текущий доход от актива в течение периода владения. Так, лицо, купившее в начале года акции

некоторой компании и продавшее их в конце года, является владельцем этих акций в течение года и, следовательно, имеет право на

получение дивидендов. Аналогичным образом лицо, купившее облигации, имеет право на получение процентов (купонов) по ним и т.д. Даже

покупатель (владелец) реальных активов, например недвижимости,

транспортных средств и т.д., может получать текущий доход в виде арендной ~Pl,--—— ®j — р*

платы. Учитывая возможность получе ' 1

ния текущего дохода, диаграмму сдел- /t J t2

ки купля/продажа можно изобразить Рис j 20

так, как на рис. 1.20. Здесь Dd— величина текущего дохода от актива за период /. Таким образом, формально описываемую сделку можно описать парой потоков: потоком событий (потоком 1-го рода)

CFX = -Р), (Г2, Р2)}

и потоком 2-го рода

CF2 = {(/,/>)},

где /=[/,, f2) — период сделки; D— Df = DT — текущий доход за период сделки длины |/| = Г= /2 /г

Итак, владелец актива получит два вида дохода: ценовой

АР = Р -Р

и текущий — Dr В сумме эти доходы дают так называемый полный доход

IT=DT+ АРТ.

Например, лицо, купившее акцию в начале года по цене Р = ?л 60, продавшее ее в конце года по цене Р2 = рл 80 и получившее дивиденды в размере 5, получит полный доход /= 80 60 + 5 = 25(3?).

Конечно, на практике текущий доход (например, дивиденды) выплачивается либо отдельным платежом, либо серией таких платежей. Например, дивиденды по акциям могут выплачиваться одним платежом в конце года. В западной практике нередки выплаты дивидендов ежеквартально. Выплата текущего дохода одним платежом или серией платежей с формальной точки зрения означает актуализацию интервального потока

CF2={(J,D)}.

Если, например, доход выплачен одним платежом в конце периода У, то имеет место финализация, т.е. поток CFi преобразуется в поток

1_Г0Р°Да CF2 = FmCF2={(t2iD)},

р р +D состоящий из одного события (tr /)),

11 2( представляющего выплату текущего дохода D в момент tT В результате диаг^ f2 рамма такой операции приобретет вид,

Рис121 как на рис. 1.21.

По существу, это означает, что с формальной точки зрения учет текущего дохода (с заданной схемой выплат) позволяет описывать сделку не парой разнородных потоков CF] и CF2, а одним потоком (1 -го рода) CF, который представляет собой сумму

CF = CFl + CF2

ценового потока CFj и преобразованного потока доходов CFr

Так, для приведенного выше примера покупки акции по ;#60, продажи по .#80 и получении дивидендов в конце года в размере № 5, представляющий сделку поток имеет вид

CF= {(0,-60), (1,85)}.

Поэтому на практике при анализе финансовых операций связанные с ними денежные потоки доходов не всегда тщательно разделяются на «ценовые» и «текущие».

Часто в качестве представляющего сделку потока берется некоторый «агрегированный» или «образующий поток», отдельные элементы которого включают как ценовые, так и текущие (доходные) компоненты. Так, при погашении кредита в рассрочку отдельные погасительные платежи могут включать как выплату процентов, так и частичные погашения основного долга.

Рассмотрим, например, простейшую кредитную сделку, которая будет подробно изучаться в гл. 2. В этой сделке кредитор выдает в момент t{ должнику кредит на сумму Р — основной долг, при этом

должник возвращает в момент t2 долг

_р / р (т.е. Р) и оплачивает предоставленный

кредит суммой /, представляющей со^—— бой величину процентов за период сдел1 J 2 киг Диаграмма простой кредитной сделРис. 1.22 ки изображена на рис. 1.22.

Знак минус при сумме Р в момент t0 означает, что сделка описывается с тонки зрения кредитора, для которого выдача кредита представляет собой расход собственных денежных средств.

Таким образом, как и в случае купли/продажи, простая кредитная сделка описывается парой потоков: потоком (1-го рода)

CF^{(t0J-P),(trP)}

и потоком (2-го рода)

В простой кредитной сделке проценты выплачиваются обычно единовременно в конце или в начале периода. В первом случае процентный поток CF2 преобразуется в поток

CF2 = FinCF={{t[,I)}, а образующий (представляющий) поток CFсделки примет вид

CF= CF{ + CF2 = {(t0, -/>), (г,, P+ /)}.

Суммам, выплачиваемая в момент t] (дата погашения), называется в этом случае полной суммой долга или суммой погашения.

Во втором случае процентный поток CF2 преобразуется в поток

CF2 = AdvCF7 = {(tuJ)},

а образующий поток сделки примет вид

CF=CFl + CF2 = {(tQ,-P+I),(tvP)}.

Здесь PQ — Р I — выданная сумма кредита, равная основной сумме долга, уменьшенной на величину выплачиваемых процентов.

Рассмотрим, например, простую кредитную сделку с основной суммой долга Р~ .-#1000 сроком в один год и величиной процентов / = М 1 00. При выплате процентов в конце года поток платежей имеет вид

СЛ,= {(0,-1000),(1, 1100)},

а в случае выплаты процентов авансом, т.е. в начале года, поток платежей представляется в виде

CF= {(0,-900), (1, 1000)}.

Таким образом, в простейших сделках реальные потоки платежей сводятся к двум событиям: начальному и конечному, которые можно рассматривать с точки зрения одного из контрагентов сделки как

4-5169

расход и приход денежных средств соответственно. При этом в обычной ситуации (но не всегда!) расход предшествует приходу.

Лицо, с точки зрения которого в дальнейшем будут описываться сделки, назовем (условно) инвестором. В случае простой сделки начальное событие (расход) представляет собой инвестирование (покупку актива, выдачу кредита) на определенный период времени (инвестиционный период) с целью получения инвестиционного дохода (как текущего, так и ценового). При выбранной схеме выплаты текущего дохода (актуализации «доходного» потока) простейшая финансовая сделка с формальной точки зрения будет представлена потоком

CF={(tl,Cl),(t2, С2)}.

Здесь величины платежей Сх и С2 могут иметь любой знак. В наиболее распространенном случае С{ < 0 и С2 > 0.

Конечно, на практике встречаются не только простейшие сделки, сводящиеся к двум суммам (событиям). Во многих сделках участвуют серии платежей. Так, выданный кредит может погашаться не единым платежом, а в рассрочку, т.е. серией погасительных платежей. Кроме того, сам кредит может быть выдан не единовременно, а также серией платежей (траншей), например, при представлении так называемой кредитной линии. Наконец, сложные инвестиционные операции, такие, как управление портфелем активов (финансовых или реальных), могут включать весьма большое число элементов: покупку и продажу составляющих портфель активов, аккумуляцию текущего дохода, его выплату или реинвестирование и т.д. Например, пенсионный фонд аккумулирует взносы участников, инвестирует их в различные активы, управляет ими, осуществляет пенсионные выплаты и т.д.

Во многих случаях сделки, осуществляемые как отдельными физическими, так и юридическими лицами (финансовыми институтами), можно описать представляющими эти сделки финансовыми потоками. При этом в детальном описании могут отдельно фигурировать как ценовые (капитальные) потоки, представляющие «последовательные состояния» счета, связанного с реализацией сделки, так и доходные (текущие) потоки, представляющие потоки доходов, полученные от ее активов. В конечном счете актуализация этих потоков позволяет описывать сделки в виде одного потока событий (платежей), полностью представляющего все денежные суммы, участвующие в сделке. Такие потоки назваются представляющими (образующими или порождающими) связанные с ними сделки. В таком описании сделки до некоторой степени маскируется различное происхождение денежных сумм, поскольку в одной сумме (событии) представляющего потока может учитываться как (ценовая) капитальная, так и доходная составляющие. Хотя отмеченное выше различие исчезает, тем не менее остается еще один аспект дела, позволяющий различать отдельные платежи представляющего потока. Он заключается в знаках денежных сумм, составляющих события, представляющие сделку потока. Корректное описание сделки обычно предполагает выбор определенной ориентации денежных сумм, участвующих в сделке. Обычно эта ориентация выбирается в соответствии с выбранной точкой зрения, например, инвестора, реализующего сделку, финансового института и т.д. Выбор такой точки зрения классифицирует денежные суммы потока либо как отток средств (расходы, инвестирование, оплата и т.д.), либо как их приток (выручка от продажи, получение дохода, поступление взносов и платежей и т.д.).

Таким образом, общую финансовую операцию можно представить парой потоков платежей: расходного

CF-q),{q,c-),...,{t;,с;)}

и приходного

CF^{(t;,c:),{t;,q),...,{cc;,)}.

Расходный поток для некоторых видов сделок назовем также исходным или открывающим сделку и соответственно приходный поток — заключительным или завершающим. Кроме того, в специальных сделках эти потоки могут иметь и другие специфические названия, связанные с типом сделки. Так, в кредитных сделках исходный поток состоит из предоставляемых кредитных сумм, и его называют кредитным или ссудным потоком. Соответственно заключительный поток является потоком погасительных платежей или, коротко, потоком погашения (погасительным потоком).

В сумме исходный и заключительный потоки сделки дают представляющий поток

CF = CF+ CF

Например, для обобщенных кредитных сделок, рассматриваемых в гл.5 и 13, исходный (кредитный) поток сводится к единственному платежу — выдаче кредита. В этом случае

CF-={(!,-Р)},

где /о — момент (дата) выдачи кредита; Р — начальная сумма долга.

Кредит погашается серией погасительных платежей, образующих заключительный поток

c/^={(/1,q),(/2,co,...4,c.)}, '„'2,...л»„>

т.е. поток погасительных платежей.

Описание сделки представляющим ее потоком платежей является удобным и строгим с формальной точки зрения. Все другие характеристики сделки, такие, как чистый доход, доходность, процентная ставка, как правило, однозначно определяются ее потоком.

Конечно, на практике порядок задания временных, финансовых и других параметров сделки зависит от конкретных особенностей описания сделки. Так, в обобщенных кредитных сделках могут в качестве исходных параметров задаваться сумма выданного кредита Р, срок сделки Т, процентная ставка по кредиту и схема погашения. В этом случае погасительные платежи определяются (вычисляются) по исходным данным. В конечном счете завершение сделки предполагает выплату всех сумм, предписанных условиями сделки. Сточки зрения, например, бухгалтера, собственно только эти платежи и существенны, тогда как другие параметры (например, процентная ставка) являются лишь дополнительными характеристиками сделки.

Для сложных финансовых операций, например таких, как управление портфелем активов, включающим огромное количество элементарных составляющих сделок, таких как купля/продажа активов, реинвестирование полученного дохода и т.п., важнейшей характеристикой финансовой эффективности сделок, с точки зрения инвестора, является накопленный в результате этих сделок инвестиционный капитал. Собственно проведение различных сделок преследует главную цель инвестора — добиться максимального роста инвестированного капитала. При этом, хотя каждая отдельная сделка, как правило, имеет конкретный период (срок сделки), их последовательность, реализуемая инвестором с целью увеличения капитала, обычно не имеет заранее заданного конечного срока. С этой точки зрения инвестирование капитала можно рассматривать как потенциально бесконечный во времени инвестиционный или финансовый процесс.