10.1. характеристики портфеля ценных бумаг

10.1. характеристики портфеля ценных бумаг

Предположим, что портфель составлен из я-го числа различных видов ценных бумаг. Доходность каждой ценной бумаги является случайной величиной. Пусть Xj — доля в общем вложении, приходящаяся на у-й вид ценных бумаг, — подчиняется соотношению

п

е*/=1 (ЮЛ)

Ожидаемая доходность (эффективность) а} у-й ценной бумаги, входящей в портфель, является математическим ожиданием ее доходности. Ожидаемая доходность портфеля, являющаяся математическим ожиданием суммарной доходности входящих в портфель ценных бумаг, вычисляется по формуле

п

ap = Hxjaj(10.2)

7=1

Дисперсия доходности портфеля определяется соотношением

gp = zz w^' (Ю.З)

где ay — ковариация случайных доходностей /-й и у-й ценных бумаг, вычисляемая по формуле

а„ = E{(Ai ad(Aj а,)},

где E — оператор математического ожидания;

Д, Aj — случайные доходности i-й и у-й ценных бумаг соответственно.

Рассмотрим величину риска портфеля при различных значениях корреляционных связей между доходностямй ценных бумаг, входящих в портфель.

Предположим, что эффективности различных ценных бумаг не коррелированы, т.е. а/У = 0 при і * j. Тогда формула для расчета ковари-ации принимает вид

=E{(AJ-ajf} = aJТаким образом, если а0 = 0 при / *у, Td ковариация у-й ценной бумаги равна ее дисперсии. В этом случае формулу для дисперсий доходности портфеля ценных бумаг (10.3) можно записать в виде

7=1

Если деньги вложены в ценные бумаги равными частями, т.е. Xj — то формулы (10.2), (10.4) приобретают вид

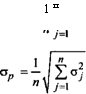
(10.5)

Рассмотрим возможность уменьшения риска снижения доходности за счет диверсификации (разнообразия) портфеля. Если в правую часть соотношения (10.5) вместо всех g2подставить максимальное значение дисперсии а^ах из всего набора дисперсий с2-; то получим неравенство

а <^L, ,(10.6)'

так как правая часть соотношения (10.5) в Этом случае имеет іид

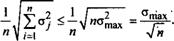
Из выражения (10.6) следует, что при увеличении числа ввдор ценных бумаг п риск портфеля уменьшается й стремится к нул^о т|рц п -> оо. Это так называемый эффект диверсификации портфеля.

Для анализа влияния корреляции на величину риска портфеля ценных бумаг в формуле для дисперсии доходности (10.3) выразим ковариацию случайных доходностей через коэффициент корреляции

У

Pij= 

Тогда (10.3) можно представить в виде

2 П "

°р =ZZ(artXoy^/)P,y.

/=17=1

(ЮЛ)

(10.8)

так как при суммировании по любой переменной получим один и тот же результат.

Если деньги вложены в ценные бумаги равными частями, т.е. Xj = то

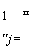1

2>у

v/='

Отсюда следует, что стандартное отклонение портфеля находится в интервале ,

^min — &р — Отах.

Таким образом, риск портфеля будет иметь тот же порядок, что й риски отдельных ценных бумаг, т.е. диверсификация не дает положительного эффекта.

При pij = —1 рассмотрим риск портфеля, состоящего из двух видов ценных бумаг (и = 2). Для і = j выражение (10.7) принимает вид

Pjj =

aj°j

А.

(Ю.9)

Подставив (10.9) в (10.8), получим

/=іу=і

= ajxf + <sx -2axx\<s2x2 = (с*!*, -o2x2)2.

(10.10)

Из выражения (10.10) следует, что при полной обратной корреляции дисперсия доходности портфеля может быть равна нулю, т.е. риск отсутствует. Это имеет место при выполнении соотношения

а{Х = а2х2. (10.11)

Состав такого портфеля можно определить, решив систему из уравнения (10.11) и уравнения для долей портфеля (10.1):

^Х2=0. <*1

х + х2 = 1» *1

Решения данной системы имеют вид

Х =

х2 =

°2І*

+ g2/gi

1 + а2/а1

1

10.2. Портфель из двух видов ценных бумаг

Для каждого портфеля на графике зависимости ожидаемой доходности от стандартного отклонения можно построить точку, рассчитанную по формулам (10.1)—(10.3). Рассмотрим частный случай инвестиционного портфеля, состоящего из двух видов ценных бумаг. Пусть в инвестиционном портфеле доля ценных бумаг первого вида равна х, а бумаг второго вида равна 1-х. Математические ожидания доходностей ценных бумаг первого и второго видов, их дисперсии и ковариацию обозначим через al9a2,<j2 9а2,а12. Тогда (10.2) и (10.3) можно записать в виде

ар ~ ха + (1 х)а2,

(10.12)

а2р = х2о2 +(х)2 о2 + 2х( х)с{ 2.

Найдем точку, в которой производная функции ар(ар) стремится к бесконечности. Функция (10.12) задана параметрически как ар(х) и ср(х). Поэтому

dap dap/dx 2(ах -а2)ор

dcP dcP /Л 2ха + 2(1" х)2 «г + 2(1 jc х)сх 2 Искомая точка находится из уравнения

x0a?+(l-x0)2a^+(t-2x0)a12 =0. (10.13)

Решая уравнение (10*13) относительно яь, получим

g2 -q12

g +О2 ~20|2

(10.14)

Решение. Рассмотрим пример 1. Определим точку экстремума по формуле (10.14):

0,45 + 0,9 Составим таблицу (табл. 10.2).

Таблица 10.2

0 0,250 0,150 0,130 0,949 0,731

0,500 0,110 0,581 0,667 0,097 0,548

0,750 1,000 0,090 0,070 0,556 0,671

0,2 0,4 0,6 0,8

Стандартное отклонение

Рис. 10.1. График функции ар(ар)

Эта кривая имеет вид «пули». ар = 0,548 — минимальное из всех возможных среднеквадратических отклонений, т.е. риск будет минимальным для структуры портфеля с долей бумаг первого вида jc = 0,667 и долей бумаг второго вида 1 — х = 0,333. При этом ожидаемая доходность ар = 9,664\%.

Для примера 2 соотношения (10.12) можно записать в виде ар =xa,+(l-x)a2,l

<V=0-*)<*2J Определим производную:

dap ^ dap/dx _ а2-ах

dcP dop/d* G2

Так как производная — величина постоянная, то исследуемая функция является отрезком прямой линии. Для х = 1 имеем ар ~ О] и ар — 0. Если заданы точка, лежащая на прямой, и угловой коэффициент, то прямая определена, и ее уравнение имеет вид

аР =а +——Lv

Подставив в него исходные данные примера, получим искомую функцию:

aD =0,07 + 0,15"0,07ор = 0,07 + 0,08433о„.

р Р Р

Отрезок прямой легко построить по двум точкам. Одна точка определена. Ее координаты (0; 0,07). Координаты второй точки находятся при х = 0. В этом случае ар = а2, ср = ст2. Тоща координаты второй точки (0,15; 0,949). На рис. 10.1 искомая функция представлена в виде левого отрезка прямой линии.

На рис. 10.1 также представлены графики других примеров табл. 10.1. Стрелка указывает направление возрастания ковариации ценных бумаг первого и второго видов.

Для примера 6 из условия р|2 = 1 следует, что а!2 = а,а2. Тогда уравнения (10.12) можно записать в виде

ар =хах + {-х)аъ ) ор =х(ах-с2) + а2.

Найдем производную:

dQp _ а ~ ^2 dop а, -а2

Так как данная производная не зависит от стандартного отклонения портфеля, то искомая функция является отрезком прямой линии, соединяющим точки, координаты которых находятся из условий:

при jc = 1 имеем ар = а\ ор — ои

при jc = 0 имеем ар = а2 ор = а2.

Для условий примера первая точка имеет координаты (0,671; 0,07), а вторая — координаты (0,949; 0,15). На рис. 10.1 искомая функция изображена в виде правого отрезка прямой. ►

Как следует из приведенных примеров, вид функции ар(ор) существенным образом зависит от ковариации доходностей ценных бумаг. При увеличении ковариации риск (стандартное отклонение) при той же доходности возрастает.