10.3. оптимальный портфель
10.3. оптимальный портфель
Ожидаемая доходность портфеля (10.2) и дисперсия его доходности (10.3) зависят от структуры портфеля, т.е. от видов ценных бумаг и их доли в общем вложении. Можно построить оптимальный портфель, минимизирующий риск при определенных условиях. Этого можно достичь, например, минимизируя дисперсию (10.3) при фиксированном уровне доходности (10.2) и нормировании весовых коэффициентов (10.1). Такое решение минимизации риска впервые рассмотрено Марковицем. Математическая формулировка задачи имеет вид
• mm
(10.15)
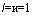 | |||
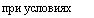 | |||
2Zxjaj-aP=°> 1>,-1 = 0.
(10.16)
Поиск оптимального решения осуществляется методом множителей Лагранжа. Функция Лагранжа для условий (10.16) имеет вид
| п п L = HHxixjcij | п | („ ^ | |
| 1LxJaj -Op | + n | ||
| 0=i ) | |||
(10.17)
Оптимальный портфель находится из решения относительно xj9 к и |i системы линейных уравнений
(10.18)
:0.
dL dL dL
dxj дк ді
Для трех видов ценных бумаг функция Лагранжа приобретает вид
L = xfcu + х2с22 + X3O33 + 2х,х2о12 + 2х1х3о13 + 2х2х3о23 + +X^jcjai + х2а2 + х3д3 -ар)*-)*.^ +jc2 + х3 -1).
Отсюда находим систему линейных уравнений (10.18) при условии Gij = Gjf.
EL
dL
dx2
dL
дхъ
dL
дк'
dL
dp"
:^xa\ +2x2Gj2 +2jc3Gi3 +ajX, + |i = 0; = 2jciG2i + 2x2a22 + 2x3a23 + a2k + ц = 0; = 2jcia3i + 2x2G32 + 2X3G33 + a^k + ц = 0;
xa + x2a2 + ВД+0-иО'Ц = ^;
x + x2 + x3 +0-и0'Ц = 1.
(10.19)
Данная система из пяти линейных уравнений с пятью неизвестными может быть решена, например, методом Крамера. Ее решение для принятого состава портфеля из трех видов ценных бумаг имеет вид
х °1 . х °2 .
х
(10.20)
где х, — доход от вложенных в портфель средств на приобритение бумаг первого вида;
х2 — доход от вложенных в портфель средств на приобретение бумаг второго вида;
х3 — доход от вложенных в портфель средств на приобретение бумаг третьего вида.
 При вычислении определителя D = Ьу п-то порядка его можно разложить на сумму произведений всех элементов какой-либо строки (или столбца), умноженных на соответствующие им алгебраические дополнения, по формуле
При вычислении определителя D = Ьу п-то порядка его можно разложить на сумму произведений всех элементов какой-либо строки (или столбца), умноженных на соответствующие им алгебраические дополнения, по формуле
1=1 ы
где by — элемент /-й строки (столбца) и у-го столбца (строки);
Щ — минор порядка п — 1, получающийся из D вычеркиванием /-й строки (столбца) и у-го столбца (строки); By — алгебраическое дополнение.
Из графика функции ар(ар) примера 10.1 (см. рис. 10.1) следует, что возможно существование экстремальной точки, в которой стандартное отклонение (дисперсия) портфеля имеет минимальное значение. Эту задачу можно решить с помощью метода множителей Лагранжа:
п п
gp = z z xixjcij min
/=1У=1
при „
Целевая функция Лагранжа для этого условия имеет вид
п п п
l = z z xixj°ij+1* z *j -1
Координаты экстремальной точки Х/ находятся из системы линейных уравнений
dL = dL = dxj Эц
Функция Лагранжа для трех видов ценных бумаг принимает вид
L = X] С| j + *2**22 х3^33 2хХ2&2 + ^хх3^3 ^Х2Х3®23 + ц(х,+х2+л:3-1).
Отсюда находим систему линейных уравнений относительно х,, х2, х3 и ц:
— = 2х,а,, + 2х2а12 + 2х3а13 + р = 0;
= 2*1 а2і + 2х2а22 + 2дг3а23 + ц = 0;
йх2
= 2лГ|азі + 2jc2a32 + 2jc3o33 + ц = 0;
йх3
— = Х| + х2 + х3 + 0р = 1. 3|д
Эта точка является исходной при анализе доходности и риска портфеля ценных бумаг. После ее определения инвестору будет известна ожидаемая доходность при минимально возможном риске. Так как в указанной точке доходность растет значительно быстрее, чем стандартное отклонение, то инвестор имеет возможность изменить состав портфеля так, что ожидаемая доходность может заметно увеличиться при незначительном увеличении риска. При этом необходимо иметь в виду, что изменение состава портфеля на заданную величину стандартного отклонения может как увеличить, так и уменьшить ожидаемую доходность.
Метод выбора оптимального состава портфеля можно свести к следующему. Выбрав вид ценных бумаг, инвестор рассчитывает состав портфеля для минимально возможной дисперсии. Затем рассчитываются минимально возможное стандартное отклонение и соответствующая ему ожидаемая доходность. Если инвестор предпочитает повысить ожидаемую доходность, то он для ряда новых доходностей определяет стандартное отклонение по приведенной выше методике Марковича и выбирает приемлемый для себя вариант.
Приведенную оптимизацию портфеля ценных бумаг удобно проводить в матричной форме.
Характеристики рисковых ценных бумаг задаются матрицей кова-риаций

(10.21)
матрицей-столбцом ожидаемых доходностей я, матрицей-столбцом неизвестных долей х и единичной матрицей-столбцом /:
| «1 | " 1 " | ||||
| *2 | • | ||||
| аУ | *У | ; /=[!] = | Ї | ||
| У. |
(10.22)

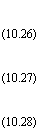 о р — х ах
о р — х ах
при двух 'Ограничивающих условиях
&х-ар=0; /'х-Л = 0. Тогда функция Лагранжа (10.17) принимает вид
L хрх + Ца'х -ар) + i(I'x -4).
Оптимальный портфель находится из решения относительно х} системы линейных уравнений (10.18). Продифференцировав (10.28)
по л?; X и iv получим
2ох + Ал + ц/ = 0;
ах = ап
/5с = 1.
Раскрыв данную систему, находим:
2сТ] | jc| + 2oi2jc2 + ... + 2g|wjcw + аХ + і = 0; 2a2|Xi + 2o22x2 + ... + 2o2/rx/J + a2A, + p. = 0;
2<tw|JC| + 2aw2x2 +... + 2annxn + anX + i = 0; + a2*2 + ... + яя*я +0'U0'[i = a/?; *! + x2+...+ x„+O«U0'H = l.
(10.29)
Ранее систему линейных уравнений (10.29) мы решали отностиель-но Xj методом Крамера. Иначе ее можно записать в матричном виде:
| 2о„ | 2о,2 . | •• 2о,„ | «1 | 1 | хх | |
| 2о21 | 2<Т22 • | •• 2о2„ | а2 | 1 | х2 | |
| 2о„, | 2о'и2 '. | .. 2о„„ | о„ | Г | * | хп |
| <* | °2 • | 0 | 0 | X | ||
| 1 | 1 | 1 | 0 | 0 | ц |
1
(10.30)
Обозначим матрицу риск-доходности через А, вектор [xj, X, ц] — через X, а вектор правой части уравнения — через В. Тогда уравнение (10.30) можно записать в виде
АХ = В.
(10.31)
Решая (10.31), получим формулу для определения неизвестных долей каждого вида рисковых ценных бумаг в оптимальном портфеле:
Х=АХВ,
(10.32)
где матрица-столбец
матрица риск-доходности
В =
0 0
| 2оп | 2о12 .. | • 2о,„ | ^1 | 1 |
| 2о2| | 2о22 • | .. 2о2и | а2 | 1 |
| 2ои2 • | •• 2о„„ | а» | 1 | |
| а | а2 . | «и | О | 0 |
| 1 | 1 | 1 | 0 | 0 |
а А 1 — матрица, обратная матрице А.
Обратной по отношению к матрице А = [а„] называется матрица
Л"1 = С = [<-] =
и
Т т где 4у — алгебраическое дополнение элемента а7у в определителе транспонированной матрицы АТ, т.е. умноженный на (— минор, полученный из АТ вычеркиванием /-й строки и у-го столбца.
При определении минимально возможного значения дисперсии портфеля система уравнений (10.29) принимает вид
^G\x +2<*i2*2 +—+20|яхя + ц = 0; 2а2Х + 2о22х2 + — + 2а2пхп + Ц = Ф
2оя|Хі+2оя2^+... + 2оІшхи + Ц = 0; JCj + jc2+...+ хя + 0«п. = 1.
(10.33)
Перепишем систему уравнений (10.33) в матричной форме:
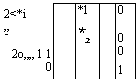 |
1
2o«i 2о„2
1
(10.34)
Обозначим матрицу риска через а, вектор [*,, ц] — через х, а вектор правой части — через р. Тогда систему уравнений (10.34) можно записать в виде
ах= РРешение уравнения (10.35) имеет вид
Х=а-'р,
где а"1 — матрица, обратная матрице а.
(10.35) (10.36)
Обсуждение Финансовый менеджмент
Комментарии, рецензии и отзывы
